目录
前言
六、批量数据组织——数组
6.4 线性表——分类与检索
6.4.1 主元排序
6.4.2 冒泡排序
6.4.3 插入排序
6.4.4 顺序检索(线性搜索)
6.4.5 对半检索(二分查找)
算法比较
前言
线性表是一种常见的数据结构,用于存储一组具有相同类型的元素。本文主要介绍了下面几种常见的线性表的排序和检索算法:
-
主元排序(主元选择排序):这是一种选择排序算法,它通过选择主元(通常是最小或最大元素)并将其放置在正确的位置来进行排序。该算法重复选择主元并移动它,直到所有元素都有序排列。
-
冒泡排序:这是一种简单的排序算法,它通过多次比较和交换相邻元素的方式将较大的元素逐渐向右移动。通过重复这个过程直到所有元素都有序排列,最终实现排序。
-
插入排序:这是一种通过将元素逐个插入已排序序列的合适位置来完成排序的算法。在插入排序过程中,将当前元素与已排序序列中的元素逐个比较,直到找到合适的插入位置。
-
顺序检索:也称为线性搜索,是一种简单直接的搜索方法,从线性表的起始位置开始逐个比较元素,直到找到目标元素或遍历完整个线性表。
-
对半检索(二分查找):对于已排序的线性表,可以使用对半检索来提高搜索效率。该算法通过将目标元素与线性表的中间元素进行比较,然后根据比较结果将搜索范围缩小一半。重复这个过程,直到找到目标元素或确定目标元素不存在。
六、批量数据组织——数组
6.4 线性表——分类与检索
6.4.1 主元排序
主元排序(主元选择排序)是一种简单的排序算法,它通过选择线性表中的主元(也称为枢轴元素)并将其放置在正确的位置上来实现排序。主元排序算法的基本思想是:选择一个主元,将线性表中小于主元的元素放在主元的左边,将大于主元的元素放在主元的右边,然后对主元的左右两部分递归地进行排序,直到整个线性表有序。
void mainElementSort(int arr[], int left, int right) {
if (left < right) {
int pivot = partition(arr, left, right); // 获取主元的位置
mainElementSort(arr, left, pivot - 1); // 对主元左边的元素进行排序
mainElementSort(arr, pivot + 1, right); // 对主元右边的元素进行排序
}
}
int partition(int arr[], int left, int right) {
int pivotIndex = left; // 将第一个元素作为主元
int pivotValue = arr[left];
int i, j;
for (i = left + 1; i <= right; i++) {
if (arr[i] < pivotValue) {
pivotIndex++;
swap(arr, i, pivotIndex); // 将小于主元的元素交换到主元的左边
}
}
swap(arr, left, pivotIndex); // 将主元放置在正确的位置上
return pivotIndex;
}
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}在主元排序算法中,首先选择一个主元,这里选择线性表的第一个元素作为主元。然后,从主元的下一个位置开始遍历线性表,将小于主元的元素逐个交换到主元的左边,并记录交换次数。最后,将主元放置在正确的位置上,即交换次数加一的位置。这样,主元左边的元素都小于主元,主元右边的元素都大于主元。
接下来,对主元的左右两部分分别递归地应用主元排序算法,直到每个子序列只有一个元素为止。最终,整个线性表就会被排序。
主元排序是一种简单但有效的排序算法,其平均时间复杂度为O(nlogn),其中n是线性表的长度。然而,如果每次选择的主元都不合理,可能导致算法的性能下降。因此,在实际应用中,选择合适的主元策略对算法的性能至关重要。
6.4.2 冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法,它通过反复交换相邻的元素将最大的元素逐步 "冒泡" 到数组的末尾,从而实现排序。冒泡排序算法的基本思想是:比较相邻的两个元素,如果它们的顺序不正确,则交换它们,直到整个数组有序。
void bubbleSort(int arr[], int n) {
int i, j;
for (i = 0; i < n - 1; i++) { // 通过n-1次循环将最大元素冒泡到末尾
for (j = 0; j < n - 1 - i; j++) { // 每次循环比较相邻的两个元素
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp; // 交换位置,使更大的元素向后移动
}
}
}
}在冒泡排序算法中,外层循环控制冒泡的轮数,内层循环用于比较相邻的两个元素并进行交换。每一轮循环都将最大的元素冒泡到当前未排序部分的末尾。通过n-1次循环,就可以将整个数组排序完成。
冒泡排序的时间复杂度为O(n^2),其中n是数组的长度。尽管冒泡排序的时间复杂度较高,但它的实现较为简单,且在某些情况下可能具有一定的优势。然而,在处理大型数据集时,通常会选择更高效的排序算法。
6.4.3 插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法,它通过构建有序序列,不断将未排序的元素插入到已排序序列中的适当位置,从而实现排序。插入排序算法的基本思想是:将数组分为已排序和未排序两部分,每次从未排序部分取出一个元素,将其插入到已排序部分的正确位置。
void insertionSort(int arr[], int n) {
int i, j, key;
for (i = 1; i < n; i++) {
key = arr[i]; // 从未排序部分取出一个元素
j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j]; // 将比key大的元素向后移动
j--;
}
arr[j + 1] = key; // 将key插入到正确的位置上
}
}在插入排序算法中,将数组分为已排序部分(初始为空)和未排序部分。从未排序部分依次取出元素,将其与已排序部分的元素从右向左进行比较,直到找到合适的位置插入。为了插入元素,需要将比插入元素大的元素向右移动一个位置,为插入元素留出空间。最后,将插入元素放置在正确的位置上,即完成一次插入操作。
通过n-1次循环,就可以将整个数组排序完成。
插入排序的时间复杂度为O(n^2),其中n是数组的长度。尽管插入排序的时间复杂度较高,但它对小型数据集的排序效果较好,并且在部分已经有序的情况下,插入排序的性能会更加出色。
6.4.4 顺序检索(线性搜索)
顺序检索(Sequential Search),也称为线性搜索,是一种简单直观的搜索算法。顺序检索算法的基本思想是:从给定的数据集合中按顺序逐个比较元素,直到找到目标元素或搜索完整个数据集合。
int sequentialSearch(int arr[], int n, int target) {
for (int i = 0; i < n; i++) {
if (arr[i] == target) {
return i; // 找到目标元素,返回元素的索引
}
}
return -1; // 未找到目标元素,返回-1表示失败
}顺序检索算法通过遍历数据集合,逐个比较元素和目标元素是否相等。如果找到了目标元素,就返回该元素在数据集合中的索引;如果遍历完整个数据集合仍未找到目标元素,则返回-1表示搜索失败。
顺序检索的时间复杂度为O(n),其中n是数据集合的大小。由于顺序检索需要逐个比较元素,它的效率较低,特别是在大型数据集合上。然而,在小型数据集合或无序数据集合中进行简单搜索时,顺序检索是一种常用的方法。
6.4.5 对半检索(二分查找)
对半检索(Binary Search),也称为二分查找,是一种高效的搜索算法,用于在有序数组或列表中查找目标元素。对半检索算法的基本思想是:将数组或列表分成两部分,通过比较目标元素与中间元素的大小关系,确定目标元素可能在的那一部分,然后继续在该部分中进行查找,缩小搜索范围,直到找到目标元素或确定目标元素不存在。
int binarySearch(int arr[], int n, int target) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2; // 计算中间元素的索引
if (arr[mid] == target) {
return mid; // 找到目标元素,返回元素的索引
} else if (arr[mid] < target) {
low = mid + 1; // 目标元素在右半部分,调整搜索范围
} else {
high = mid - 1; // 目标元素在左半部分,调整搜索范围
}
}
return -1; // 未找到目标元素,返回-1表示失败
}对半检索算法通过比较目标元素与中间元素的大小关系,将数组或列表分成两部分。如果中间元素等于目标元素,就返回中间元素的索引;如果中间元素小于目标元素,说明目标元素在右半部分,将搜索范围缩小到右半部分;如果中间元素大于目标元素,说明目标元素在左半部分,将搜索范围缩小到左半部分。通过不断缩小搜索范围,最终可以找到目标元素或确定目标元素不存在。
对半检索的前提是数组或列表必须是有序的,因为它利用了有序性质进行二分查找。对半检索的时间复杂度为O(log n),其中n是数组或列表的长度。由于每次都将搜索范围缩小一半,对半检索的效率非常高。
算法比较
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define SIZE 100000
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
int partition(int arr[], int left, int right) {
int pivotIndex = left; // 将第一个元素作为主元
int pivotValue = arr[left];
int i, j;
for (i = left + 1; i <= right; i++) {
if (arr[i] < pivotValue) {
pivotIndex++;
swap(arr, i, pivotIndex); // 将小于主元的元素交换到主元的左边
}
}
swap(arr, left, pivotIndex); // 将主元放置在正确的位置上
return pivotIndex;
}
void primeSort(int arr[], int left, int right) {
if (left < right) {
int pivot = partition(arr, left, right); // 获取主元的位置
primeSort(arr, left, pivot - 1); // 对主元左边的元素进行排序
primeSort(arr, pivot + 1, right); // 对主元右边的元素进行排序
}
}
void bubbleSort(int arr[], int n) {
int i, j;
for (i = 0; i < n - 1; i++) { // 通过n-1次循环将最大元素冒泡到末尾
for (j = 0; j < n - 1 - i; j++) { // 每次循环比较相邻的两个元素
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp; // 交换位置,使更大的元素向后移动
}
}
}
}
void insertionSort(int arr[], int n) {
int i, j, key;
for (i = 1; i < n; i++) {
key = arr[i]; // 从未排序部分取出一个元素
j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j]; // 将比key大的元素向后移动
j--;
}
arr[j + 1] = key; // 将key插入到正确的位置上
}
}
int sequentialSearch(int arr[], int n, int target) {
for (int i = 0; i < n; i++) {
if (arr[i] == target) {
return i; // 找到目标元素,返回元素的索引
}
}
return -1; // 未找到目标元素,返回-1表示失败
}
int binarySearch(int arr[], int n, int target) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2; // 计算中间元素的索引
if (arr[mid] == target) {
return mid; // 找到目标元素,返回元素的索引
} else if (arr[mid] < target) {
low = mid + 1; // 目标元素在右半部分,调整搜索范围
} else {
high = mid - 1; // 目标元素在左半部分,调整搜索范围
}
}
return -1; // 未找到目标元素,返回-1表示失败
}
double measureTime(clock_t start, clock_t end) {
return ((double) (end - start)) / CLOCKS_PER_SEC;
}
int main() {
int arr[SIZE];
// 使用时间作为随机数种子
srand(time(NULL));
// 待排序的数组
for (int i = 0; i < SIZE; i++) {
arr[i] = rand();
};
int n = sizeof(arr) / sizeof(arr[0]); // 数组的长度
int target = 7; // 待搜索的目标元素
// 测量主元排序算法的运行时间
clock_t start = clock();
primeSort(arr, 0, n);
clock_t end = clock();
printf("Prime Sorting Time: %.6f seconds\n", measureTime(start, end));
// 测量冒泡排序算法的运行时间
start = clock();
bubbleSort(arr, n);
end = clock();
printf("Bubble Sort Time: %.6f seconds\n", measureTime(start, end));
// 测量插入排序算法的运行时间
start = clock();
insertionSort(arr, n);
end = clock();
printf("Insertion Sort Time: %.6f seconds\n", measureTime(start, end));
// 测量顺序检索算法的运行时间
start = clock();
int sequentialSearchResult = sequentialSearch(arr, n, target);
end = clock();
printf("Sequential Search Time: %.6f seconds\n", measureTime(start, end));
printf("Sequential Search Result: %d\n", sequentialSearchResult);
// 测量对半检索算法的运行时间
start = clock();
int binarySearchResult = binarySearch(arr, n, target);
end = clock();
printf("Binary Search Time: %.6f seconds\n", measureTime(start, end));
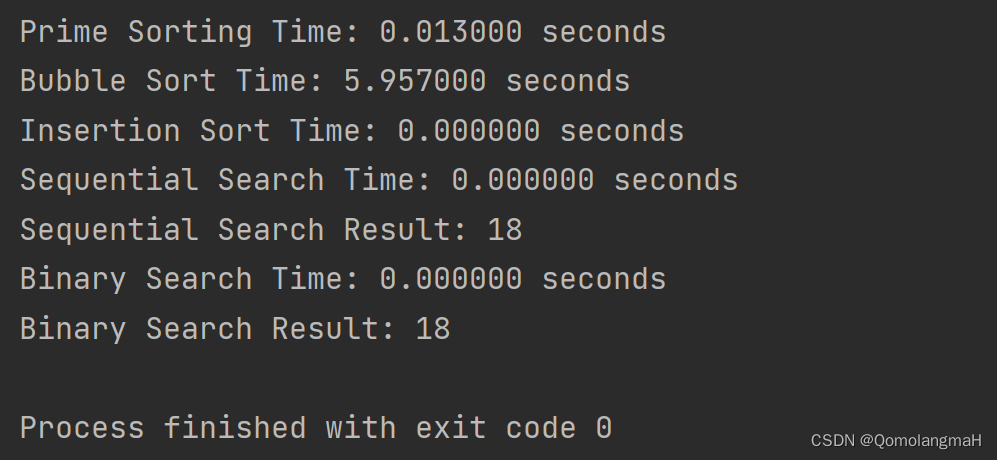
printf("Binary Search Result: %d\n", binarySearchResult);
return 0;
}


![Parse [5/10/2020 7:05:04 PM] with format [yyyy-MM-dd] error!](https://img-blog.csdnimg.cn/51015ccf266d48ebb8adfbf44059eb9b.png)