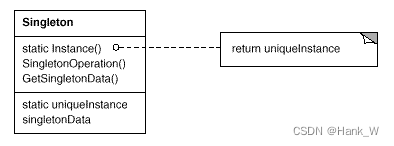
题目

一个正整数的因子是所有可以整除它的正整数。而一个数如果恰好等于除它本身外的因子之和，这个数就称为完数。例如6=1＋2＋3(6的因子是1,2,3)。

现在，你要写一个程序，读入两个正整数n和m（1<=n<m<1000），输出[n,m]范围内所有的完数。

提示：可以写一个函数来判断某个数是否是完数。

输入格式:

两个正整数，以空格分隔。

输出格式：

其间所有的完数，以空格分隔，最后一个数字后面没有空格。如果没有，则输出一个空行。

输入样例：

1 10

输出样例：

6

代码

import java.util.Scanner;

public class AllNumber {
	
	public static boolean judegefactor(int i){  //判断是否为素数
		boolean judegefactor = true;
		for(int k =2; k<i;k++) {
			if(i%k==0) {
				judegefactor = false;
				break;
			}
		}
		return judegefactor;
	}
	
	public static int wanshu(int a,int b) { //定义一个函数
		int sum = 0;
		for(int num=a;num <= b;num++) {
			if(!judegefactor(num)) {
				for(int i = 1;i<num;i++) {
					if(num%i==0)
					{
						sum +=i;
					}
				}
				if(sum==num) {//验证是否为完数
					System.out.println(num);
				}
				sum=0;
			}
		}
		return sum;
	}

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner in = new Scanner(System.in);
		int n = in.nextInt();
		int m = in.nextInt();
		if(n>=1&&n<m&&m<1000) {
			wanshu(n,m);
		}else {

		System.out.print("您输入的数据有误");
	}
	}
}

运行结果