理解记忆法
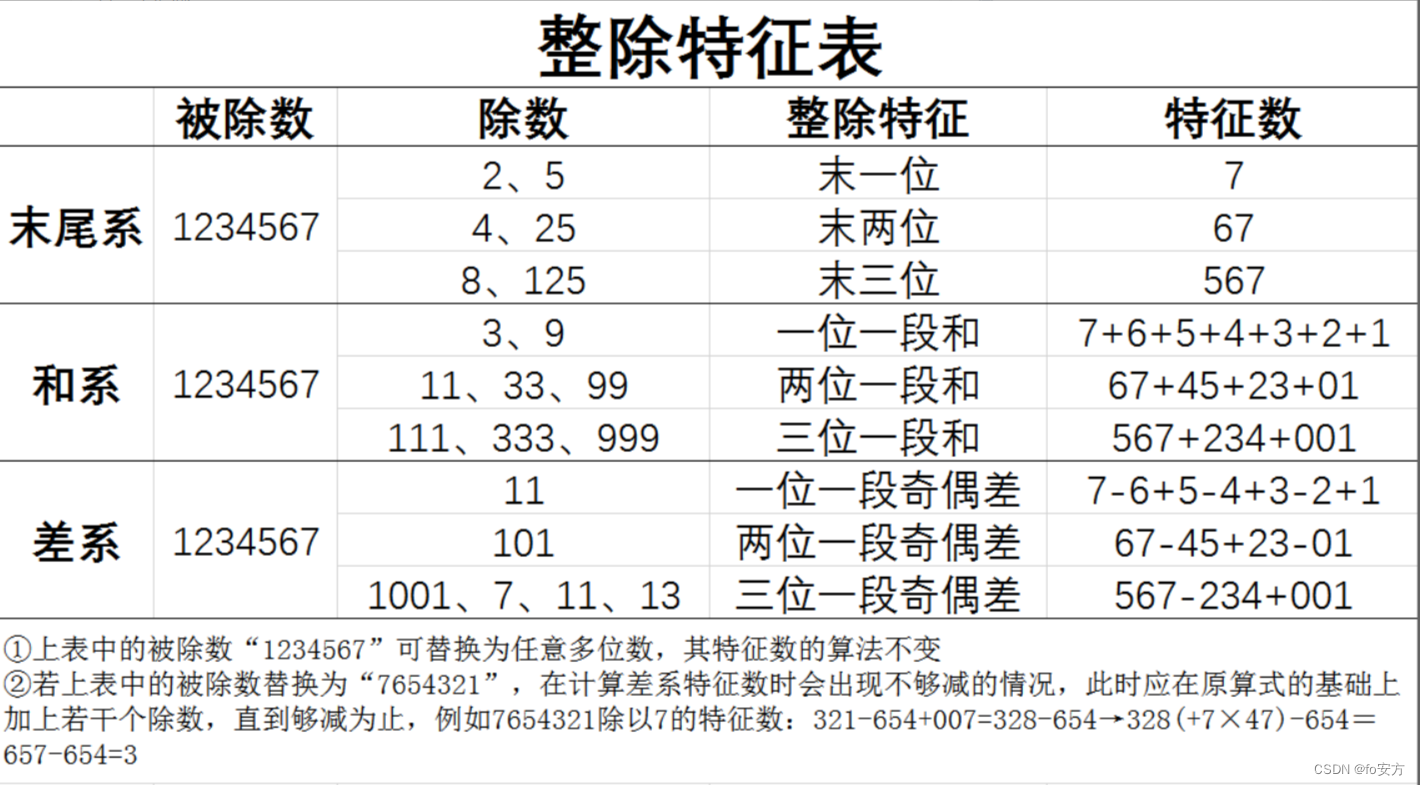
对于数的整除特征大家都比较熟悉:比如4看后两位(因为100是4的倍数),8看后三位(因为1000是8的倍数),5末尾是0或5,3与9看各位数字和等等,今天重点研究一下3,9,7,11,13的整除特征(重点是三位截断法的原理)。继续用字母来代替数来推导公式,弄清原理又锻炼代数与证明问题能力。
①3,9的整除特征(各位数字和)
设三位数abc(a,b,c等代表0-9的数字,以下同样),用位值原理拆开
100a+10b+c
=(99+1)a+(9+1)b+c
=99a+9b+a+b+c
由于前两项都是9的倍数,不影响除以9的余数,所以a+b+c就是这个数除以9的余数。如果除以9余0,那么这个数就是9的倍数。
②11的整除特征(奇位数字和与偶位数字和的差)
把一个数由右边向左边数,如果奇位上数字和与偶位上数字和的差,是11的倍数(包括0),那么这个数就是11的倍数。
首先10的奇数次方减去1就是11的倍数,例如10000-1=9999,100-1=99
其次10的偶数次方加上1也是11的倍数,例如1000+1=1001,10+1=11
设五位数abcde,用位值原理拆开
10000a+1000b+100c+10d+e=9999a+1001b+99c+11d+a-b+c-d+e
前4项都是11的倍数,不影响除以11的余数。所以如果a-b+c-d+e是11的倍数,那么这个数就是11的倍数。
(由于是减法,可能出现负数,可以加上11的倍数变成非负的再判断;或者用偶数位和减去奇数位和,用它们的差判断就可以)
③三位截断法(后三位截断作差)的原理(7,11,13)
这种方法利用1001=7×11×13
设六位数abcdef,用位值原理拆开
1000abc+def=1001abc-abc+def
第一项是1001的倍数,可以不考虑它。
只看def-abc即可(如果为负数,可以用abc-def来判断,即def与abc的差)
例如def与abc的差是13的倍数,那么abcdef就是13的倍数。
如果位数比较大可以多截几次
例:判断593654321是否是7,11,13的倍数。
593654-321=593333;593-333=260;
因为260不是7,11的倍数,
所以593654321不是7,11的倍数。
因为260是13的倍数,
所以593654321就是13的倍数。








![[unity]保存文件的路径设置](https://img-blog.csdnimg.cn/02fc94df4ae44579b0051ad8b21e4bca.png)