详解OpenCV的椭圆曲线点坐标近似计算函数ellipse2Poly()

函数ellipse2Poly()可用于近似计算椭圆曲线的像素坐标。
而前面介绍过的函数ellipse()则是直接在图像中绘制椭圆，详情见 https://www.hhai.cc/thread-174-1-1.html

函数ellipse2Poly()的C++原型如下：

void cv::ellipse2Poly(Point center,
                      Size axes,
                      int angle,
                      int arcStart,
                      int arcEnd,
                      int delta,
                      std::vector< Point > & pts)

函数ellipse2Poly()的Python原型如下：

pts=cv.ellipse2Poly(center, axes, angle, arcStart, arcEnd, delta)

参数意义如下：
center—椭圆的中心坐标。
axes—椭圆的长半轴和短半轴的长度。
angle—椭圆旋转的角度，单位为度。
arcStart–椭圆孤起始的角度，单位为度。
arcEnd—椭圆弧终止的角度，单位为度。
delta—点与点之间的角度分辨率，其实就是对椭圆曲线的近似度。
pts—存储椭圆曲线像素坐标的数组。

上面的各参数除了参数delta不太好理解，其它都很好理解。

对于参数delta的意义，通过两个例子，大家就清楚了。

我们把函数ellipse2Poly()近似得到的曲线绘制出来，示例代码及运行结果如下：

# -*- coding: utf-8 -*-
# 出处：昊虹AI笔记网(hhai.cc)
# 用心记录计算机视觉和AI技术
# OpenCV的版本为4.4.0

import numpy as np
import cv2 as cv

if __name__ == '__main__':
    img = np.zeros((400, 400, 3), dtype='uint8')

    points = cv.ellipse2Poly((200, 200), (100, 70), 0, 0, 360, 3)  # 参数delta=3
    # points = cv.ellipse2Poly((200, 200), (100, 70), 0, 0, 360, 30)  # 参数delta=30

    for i in range(len(points) - 1):
        img = cv.line(img, (points[i][0], points[i][1]), (points[i + 1][0], points[i + 1][1]),
                      (255, 0, 0), 2, cv.LINE_4, 0)

    cv.imshow('Image', img)
    cv.waitKey(0)
    cv.destroyAllWindows()
    

当delta=3时的运行结果如下：

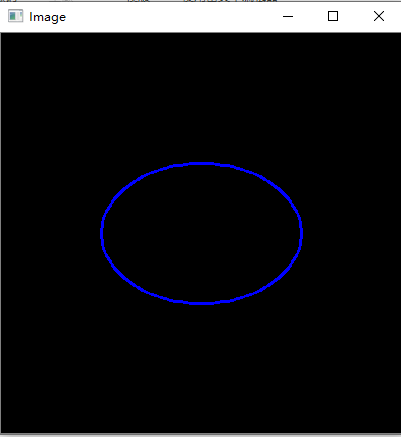
当delta=30时的运行结果如下：

通过上面的运行结果和示例代码，大家就知道函数函数ellipse2Poly()中参数delta的意义了，也知道函数ellipse2Poly()的使用方法了。

接下来，再附一个函数ellipse2Poly()的C++示例代码：

//出处：昊虹AI笔记网(hhai.cc)
//用心记录计算机视觉和AI技术

//OpenCV版本 OpenCV3.0

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace std;
using namespace cv;

int main()
{
	Mat A1 = Mat::zeros(400, 400, CV_8UC3);

	std::vector< Point > points;

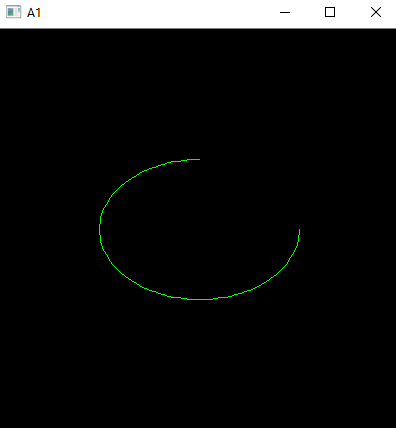
	ellipse2Poly(Point(200, 200), Size(100, 70), 0, 0, 270, 3, points);

	int i = 0;

	for (int i = 0; i < points.size() - 1; i++)
	{
		line(A1, points[i], points[i+1], Scalar(0, 255, 0));
	}


	imshow("A1", A1);
	cv::waitKey(0);

	return(0);
}

运行结果如下：