1.情景概述

        假设最一般的情况，我们的机械臂有六个自由度，那么从初始状态想要变化到目标的状态，一般情况下我们至少需要进行六次的变换，而这六次变换的矩阵参数隐含在整体的变换矩阵中。

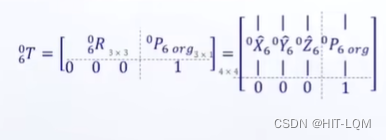
         根据之前的知识，左上角的3*3代表了三个单位向量的转置，这九个数6个限制条件：模长为一、两两垂直，决定了有三个自由度。右上角的3*1代表了平移变换，共三个自由度。而我们6次的变换都有12个三角函数关系式，对应着6个未知数和6个限制条件，我们的目标就是为了求解这六个未知数。

2.求解概念

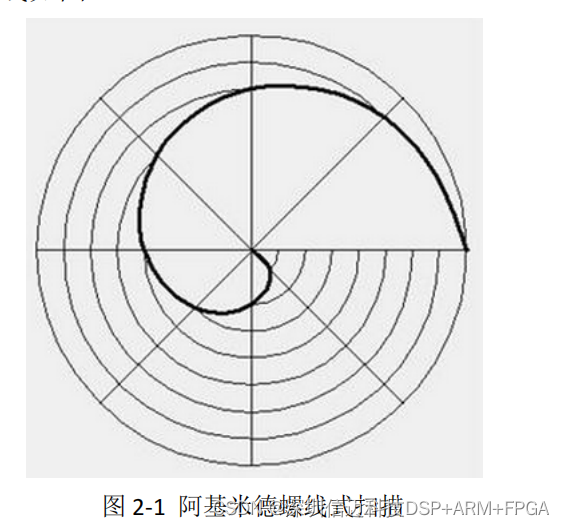
2.1Reachable workspace

机械臂可以用一种以上的姿态到达的位置，左图的同心圆以及右图的圆（不包括边界）。

2.2Dexterous workspace

机械臂可以用任何的姿态到达的位置，右图的中心点。

2.3Subspace

机械臂在定义头尾的变换矩阵T所能到达的变动范围

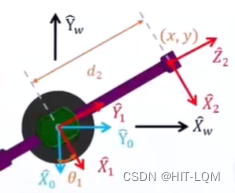
 比如这个2自由度的机械臂，引入（x,y）坐标，那么他的T是固定的：

可以看到，如果（x,y）一定，那么实际上左边的角度也都是确定的；而且，所能到达的位置也是有限的，因为旋转矩阵的九个数字已经有五个数字是确定的，只有四个数字可以发生变化。

2.4多重解

很多时候，到达一个点有多种驱动的实现方式，举一个例子，PUMA（6 rotational joints）

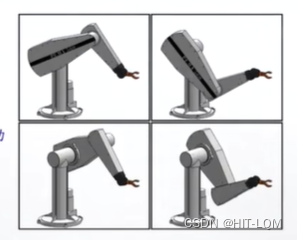
 针对特定的工作点，前三轴会对应四种姿态，而每种姿态，具有两种的手腕转动姿态，因此共有八组解。不难发现这些角度有如下的关系：

 但是由于机械结构的限制，未必每组解都会成为可行解。

选择解的方式要考虑以下几点：

1.相对于目前状态最快实现

2.相对于目前状态最节能

3.可以躲避障碍物

3.求解方法 

3.1解析法

解析法分为代数法或几何法。目前来讲设计的大多数手臂都存在解析解，而且为了便于求解，通常将后三个轴交于一点。

3.2数值法

3.3求解过程

下面我们来看一个例子，分析其求解过程。

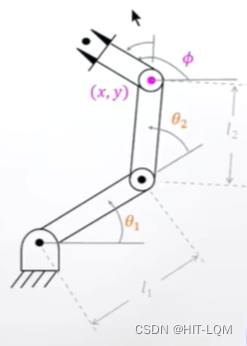
 我们已知的条件是（x,y,φ），目标是要求解（θ1，θ2，θ3），即：

已知：    ，来求解

 

几何法：空间几何拆解成平面几何

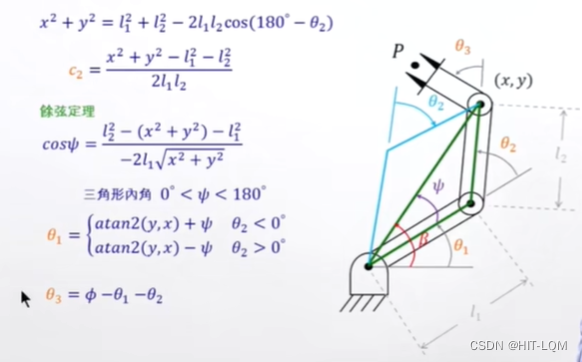
 量化计算结果如下所示：

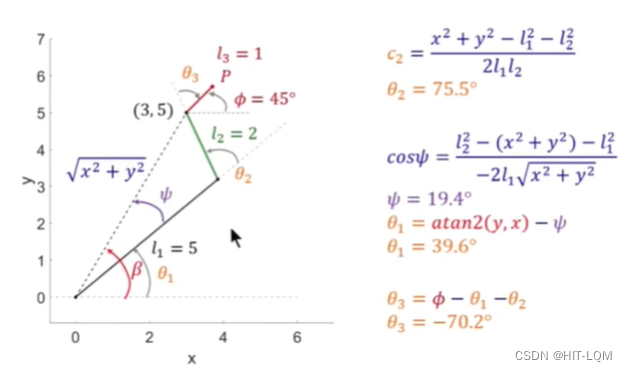
 代数法：建立方程式

 首先根据两个矩阵建立方程式，通过观察首先求解θ2，然后通过大小判断是否有解，有几组解：

 其次将θ2带入方程式：

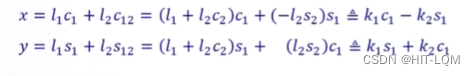
 再进行变数变换：

 随后求解θ1：

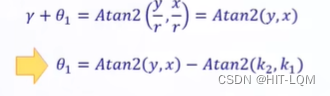
当我们的θ2选择不同的解，θ1也会跟着产生变化。

最后求解θ3：

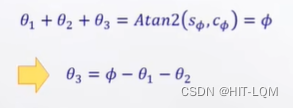
 三角函数方程式的求解