1Lagrange Duality Formulate the Lagrange dual problem of the following
linear programming prob-lem min cT rs.t.Ax 二b where a ∈R is variable,c
∈ R",A ∈Rk×n, b ∈ Rk.

解:设拉格朗日函数为 L ( x , λ ) = c T x + λ T ( A x − b ) \mathcal{L}(x,\lambda)=c^Tx+\lambda^T(Ax-b) L(x,λ)=cTx+λT(Ax−b),
对应的对偶函数为 G ( λ ) = i n f λ L ( x , λ ) \mathcal{G}(\lambda)=inf_{\lambda}\ \mathcal{L}(x,\lambda) G(λ)=infλ L(x,λ),
而LP问题与对偶问题强对偶,KTT 条件成立,满足 stationarity
∇ x c T x ∗ + λ ∗ T ( A x − b ) = 0 \nabla_{x}c^Tx^*+{\lambda^*}^T(Ax-b)=0 ∇xcTx∗+λ∗T(Ax−b)=0
⟹ \Longrightarrow ⟹ c T + λ ∗ T A = 0 c^T+{\lambda^*}^TA=0 cT+λ∗TA=0
以及 A x ∗ − b = 0 Ax^*-b=0 Ax∗−b=0,因此该点处拉格朗日函数可以表达为
L ( x ∗ , λ ∗ ) = ( − λ T A ) ( A − 1 b ) + λ T ( A x ∗ − b ) \mathcal{L}(x^*,\lambda^*)=(-\lambda^TA)(A^{-1}b)+\lambda^T(Ax^*-b) L(x∗,λ∗)=(−λTA)(A−1b)+λT(Ax∗−b)
L ( x ∗ , λ ∗ ) = − λ T b \mathcal{L}(x^*,\lambda^*)=-\lambda^T b L(x∗,λ∗)=−λTb
根据 Dual feasibility 得 λ i ≥ 0 \lambda_i\geq 0 λi≥0
LP问题的对偶问题标准形式为
m
a
x
λ
−
λ
T
b
s
.
t
.
λ
≥
0
,
c
T
+
λ
T
A
=
0
max_{\lambda}\ -\lambda^T b \\ s.t. \lambda\geq 0,c^T+{\lambda}^TA=0
maxλ −λTbs.t.λ≥0,cT+λTA=0
这里补充一种做法:
将拉格朗日对偶函数变换为
G
(
λ
)
=
i
n
f
L
(
x
,
λ
)
=
i
n
f
(
c
T
+
λ
T
A
)
x
−
λ
T
b
\mathcal{G}(\lambda)=inf\mathcal{L}(x,\lambda)=inf(c^T+\lambda^TA)x-\lambda^Tb
G(λ)=infL(x,λ)=inf(cT+λTA)x−λTb,
当
c
T
+
λ
T
A
=
0
c^T+\lambda^TA=0
cT+λTA=0 时,
G
(
λ
)
=
−
λ
T
b
\mathcal{G}(\lambda)=-\lambda^Tb
G(λ)=−λTb;
否则,
G
(
λ
)
=
∞
\mathcal{G}(\lambda)=\infty
G(λ)=∞,不存在极值。
sVM
2.1Convex Functions Prove f(w) = w" . (where w ∈ R") is a convex function.2.2Soft-Margin for Separable Data Consider training a
soft-margin SVM with C set to some positive constant.Suppose the
training data is linearly separable. Since increasing the 6; can
onlyincrease the objective of the primal problem (which we are trying
to minimize),at the optimal solution to the primal problem,all the
training examples willhave functional margin at least 1 and all the i
will be equal to zero. True orfalse? Explain! Given a linearly
separable dataset, is it necessarily better to usea a hard margin SVM
over a soft-margin SVM?
2.3In-bound Support Vectors in Soft-Margin sVMs Examples ar() with a > 0 are called support vectors (SVs). For soft-marginsVM we distinguish
between in-bound SVs,for which 0 <Qi<C, and boundsVs for which a; = C.
Show that in-bound SVs lie exactly on the margin.Argue that bound SVs
can lie both on or in the margin,and that they will“usually” lie in
the margin. Hint: use the KKT conditions.

2.1证: ω T ω \omega^T\omega ωTω是凸函数
⟺ \iff ⟺ ∣ ∣ λ x + ( 1 − λ ) y ∣ ∣ 2 ≤ λ ∣ ∣ x ∣ ∣ 2 + ( 1 − λ ) ∣ ∣ y ∣ ∣ ||\lambda x+(1-\lambda)y||^2\leq \lambda||x||^2+(1-\lambda)||y|| ∣∣λx+(1−λ)y∣∣2≤λ∣∣x∣∣2+(1−λ)∣∣y∣∣
⟺ \iff ⟺ λ ∣ ∣ x ∣ ∣ 2 + ( 1 − λ ) ∣ ∣ y ∣ ∣ − ( λ x + ( 1 − λ ) y ) T ( λ x + ( 1 − λ ) y ) ≥ 0 \lambda||x||^2+(1-\lambda)||y||-(\lambda x+(1-\lambda)y)^T(\lambda x+(1-\lambda)y)\geq 0 λ∣∣x∣∣2+(1−λ)∣∣y∣∣−(λx+(1−λ)y)T(λx+(1−λ)y)≥0
⟺ \iff ⟺ λ ∣ ∣ x ∣ ∣ 2 + ( 1 − λ ) ∣ ∣ y ∣ ∣ − ( λ x T + ( 1 − λ ) y T ) ( λ x + ( 1 − λ ) y ) ≥ 0 \lambda||x||^2+(1-\lambda)||y||-(\lambda x^T+(1-\lambda)y^T)(\lambda x+(1-\lambda)y)\geq 0 λ∣∣x∣∣2+(1−λ)∣∣y∣∣−(λxT+(1−λ)yT)(λx+(1−λ)y)≥0
⟺ \iff ⟺ λ ∣ ∣ x ∣ ∣ 2 + ( 1 − λ ) ∣ ∣ y ∣ ∣ − ( λ 2 x T x + λ ( 1 − λ ) ( y T x + y T x ) + ( 1 − λ ) 2 y T y ) λ ( 1 − λ ) ( y T x + y T x ) ≥ 0 \lambda||x||^2+(1-\lambda)||y||-(\lambda^2 x^Tx+\lambda(1-\lambda)(y^Tx+y^Tx)+(1-\lambda)^2y^Ty)\lambda(1-\lambda)(y^Tx+y^Tx)\geq 0 λ∣∣x∣∣2+(1−λ)∣∣y∣∣−(λ2xTx+λ(1−λ)(yTx+yTx)+(1−λ)2yTy)λ(1−λ)(yTx+yTx)≥0
⟺ \iff ⟺ ( λ − λ 2 ) x T x + ( λ − λ 2 ) y T y − λ ( 1 − λ ) ( y T x + y T x ) ≥ 0 (\lambda-\lambda^2)x^Tx+(\lambda-\lambda^2)y^Ty-\lambda(1-\lambda)(y^Tx+y^Tx)\geq 0 (λ−λ2)xTx+(λ−λ2)yTy−λ(1−λ)(yTx+yTx)≥0
⟺ \iff ⟺ ( λ − λ 2 ) x T x + ( λ − λ 2 ) y T y − λ ( 1 − λ ) ( y T x + y T x ) ≥ 0 (\lambda-\lambda^2)x^Tx+(\lambda-\lambda^2)y^Ty-\lambda(1-\lambda)(y^Tx+y^Tx)\geq 0 (λ−λ2)xTx+(λ−λ2)yTy−λ(1−λ)(yTx+yTx)≥0
而 λ ∈ [ 0 , 1 ] \lambda\in[0,1] λ∈[0,1],因此 λ ≥ λ 2 \lambda\geq \lambda^2 λ≥λ2,
⟺ \iff ⟺ x T x + y T y − ( y T x + y T x ) ≥ 0 x^Tx+y^Ty-(y^Tx+y^Tx)\geq 0 xTx+yTy−(yTx+yTx)≥0
⟺ \iff ⟺ ( x T − y T ) ( x − y ) ≥ 0 (x^T-y^T)(x-y)\geq 0 (xT−yT)(x−y)≥0
⟺ \iff ⟺ ∣ ∣ x − y ∣ ∣ 2 ≥ 0 ||x-y||^2\geq 0 ∣∣x−y∣∣2≥0
而 ∣ ∣ x − y ∣ ∣ 2 ≥ 0 ||x-y||^2\geq 0 ∣∣x−y∣∣2≥0成立,故 ω T ω \omega^T\omega ωTω是凸函数,证毕。
2.2不一定,软间隔SVM模型表达为
m
i
n
ω
,
b
,
ξ
1
2
∣
∣
ω
∣
∣
2
+
C
∑
i
=
1
m
ξ
i
s
.
t
.
y
(
i
)
(
ω
T
x
(
i
)
+
b
)
≥
1
−
ξ
i
ξ
i
≥
0
,
∀
i
=
1
,
2
,
.
.
.
,
m
min_{\omega,b,\xi}\frac{1}{2}||\omega||^2+C\sum^m_{i=1}\xi_i \\ s.t. y^{(i)}(\omega^Tx^{(i)}+b)\geq1-\xi_i \\ \xi_i\geq0,\forall i=1,2,...,m
minω,b,ξ21∣∣ω∣∣2+Ci=1∑mξis.t.y(i)(ωTx(i)+b)≥1−ξiξi≥0,∀i=1,2,...,m
考虑一维情形如下
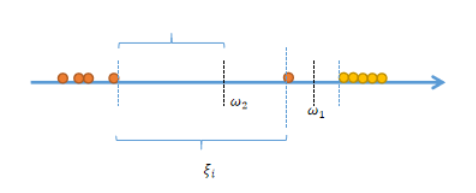
令 ∀ ξ i = 0 \forall\xi_i=0 ∀ξi=0,即退化为硬间隔SVM,求得决策边界为 ω 1 \omega_1 ω1;
令 ξ j = 0 , j ≠ i \xi_j=0,j\neq i ξj=0,j=i,求得决策边界为 ω 2 \omega_2 ω2;
目标函数设为 f f f, f ( ω 1 ) = 1 2 ω 1 2 f(\omega_1)=\frac{1}{2}\omega_1^2 f(ω1)=21ω12, f ( ω 2 ) = 1 2 ω 2 2 + C ξ i f(\omega_2)=\frac{1}{2}\omega_2^2+C\xi_i f(ω2)=21ω22+Cξi,
当 1 2 ω 1 2 > 1 2 ω 2 2 + C ξ i \frac{1}{2}\omega_1^2>\frac{1}{2}\omega_2^2+C\xi_i 21ω12>21ω22+Cξi时, ξ i \xi_i ξi可以不为0, ω 2 \omega_2 ω2优于 ω 1 \omega_1 ω1,因而最优解一定不是 ω 1 \omega_1 ω1.
软间隔SVM可以避免过拟合,正如上面的例子,右侧橙色点可能是噪声,用硬间隔SVM会拟合噪声;
相反,前者通过松弛变量,泛化模型,提高鲁棒性,因此某些情况下有必要使用软间隔SVM。
2.3①当 0 < α i ∗ < C 0<\alpha^*_i<C 0<αi∗<C时,
根据KTT条件 α i ∗ + r i ∗ = C \alpha^*_i+r^*_i=C αi∗+ri∗=C得 0 < r i ∗ < C 0<r^*_i<C 0<ri∗<C,
又因为 r i ∗ ξ i ∗ = 0 r^*_i\xi^*_i=0 ri∗ξi∗=0,所以 ξ i ∗ = 0 \xi^*_i=0 ξi∗=0,
因为 α i ∗ ( y ( i ) ( ω ∗ T x ( i ) + b ∗ ) + ξ i ∗ − 1 ) = 0 \alpha^*_i(y^{(i)}({\omega^*}^Tx^{(i)}+b^*)+\xi^*_i-1)=0 αi∗(y(i)(ω∗Tx(i)+b∗)+ξi∗−1)=0,
所以 y ( i ) ( ω ∗ T x ( i ) + b ∗ ) + ξ i ∗ − 1 = 0 y^{(i)}({\omega^*}^Tx^{(i)}+b^*)+\xi^*_i-1=0 y(i)(ω∗Tx(i)+b∗)+ξi∗−1=0,
所以 y ( i ) ( ω ∗ T x ( i ) + b ∗ ) = 1 y^{(i)}({\omega^*}^Tx^{(i)}+b^*)=1 y(i)(ω∗Tx(i)+b∗)=1,
即 in-bound SVs 在支撑平面上。
②当 α i ∗ = C \alpha^*_i=C αi∗=C时,类似的可以得到 y ( i ) ( ω ∗ T x ( i ) + b ∗ ) + ξ i ∗ − 1 = 0 y^{(i)}({\omega^*}^Tx^{(i)}+b^*)+\xi^*_i-1=0 y(i)(ω∗Tx(i)+b∗)+ξi∗−1=0,
而 ξ i ∗ ≥ 0 \xi^*_i\geq0 ξi∗≥0,因此 y ( i ) ( ω ∗ T x ( i ) + b ∗ ) ≤ 1 y^{(i)}({\omega^*}^Tx^{(i)}+b^*)\leq1 y(i)(ω∗Tx(i)+b∗)≤1,
即 bound SVs 在支撑平面上或者在间隔内。
而往往少数的点就能确定支撑平面(n 维空间 n 个点确定一个 boundary),因此大部分的点在间隔内。