文章目录
- 前言
- 一、字符串类型
- 字符串表示方法
- 二、数字类型
- 1. 整数
- 2.浮点数
- 3.复数
- 三、布尔类型
- 总结
前言
我们一般在电脑中存储的数据有多种数据类型。比如下图这张员工工资表:
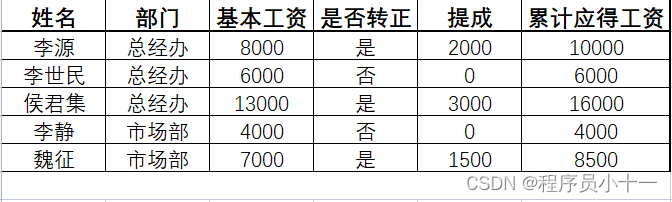
表中员工姓名可以用字符串类型存储(比如"李世民"、“侯君集”),工资可以用数字类型存储(比如6000、13000),是否转正可以用布尔类型存储(比如是、否)。这里所说的字符串类型、数字类型、布尔类型就是Python语言中所有的基本数据类型,也就是说在Python中我们是用这三种数据类型来表示和存储我们生活当中所有的数据,有没有四两拨千斤的意味呢?今天就跟大家详细说说Python中的这三大金刚。
一、字符串类型
字符串顾名思义就是连续的一串N多个字符,这个字符可以是中文、英文、符号等等所有能用电脑表示的一切字符。有小伙伴可能会问:如果是一个字符那叫什么呢?

这里告诉大家,在Python中,一个字符也要叫字符串。
字符串表示方法
在Python中,字符串的表示方法有如下三种:
- 单引号包裹起来的字符
- 双引号包裹起来的字符
- 三引号包裹起来的字符
这三种方法都是用来表示字符串的,并且含义一样。比如’abc’、“abc”、“”“abc”“”、‘’‘abc’''这些都表示的是字符串abc。那有大白肯定会说了:既然都能表示,而且含义一样,那搞一种就够了啊,搞三种不是脱裤子放屁-----多此一举嘛。

其实不然,三种表示方法一点也不鸡肋,其中单引号和双引号所包裹的字符序列必须在一行上,而三引号内的字符序列可以分布在连续的多行上。比如,我们要打印一首古诗,如果使用单引号或者双引号,最终所有的诗句都是显示在一行,并没有按照我们代码里面的格式进行显示:
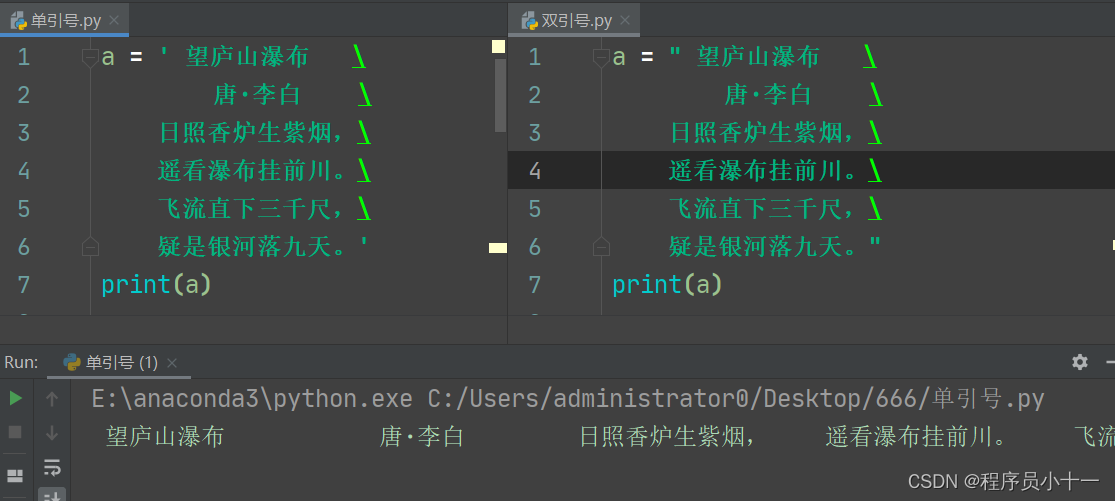
如果是三引号呢,我们看看:
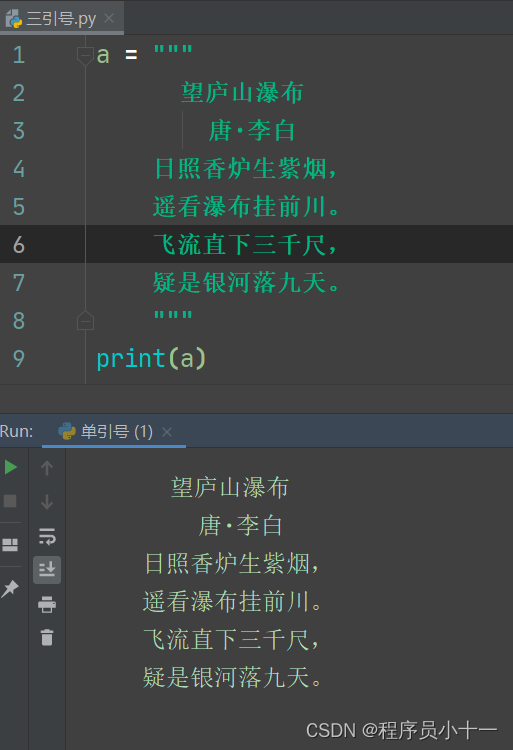
其次,单引号和双引号两种表示方法也不多余,比如很多时候我们需要字符串里面嵌套字符串就很方便,如下图:
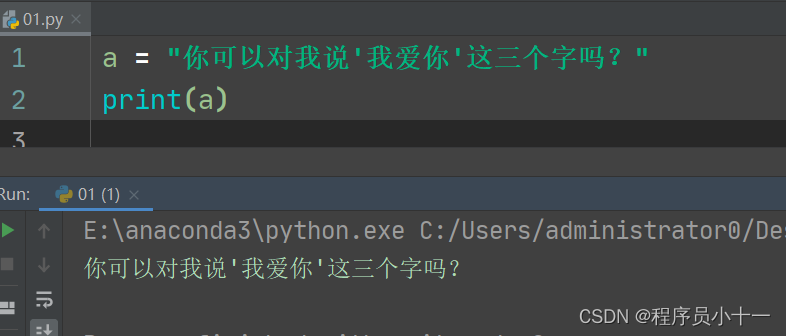
但是如果只有单引号一种或者双引号一种表示方法,这种嵌套情境下就会报错:
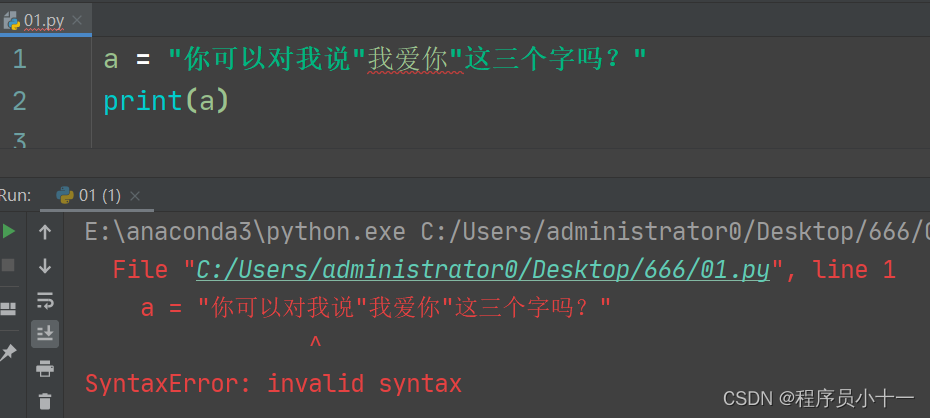
注意:三引号除了表示多行字符串之外,还可以用于多行注释(注释这块有不懂的小伙伴可以看我之前的博客)
二、数字类型
在生活中,我们经常使用数字进行各种记录,比如学生考试成绩、运动员比赛得分、产品销售数据等信息。在Python语言中,提供了数字类型用于保存这些数字,数字类型主要包括整数、浮点数和复数。
1. 整数
在Python中,整数有正整数、负整数和0。整数类型包括十进制整数、八进制整数、十六进制整数和二进制整数。看到这么多进制,很多小伙伴可能就蒙了:除了十进制,其他我咋都没听过。

莫慌,我先给大家说一下,其实除了十进制,其他进制在以后开发上基本很难用到。所以今天我只讲十进制,如果小伙伴想详细了解有关其他进制方面相关的知识,可以在评论区留言,我会接下来专门写一篇针对进制的博客。
十进制整数:十进制整数的表现形式大家都很熟悉,例如下面的数字都是有效的十进制整数。
0
23353457878
7978797898797897987979787979797979797979897979999789
-2022
注意:不能以数字0作为十进制数的开头(如果是单独的0除外),不然会报错如下图:
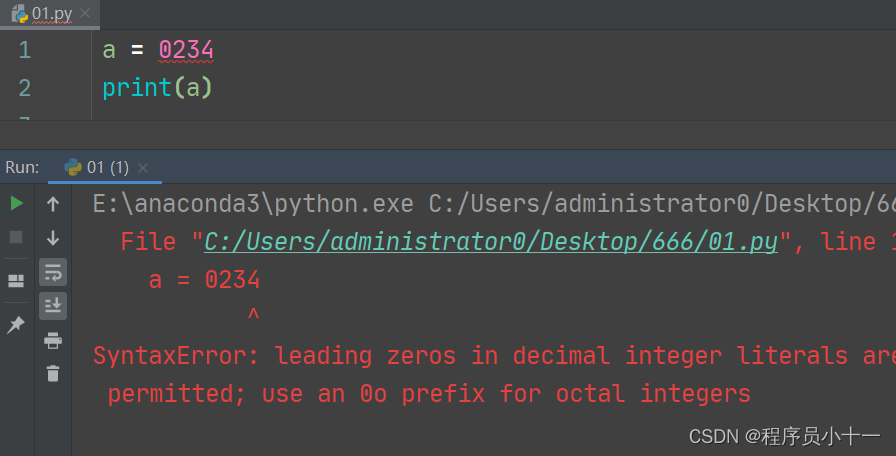
2.浮点数
浮点数其实就是我们常见的小数,例如:3.14、0.9、-1.88等等,这里就不多说了。
3.复数
复数这里作为了解,开发用不上。Python中复数与数学中的复数形式完全一致,都是由实部和虚部组成,并且使用小写字母j或者大写字母J表示虚部。当表示一个复数时,可以将其实部和虚部相加,例如一个复数,实部为5,虚部为8j,则这个复数为5+8j。
三、布尔类型
布尔类型主要用来表示真值或假值。在Python中,保留字True和False被解释为布尔值,True表示为真,False表示为假。此外,Python中的布尔值可以转化为数值:True表示1,False表示0,并且进行算术运算,如下图所示:

我们可以看到代码中分别打印输出了True+10的结果为11,False+10的结果为10。
总结
上述给大家讲的Python三种基本数据类型,在后续的开发中运用最多的还是字符串类型,其次是数字和布尔类型。再说一点,数字类型里面我们以后基本用的都是十进制整数和浮点数(小数),二、八、十六进制以及复数几乎很少用到。