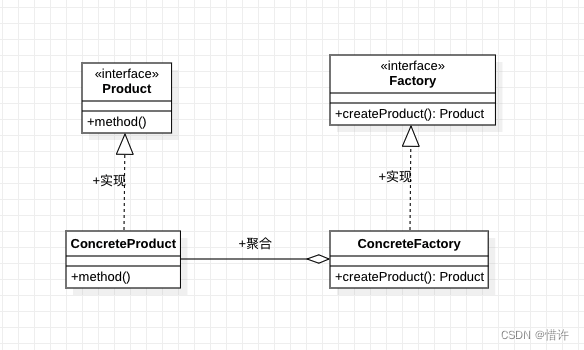
设计

根据二叉树的中序遍历的迭代解法，稍改代码，就是本题的解法。

初始化 : 传入了根结点，根据迭代思路，将结点的左链依次入栈。

$next$ : 栈顶结点就是所求。根据迭代思路，当前结点要变成栈顶结点的右儿子。由于 $next$ 只想取个值，我们要帮他找到下一个中序结点，将当前结点的左链依次入栈。

$hasnext$ : 结点按中序遍历入栈，看栈内有没有元素，就知道有没有取完结点了。

class BSTIterator {
public:
    stack<TreeNode *> stk;
    BSTIterator(TreeNode* root) {
        while(root){
            stk.push(root);
            root = root->left;
        }
    }
    
    int next(){
        auto t = stk.top();
        stk.pop();
        int ans = t -> val;
        t = t->right;
        while(t){
            stk.push(t);
            t = t->left;
        }
        return ans;
    }

    bool hasNext() {
        return stk.size();
    }
};

1. 时间复杂度 : $O(1)$ ， $h$ 是二叉树的最大深度， 对于每个查询， $next$ 最坏时间复杂度 $O(h)$ ，对应走 $h$ 的深度才找到下一个结点。如果查询整个二叉树，每个结点最多入栈一次， $next$ 均摊时间复杂度 $O(1)$ 。
2. 空间复杂度 : $O(h)$ ， 最坏空间复杂度 $O(h)$ 。

AC

致语

• 理解思路很重要！
• 欢迎读者在评论区留言，墨染看到就会回复的。