LeetCode 76. 最小覆盖子串（困难）

【题目描述】

给你一个字符串 s、一个字符串 t。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 ""。

注意：

• 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
• 如果 s 中存在这样的子串，我们保证它是唯一的答案。

【示例1】

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

【示例2】

输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。

【示例3】

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

【提示】

$1\le s.length,t.length\le 10^5$
s 和 t 由英文字母组成

【分析】

---

本题是滑动窗口的一个经典的应用，我们枚举 s 中的每个右端点 $i$，对于每个 $i$ 都找出最近的一个左端点 $j$，使得 s[j, i] 中包含 t 中的所有字符。

能用滑动窗口（双指针）的题目一定要具有单调性，即当 $i$ 往右移动的过程中 $j$ 一定不会往左移动。假设 s[j, i] 中已经包含 t 中的所有字符，那么当 $i$ 向右移动变为 $i^{\prime }$ 后 s[j, i'] 一定也包含 t 中的所有字符，因此 $j$ 不可能往左移动变成 s[j', i']。

还有一个问题是如何快速判断当前区间中是否包含 t 中的所有字符，我们可以用哈希表分别统计 t 中每个字符出现的次数（t_cnt）以及滑动窗口内每个字符出现的次数（s_cnt），然后使用一个变量 cnt 统计 t 中有多少字符被滑动窗口包含了，如果 cnt 等于 t 的长度则说明全部字符以及被包含了，那么如何精准统计 cnt 呢？分情况讨论即可：

• 若当前字符 c 在滑动窗口中出现的次数已经大于 t 中该字符的数量则不累计 cnt；
• 若当前字符 c 在滑动窗口中出现的次数小于等于 t 中该字符的数量则将 cnt 加一。

如果字符 s[j] 出现的次数大于 t 中该字符的数量则可以将 $j$ 向右移动。

---

【代码】

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> s_cnt, t_cnt;
        int cnt = 0;
        string res;
        for (auto &c: t) t_cnt[c]++;
        for (int i = 0, j = 0; i < s.size(); i++)
        {
            s_cnt[s[i]]++;
            if (s_cnt[s[i]] <= t_cnt[s[i]]) cnt++;
            while (s_cnt[s[j]] > t_cnt[s[j]]) s_cnt[s[j]]--, j++;
            if (cnt == t.size() && (res.empty() || i - j + 1 < res.size()))
                res = s.substr(j, i - j + 1);
        }
        return res;
    }
};

LeetCode 77. 组合（中等）

【题目描述】

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按任何顺序返回答案。

【示例1】

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

【示例2】

输入：n = 1, k = 1
输出：[[1]]

【提示】

$1\le n\le 20$
$1\le k\le n$

【分析】

---

DFS 搜索即可，需要注意判重，可以指定搜索顺序从小到大，即如果搜过 $i$ 后那么下一个数就从 $i+1$ 开始搜。

---

【代码】

class Solution {
public:
    vector<vector<int>> res;
    vector<int> v;

    vector<vector<int>> combine(int n, int k) {
        dfs(n, k, 1);
        return res;
    }

    void dfs(int n, int k, int now)
    {
        if (!k) { res.push_back(v); return; }
        for (int i = now; i <= n; i++)
        {
            v.push_back(i);
            dfs(n, k - 1, i + 1);
            v.pop_back();
        }
    }
};

LeetCode 78. 子集（中等）

【题目描述】

给你一个整数数组 nums，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。
解集不能包含重复的子集。你可以按任意顺序返回解集。

【示例1】

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

【示例2】

输入：nums = [0]
输出：[[],[0]]

【提示】

$1\le nums.length\le 10$
$-10\le nums[i]\le 10$
nums 中的所有元素互不相同

【分析】

---

这题如果用搜索来写其实和上一题一样，只需要枚举 $k$ 的大小，然后对于每个 $k$ 都 DFS 一遍即可，这种方式就不给出代码了。

或者也可以换一种方式搜索，对于每个数我们都可以选或不选一共有两种方案，在 DFS 的时候将这两种方案都考虑进去即可。

当我们想枚举每个数选或者不选这种子集时，可以使用一个二进制数来表示，例如要枚举三个数选或不选，就可以用一个三位的二进制数表示，当这个二进制数为 000 时表示三个数都不选，为 001 是表示只选第三个数，以此类推。

---

【代码】

【DFS 实现代码】

class Solution {
public:
    vector<vector<int>> res;
    vector<int> v;

    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u)
    {
        if (u == nums.size()) { res.push_back(v); return; }
        dfs(nums, u + 1);  // 不选nums[u]
        v.push_back(nums[u]);  // 选nums[u]
        dfs(nums, u + 1);
        v.pop_back();
    }
};

【迭代实现代码】

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        int n = nums.size();
        for (int i = 0; i < 1 << n; i++)
        {
            vector<int> v;
            for (int j = 0; j < n; j++)
                if (i >> j & 1) v.push_back(nums[j]);
            res.push_back(v);
        }
        return res;
    }
};

LeetCode 79. 单词搜索（中等）

【题目描述】

给定一个 m x n 二维字符网格 board 和一个字符串单词 word。如果 word 存在于网格中，返回 true；否则，返回 false。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

【示例1】

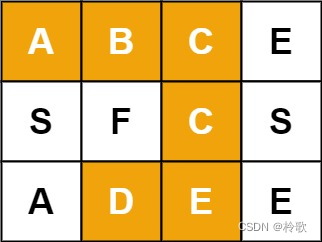
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

【示例2】

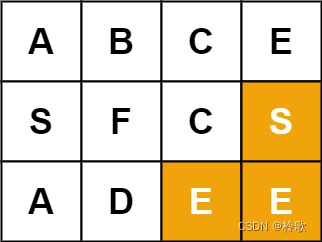
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

【示例3】

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

【提示】

$m==board.length$
$n==board[i].length$
$1\le m,n\le 6$
$1\le word.length\le 15$
board 和 word 仅由大小写英文字母组成

【分析】

---

---

【代码】