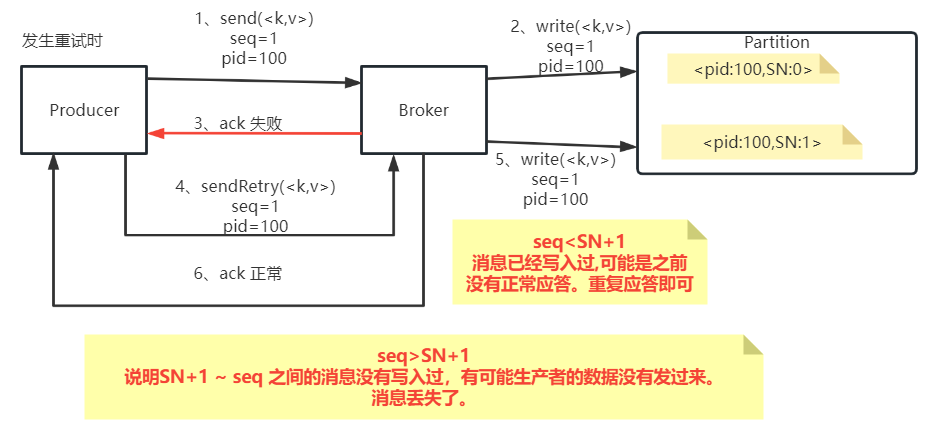
网格畸变是XY两个方向上的几何畸变，是不同视场实际像高与近轴像高的偏差。

垂轴放大率在整个视场范围内不能保持常数

当一个有畸变的光学系统对一个方形的网状物体成像时,若δy>0，则主光线的交点高度y比理想像高y低,视场越大，低得越多，形成一啤酒桶形状的图像,故又称正畸变为桶形畸变；

若δy<0,则y比理想像高y高，视场越大，高得越多，形成一种枕头形的图像，故负畸变又称枕形畸变。

​

一般对于畸变值小于4%的光学系统，我们是可以接受的。特殊应用的镜头除外。

 对畸变要求严格的光学系统往往采取对称或近似对称的结构形式。

畸变值的大小和光阑位置有关，如果在光阑两边的光学系统结构相互对称，且全系统的垂轴放大率为-1，则光学系统的垂轴像差为0.

网格畸变分析图可以解决非旋转对称和旋转对称系统的问题，但由于计算前提是预设像高与物空间视场角的正切成正比，在zemax中应用没有场曲/畸变分析图广泛；

这是因为当视场角大于等于90度时，该计算不能进行。

场曲/畸变分析图就没有这个限制

​

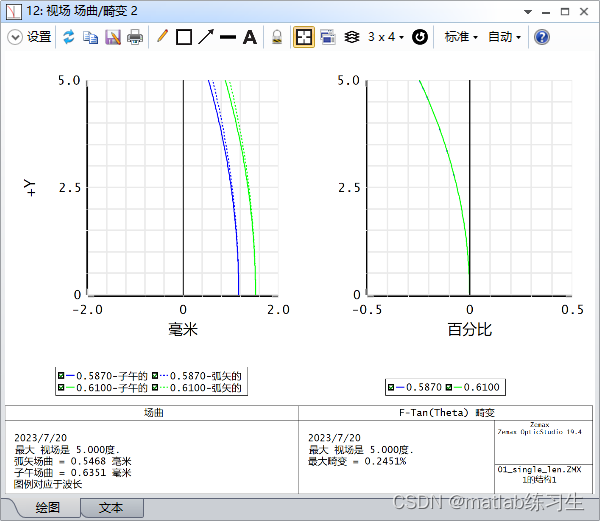
场曲/畸变分析图里面列举了四种畸变类型：F-tan畸变，F-theta畸变，校正的F-tan畸变，校正的F-theta畸变

​

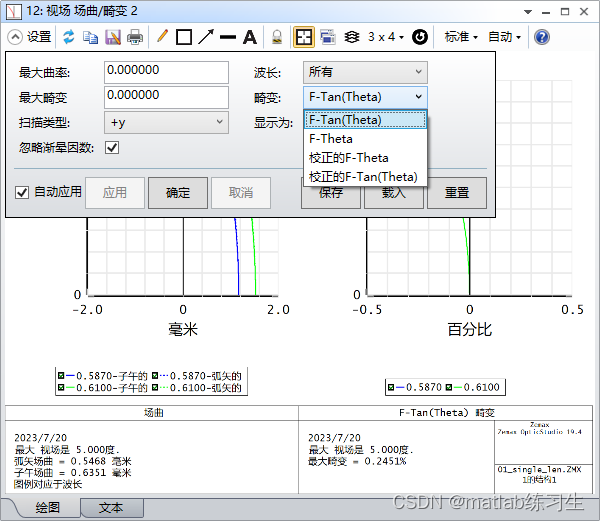
 计算相对畸变的公式为：

​

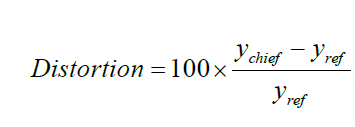
 对于上述的四种畸变类型，区别仅在于公式右边的y_ref不同。

• F-tan畸变：yref等于系统焦距乘以视场角的tan；
• F-theta畸变：yref等于系统焦距乘以视场角；
• 校正的F-tan畸变：yref等于拟合焦距乘以视场角的tan；
• 校正的F-theta畸变：yref等于拟合焦距乘以视场角

 

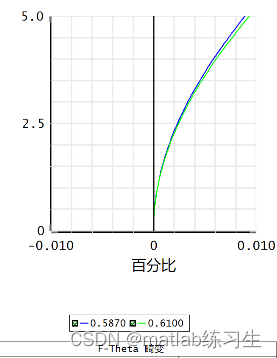
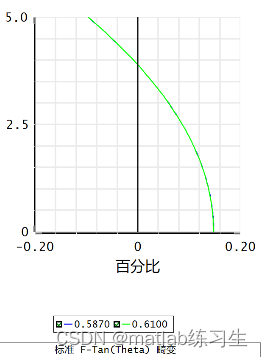
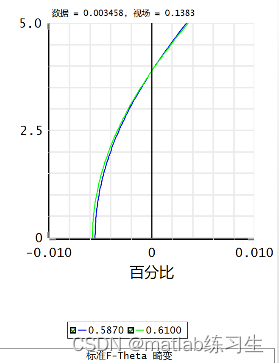
常规镜头用F-tan畸变，也就是系统的默认值，像高和视场角的正切成线性关系

扫描镜头用F-theta畸变

就像前面说的，“场曲/畸变”分析图只适合旋转对称系统

T子午场曲,S弧矢场曲

通过场曲/畸变分析图还能读出子午、弧矢场曲

在图中也有用颜色区分不同的场曲：

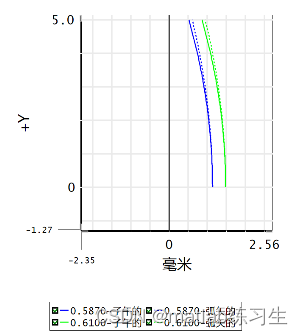
 横轴单位为centimeters厘米，纵轴最大视场为5度。 

场曲曲线显示作为视场坐标函数的当前的焦平面或像平面到近轴焦面的距离

子午场曲数据是沿着Z轴测量的从当前所确定的聚焦面到近轴焦面的距离，并且是在子午（YZ 面）上测量的。

弧矢场曲数据测量的是在与子午面垂直的平面上测量的距离，示意图中的基线是在光轴上，曲线顶部代表最大视场（角度或高度）