Scala第十章
news2026/2/14 16:43:14
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1057092.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
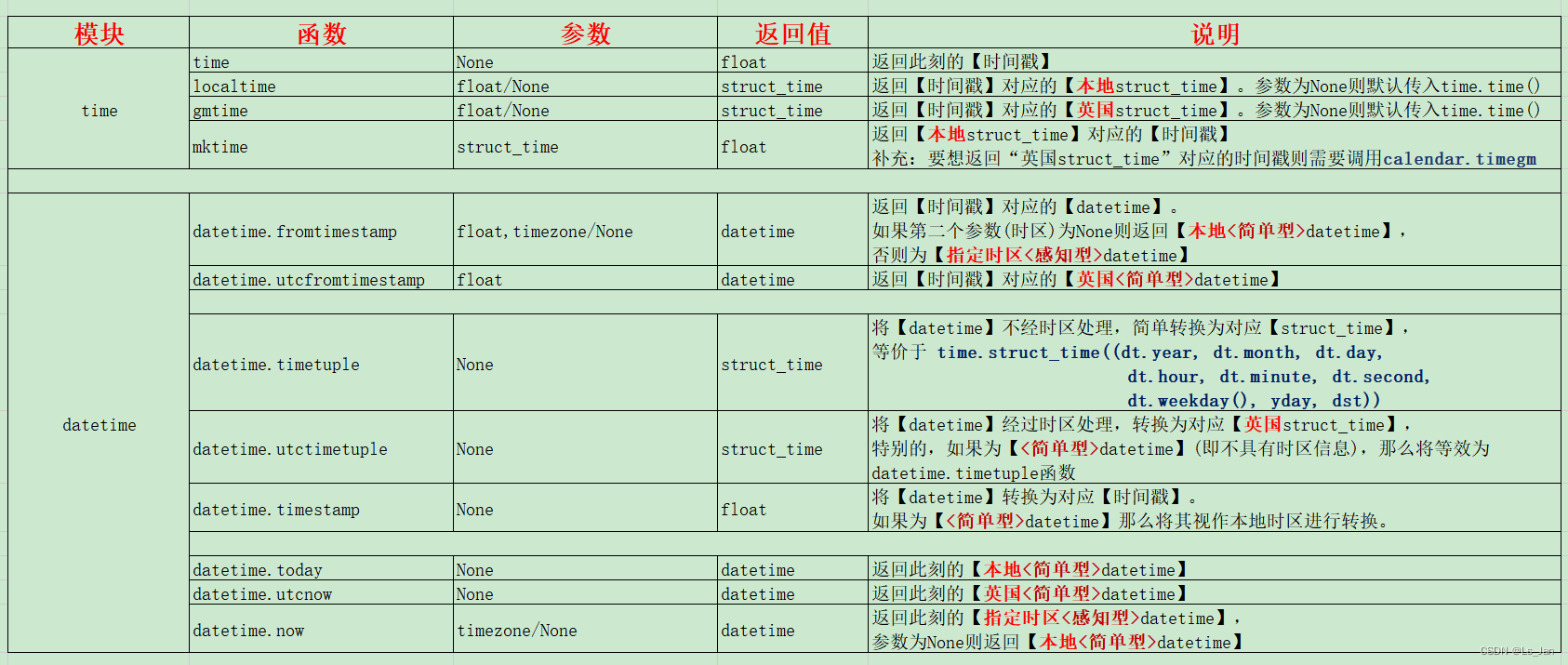
【Python】time模块和datetime模块的部分函数说明
时间戳与日期
在说到这俩模块之前,首先先明确几个概念:
时间戳是个很单纯的东西,没有“时区”一说,因为时间戳本质上是经过的时间。日常生活中接触到的“日期”、“某点某时某分”准确的说是时间点,都是有时区概念的…
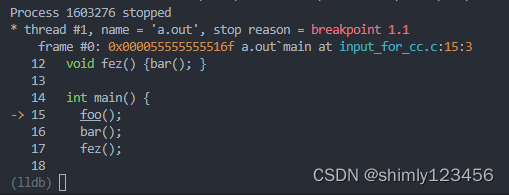
有时候,使用 clang -g test.c 编译出可执行文件后,发现 gdb a.out 进行调试无法读取符号信息,为什么?
经过测试,gdb 并不是和所有版本的 llvm/clang 都兼容的
当 gdb 版本为 9.2 时,能支持 9.0.1-12 版本的 clang,但无法支持 16.0.6 版本的 clang
可以尝试使用 LLVM 专用的调试器 lldb
我尝试使用了 16.0.6 版本的 lldb 调试 16.0.6 的 clan…
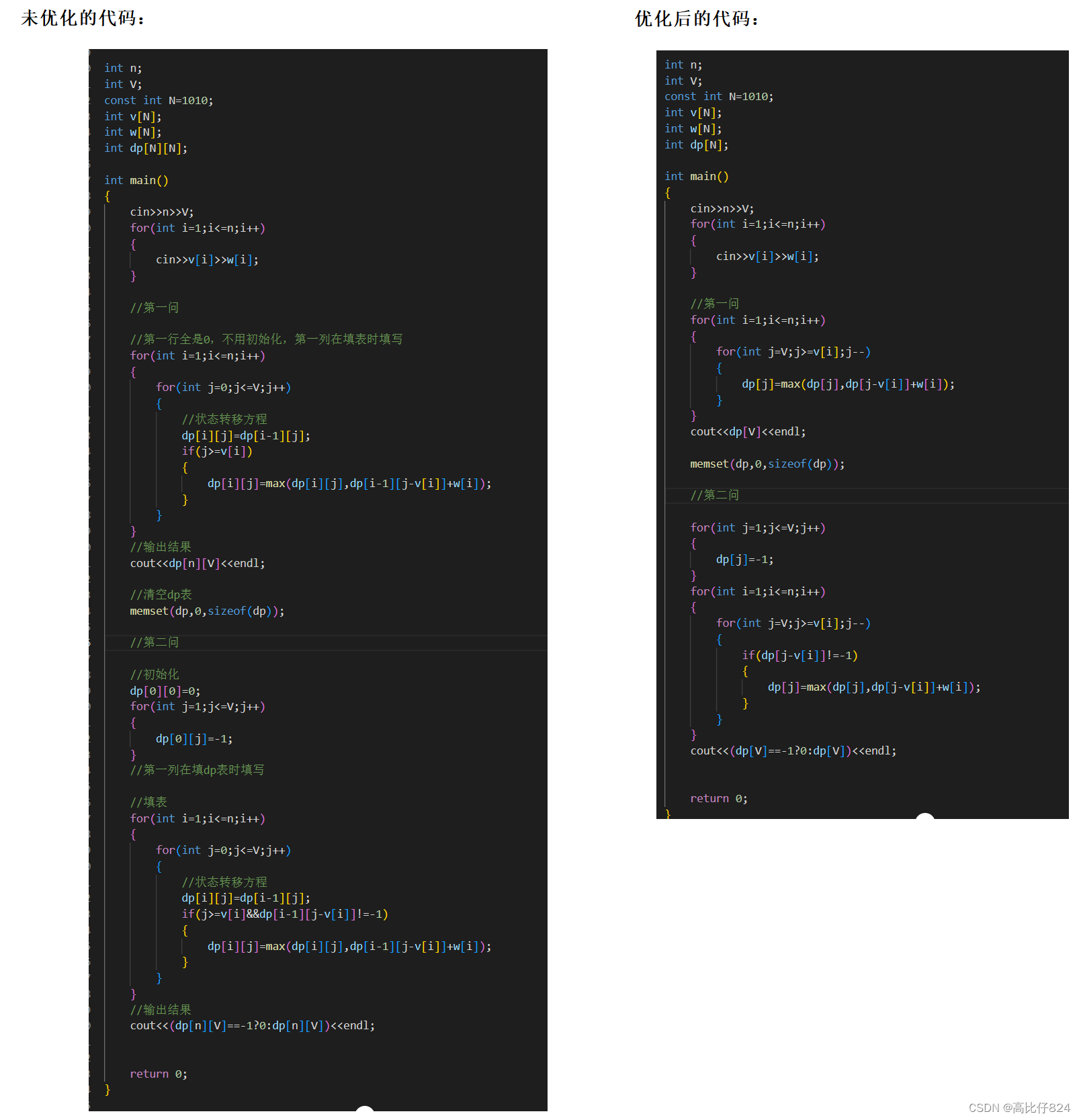
牛客题霸 -- DP41 【模板】01背包
解题步骤: 参考代码:
未优化的代码:
int n;
int V;
const int N1010;
int v[N];
int w[N];
int dp[N][N];int main()
{cin>>n>>V;for(int i1;i<n;i){cin>>v[i]>>w[i];}//第一问//第一行全是0,不用初…
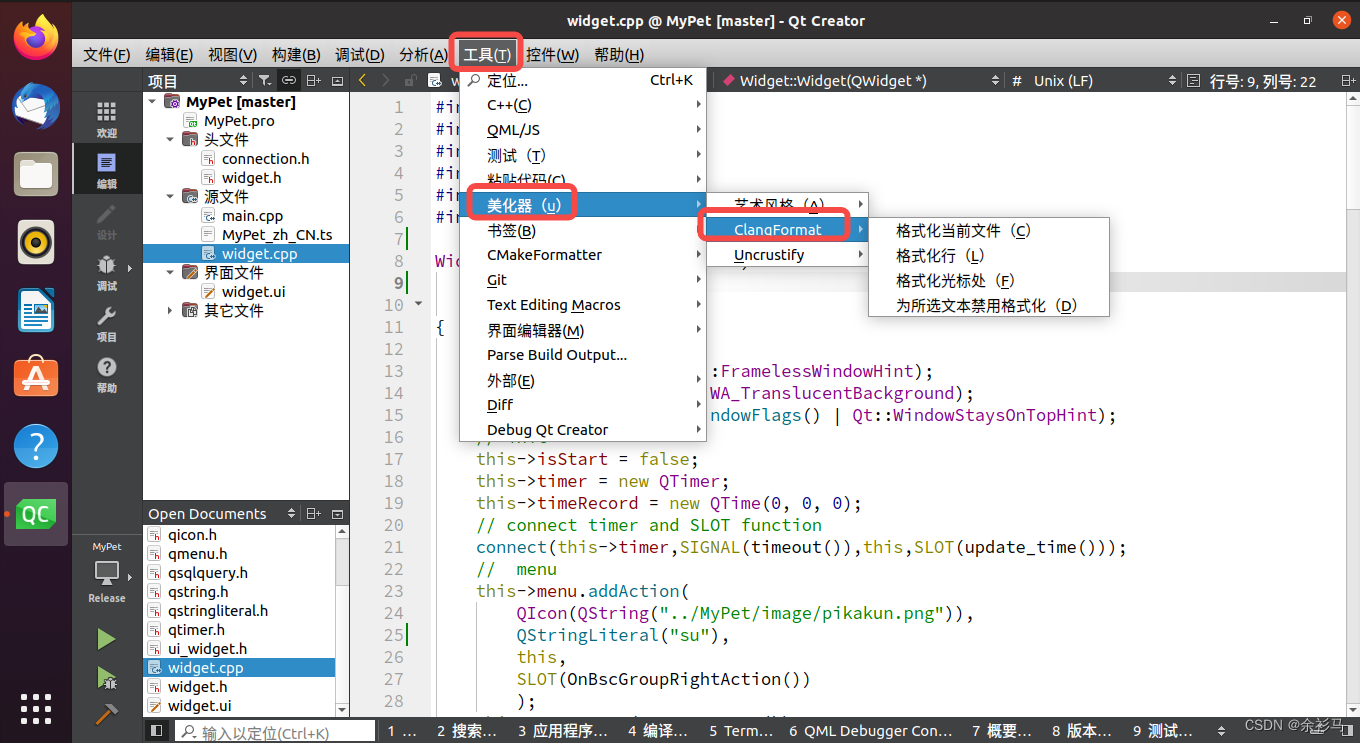
Ubuntu20 QT6.0 编译 ODBC 驱动
一、新建测试项目
新建一个控制台项目, // main.cpp #include <QCoreApplication>
#include <QSqlDatabase>
#include <QDebug>int main(int argc, char *argv[])
{QCoreApplication a(argc, argv);// 获取当前Qt支持的驱动列表QStringList driv…
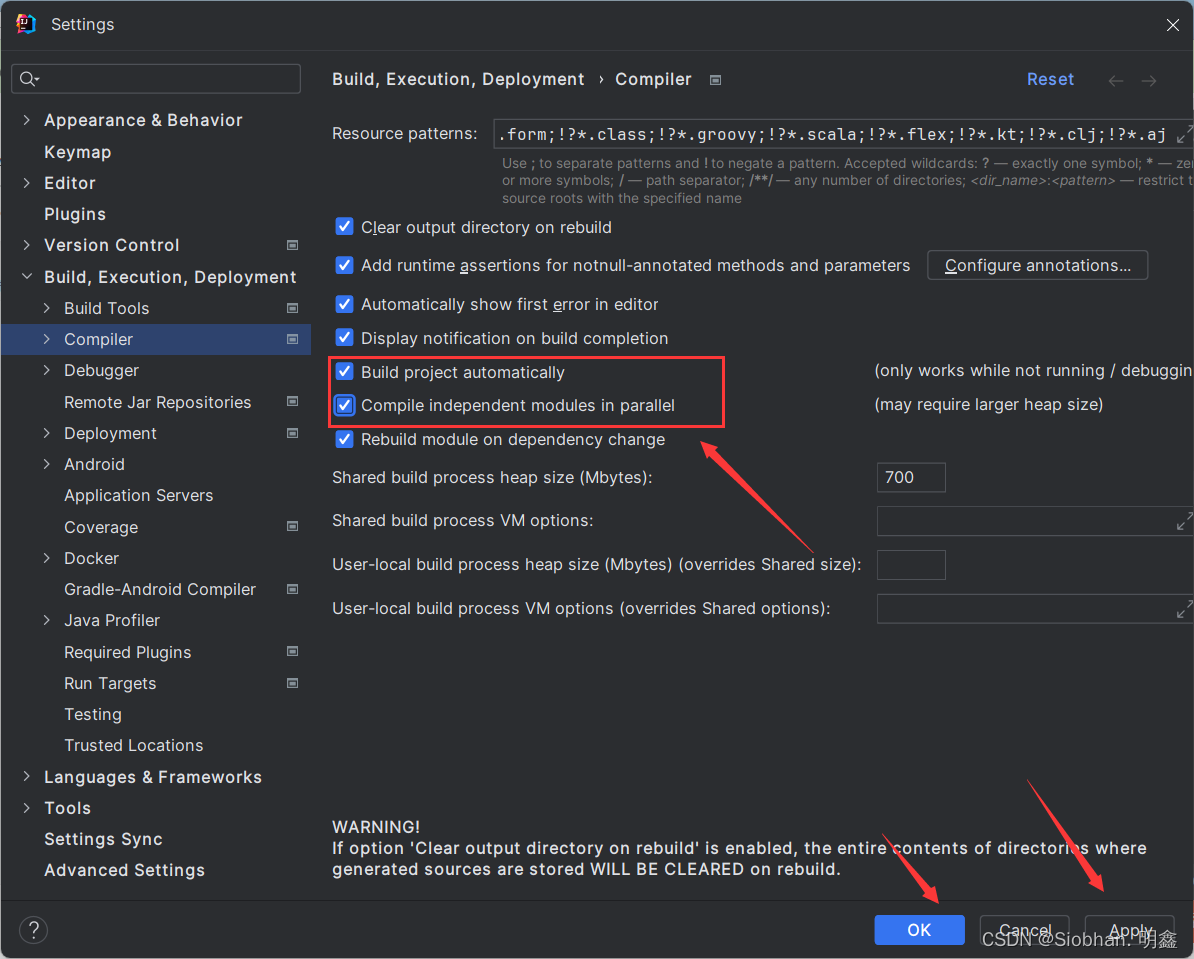
IDEA2023 常用配置(JDK/系统设置等常用配置)
目录
一、JDK及编译目录设置
1 项目的JDK设置
2 out目录和编译版本
二、相关详细设置
1 打开详细配置界面
1、显示工具栏
2、默认启动项目配置
3、取消自动更新
2 设置整体主题
1、选择主题 2、设置菜单和窗口字体和大小
3、设置IDEA背景图
3 设置编辑器主题样式…
八、混合整数线性规划问题
文章目录 1、混合整数线性规划问题2、分枝定界算法2.1、分枝策略 THE END 1、混合整数线性规划问题 \qquad 混合整数线性规划问题的一般表示形式如下所示:假设现有 n n n个变量, m m m个约束,令最大化(或者最小化) c 1 x 1 c 2 x 2 . . . …
数据结构与算法----递归
1、迷宫回溯问题 package com.yhb.code.datastructer.recursion¥5;public class MiGong {public static void main(String[] args) {// 先创建一个二维数组,模拟迷宫// 地图int[][] map new int[8][7];// 使用1 表示墙// 上下全部置为1for (int i 0; i…
VRRP配置案例(路由走向分析,端口切换)
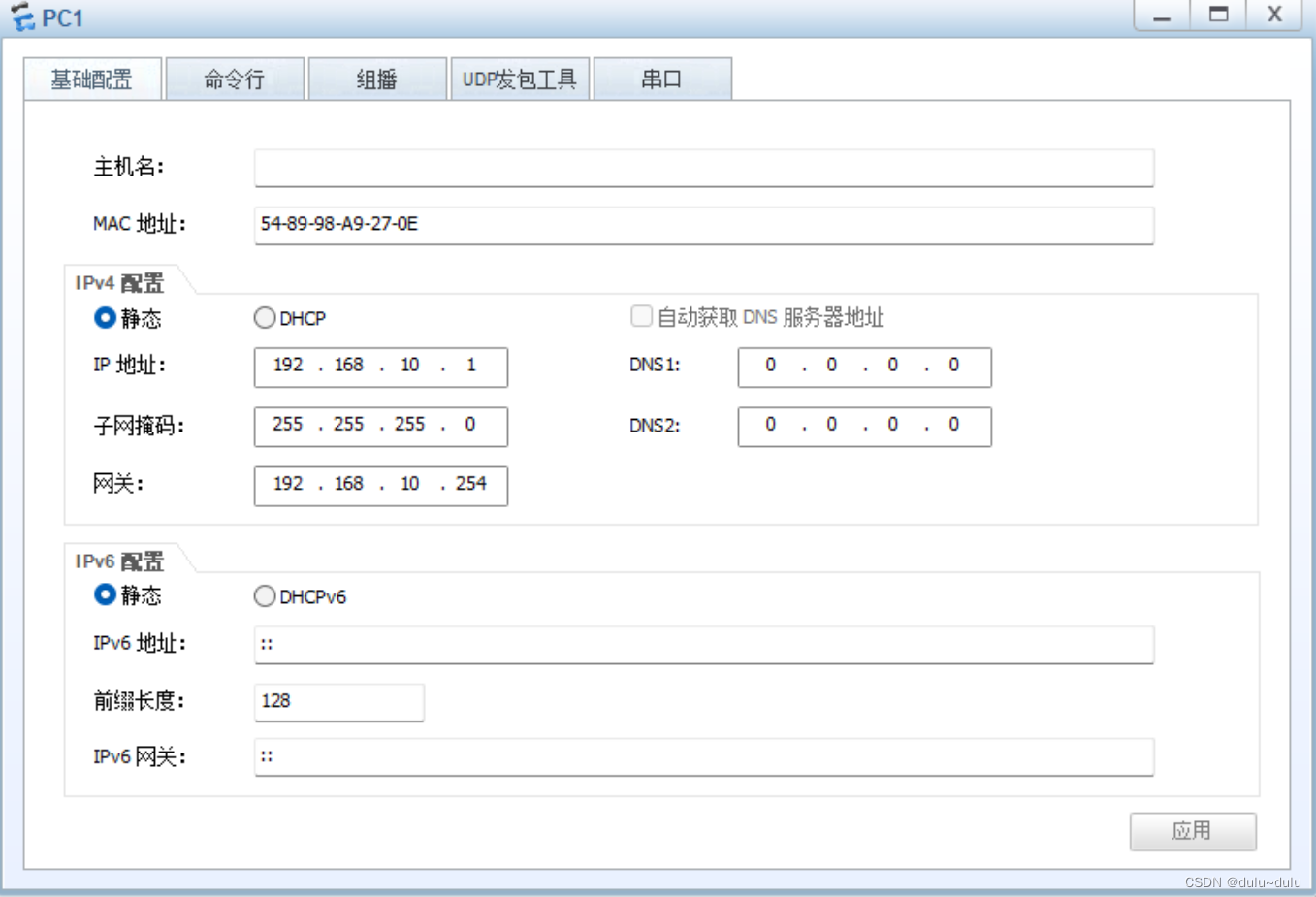
以下配置图为例 PC1的配置 acsw下行为access口,上行为trunk口, 将g0/0/3划分到vlan100中 <Huawei>sys
Enter system view, return user view with CtrlZ.
[Huawei]sysname acsw
[acsw]
Sep 11 2023 18:15:48-08:00 acsw DS/4/DATASYNC_CFGCHANGE:O…
嵌入式Linux应用开发-基础知识-第十九章驱动程序基石②
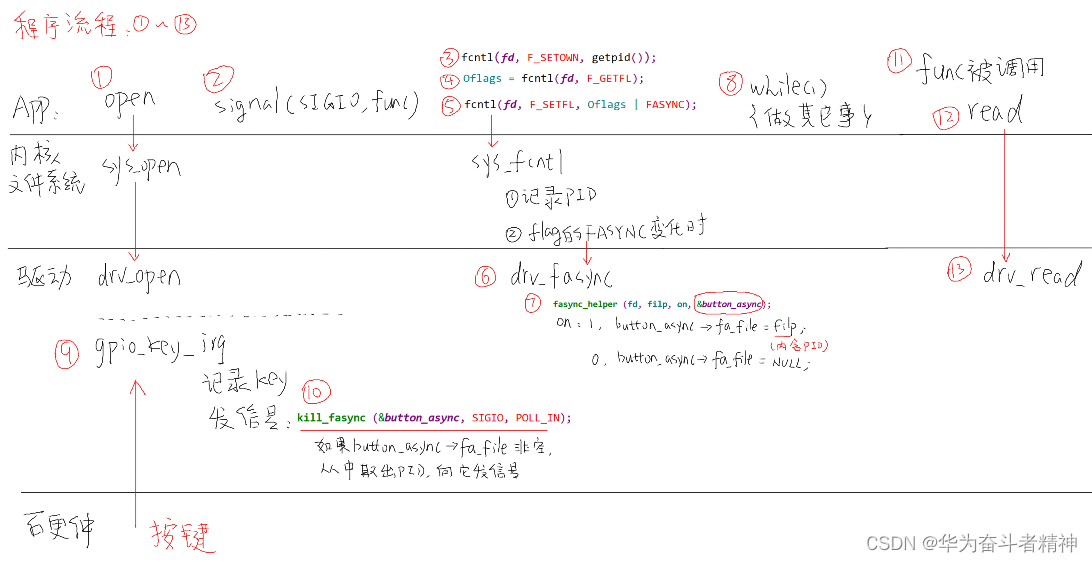
嵌入式Linux应用开发-基础知识-第十九章驱动程序基石② 第十九章 驱动程序基石②19.3 异步通知19.3.1 适用场景19.3.2 使用流程19.3.3 驱动编程19.3.4 应用编程19.3.5 现场编程19.3.6 上机编程19.3.7 异步通知机制内核代码详解 19.4 阻塞与非阻塞19.4.1 应用编程19.4.2 驱动编程…
Python无废话-办公自动化Excel修改数据
如何修改Excel 符合条件的数据?用Python 几行代码搞定。
需求:将销售明细表的产品名称为PG手机、HW手机、HW电脑的零售价格分别修改为4500、5500、7500,并保存Excel文件。如下图 Python 修改Excel 数据,常见步骤:
1&…
又添十万字-CS的陋室2023年文章合集来袭
趁着国庆中秋双节,整理了“22年文章合集”以来的所有新文章,在此给大家带来我的文章合集2023版。 文章合集收录: 文章合集2022以来的所有文章,包括“前沿重器”和“心法利器”。 前沿重器28-34共7篇,约2.6万字。心法利…
《C和指针》笔记30:函数声明数组参数、数组初始化方式和字符数组的初始化
文章目录 1. 函数声明数组参数2. 数组初始化方式2.1 静态初始化2.2 自动变量初始化 2.2 字符数组的初始化 1. 函数声明数组参数
下面两个函数原型是一样的:
int strlen( char *string );
int strlen( char string[] );可以使用任何一种声明,但哪个“更…
一文拿捏SpringMVC的调用流程
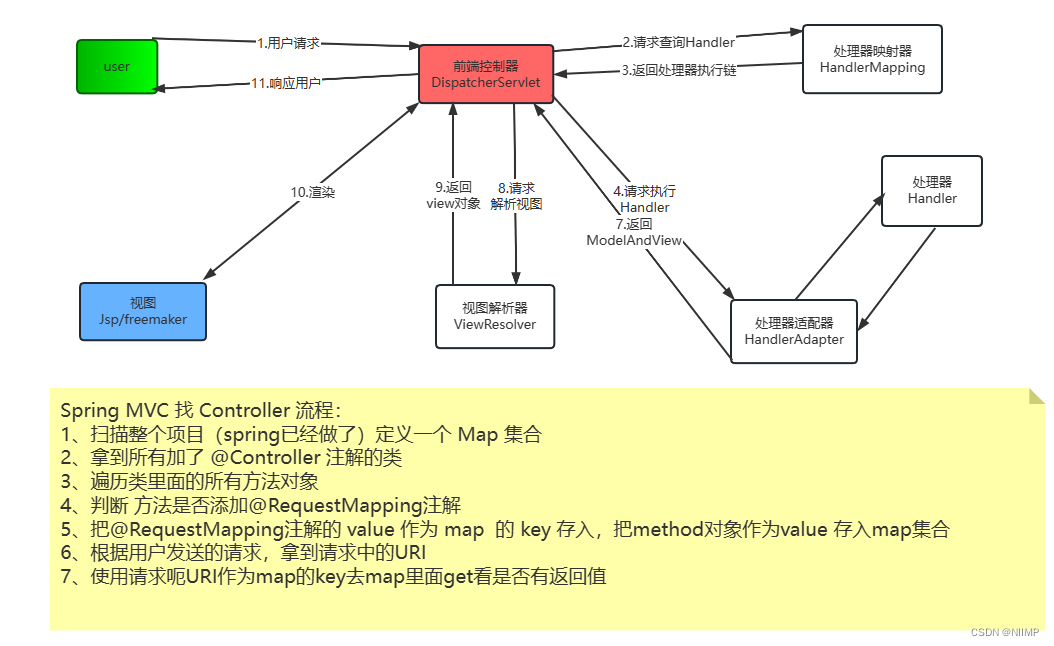
SpringMVC的调用流程 1.核心元素:
DispatcherServlet(前端控制器)HandlerMapping(处理器映射器)HandlerAdapter(处理器适配器) ---> Handler(处理器)ViewResolver(视图解析器 )---> view(视图) 2.调用流程
用户发送请求到前端控制器前端控制器接收用户请求…
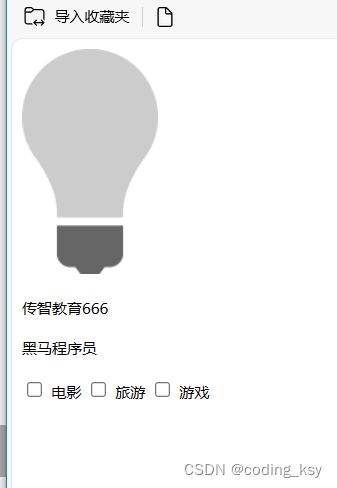
7.JavaScript-vue
1 JavaScript
html完成了架子,css做了美化,但是网页是死的,我们需要给他注入灵魂,所以接下来我们需要学习JavaScript,这门语言会让我们的页面能够和用户进行交互。
1.1 介绍
通过代码/js效果演示提供资料进行效果演…
<C++> STL_bitset使用和模拟实现
bitset的介绍
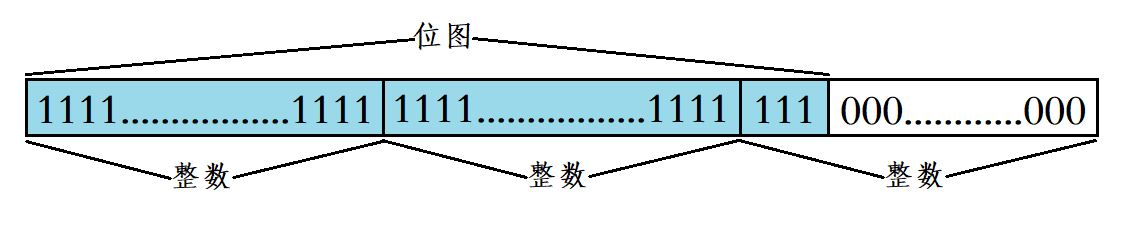
位图的引入
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
要判断一个数是否在某一堆数中,我们可能会想到如下方法:
将这一堆数进行排序࿰…
机器学习必修课 - 如何处理缺失数据
运行环境:Google Colab
处理缺失数据可简单分为两种方法:1. 删除具有缺失值的列 2. 填充
!git clone https://github.com/JeffereyWu/Housing-prices-data.git下载数据集
import pandas as pd
from sklearn.model_selection import train_test_split导…
EM@常用三角函数图象性质(中学部分)
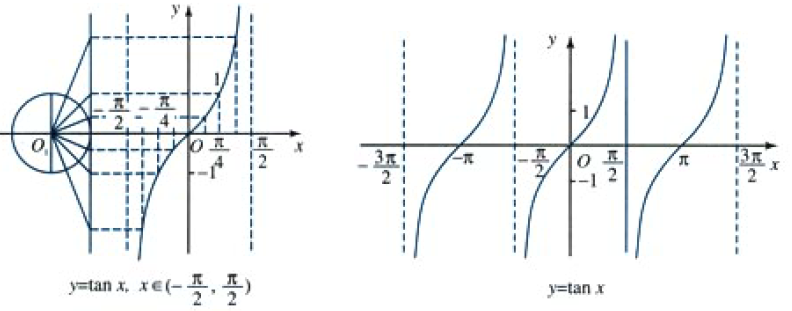
文章目录 abstract正弦函数正弦型函数转动相关概念旋转角速度转动周期转动频率初相小结 余弦函数的图象与性质性质 正切函数的图象和性质由已知三角函数值求角任意角范围内反三角函数(限定范围内)反正弦反余弦反正切 abstract
讨论 sin , cos , tan \sin,\cos,\tan s…
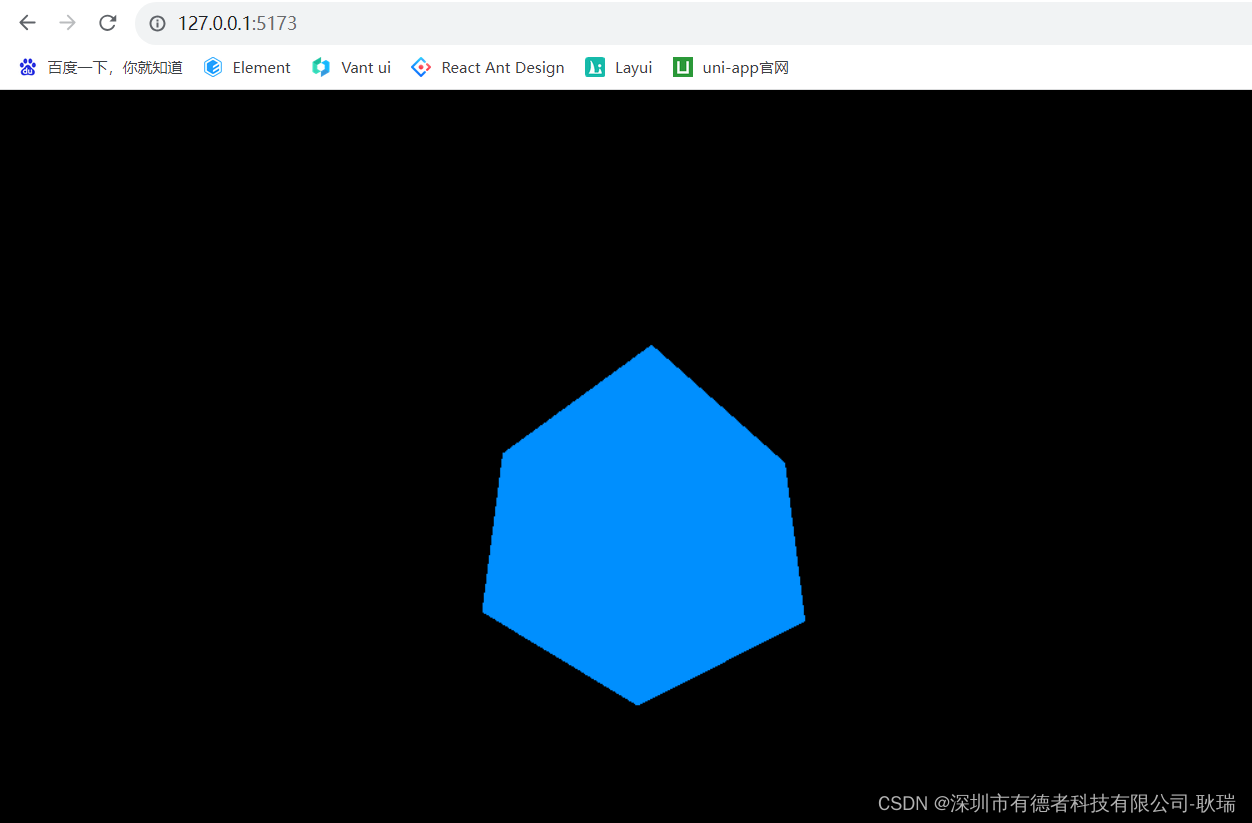
WEB 3D 技术,通过node环境创建一个three案例
好 文章 前端3D Three.js 在本地搭建一个官方网站 中我们 搭建了一个Three的官网
现在呢 我们就来创建第一个ThreeJs的资源 这里呢 我们还是选择一个脚手架的开发模式 因为现在基本所有的前端都在使用这样的开发方式 这里 我们创建一个文件夹目录 作为我们项目的存放目录 我们…
【MySQL教程】| (1-1) 2023MySQL-8.1.0 安装教程
文章目录 一、安装包下载二、安装配置1、解压安装包2、编写MySQL配置文件3、初始化MySQL数据库3、安装mysql服务并启动4、MySQL服务5、连接MySQL6、修改密码 三、配置环境变量四、防止mysql自启动拖慢开机时间 近日有粉丝问到mysql在win11的安装中遇到一些问题,应粉…