目录
一. 直接插入排序
基本思想
代码实现
时间和空间复杂度
稳定性
二. 希尔排序
基本思想
代码实现
时间和空间复杂度
稳定性
一. 直接插入排序
基本思想
把待排序的记录按其关键码值的大小依次插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
图解:
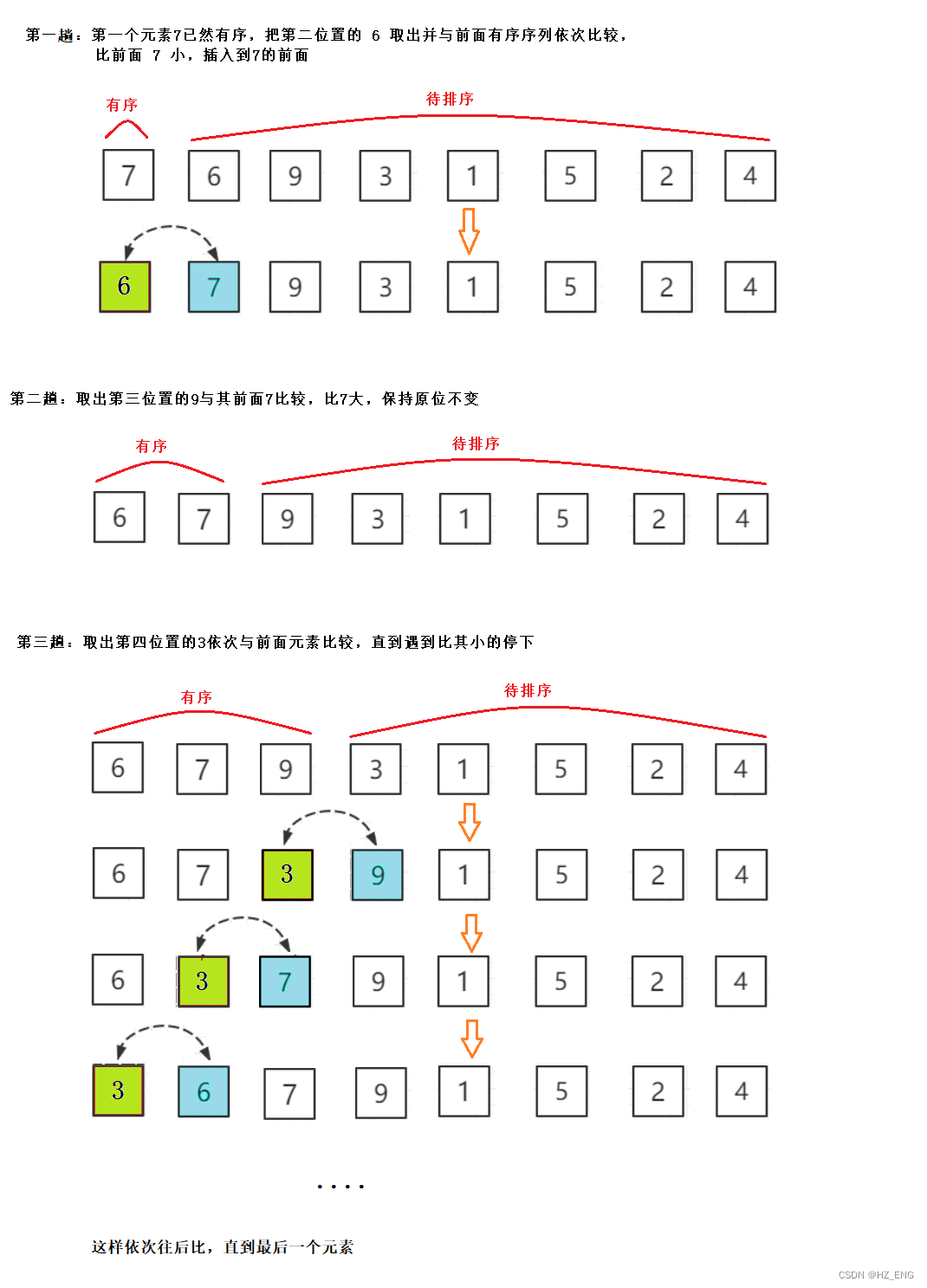
代码实现
//直接插入排序
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1 ; i++)
{
int j = i;
int tmp = a[j + 1]; //保存待排序元素
while (j >= 0)
{
if (tmp < a[j]) //将a[j+1]插入有序子表
a[j + 1] = a[j]; //记录后移位置
else
break;
j--;
}
a[j + 1] = tmp; //插入到正确位置
}
}
时间和空间复杂度
时间复杂度:o(n^2)
空间复杂度:o(1)
平均时间复杂度也是 O(n^2),空间复杂度为常数阶 O(1),具体时间复杂度和数组的有序性也是有关联的。
当待排序数组是有序时,是最优的情况,只需当前数跟前一个数比较一下就可以了,这时一共需要比较 N-1 次,时间复杂度为 O(N)。最坏的情况是待排序数组是逆序的,此时需要比较次数最多,最坏的情况是 O(n^2)。
说明:元素集合越接近有序,直接插入排序算法的时间效率越高
稳定性
一种排序实施前后,关键码相同的任意两个对象其前后次序没有发生变化,就说明这个排序是稳定的,否则是不稳定的。
直接插入排序:稳定排序
二. 希尔排序
希尔排序又称缩小增量排序,也是一种插入排序类的方法,此种方法是在直接插入排序的基础上改进的,在时间效率上有了很大的提高。
基本思想
以增量为步长划分子序列,即同一子序列中的逻辑上相邻元素,其下标步长等于增量。对每一个子序列进行直接插入排序。不断缩小增量,当增量为1时,所有数组元素都在一个子序列中排好序。
图示:
选择增量 gap = n / 2,缩小增量以 gap = gap / 2 的方式
注意:增量序列的最后一个增量值必须为1才行
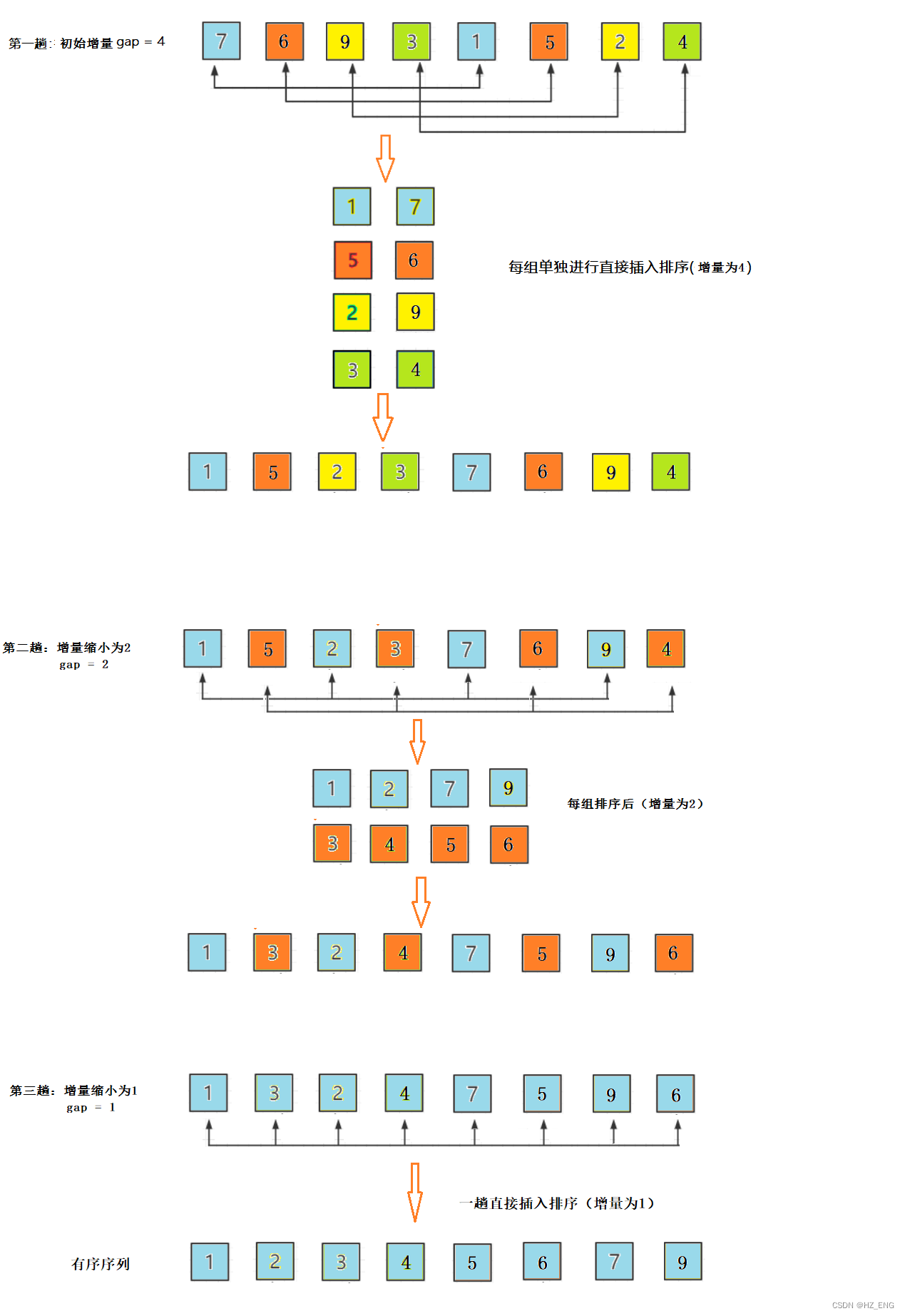
代码实现
代码一: 多组并排方式
图解
//希尔排序
void ShellSort(int* a, int n)
{
int gap = n; //增量初始值
while (gap > 1)
{
gap = gap / 2; //缩小增量
for (int i = 0; i < n - gap; i++) //对每一组进行直接插入排序
{
int j = i;
int tmp = a[j + gap];
while (j >= 0)
{
if (tmp < a[j])
{
a[j + gap] = a[j];
j -= gap;
}
else
break;
}
a[j + gap] = tmp;
}
}
}
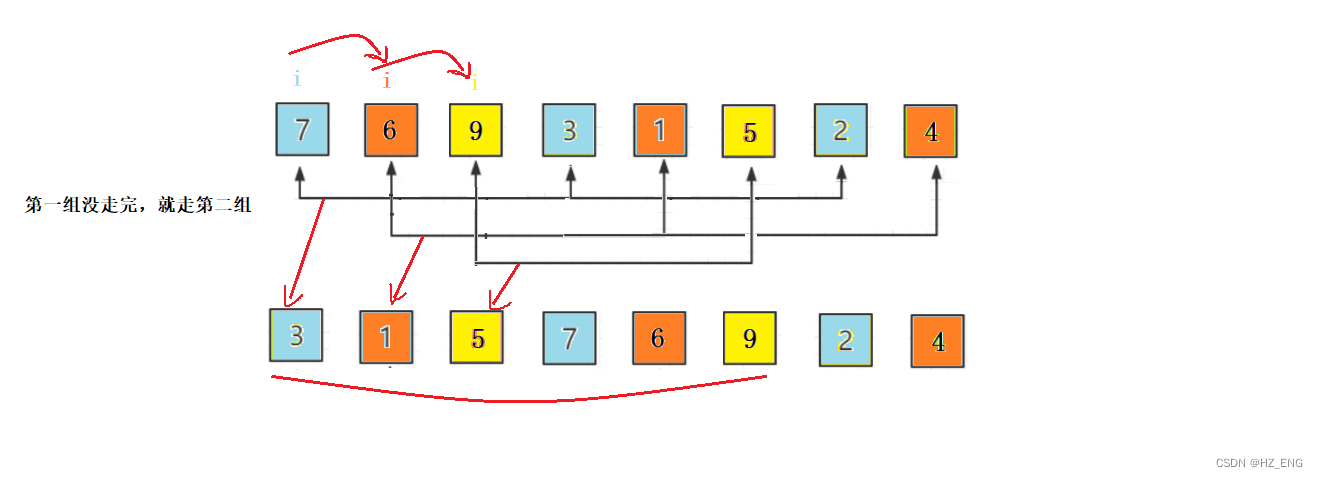
代码二: 一组走完,再走下一组
void ShellSort(int* a, int n)
{
int gap = n / 2; //增量初始值
//gap组进行插入排序
for (int j = 0; j < gap; j++)
{
for (int i = j; i < n - gap; i += gap) //对一组进行直接插入排序
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}
}
说明:代码一是对代码二的改进,并没有提升效率,两种方式在效率及性能上没有本质的区别。
时间和空间复杂度
时间复杂度: O(n^1.3)
空间复杂度: O(1)
说明:1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有 序的了,这样就会很快。这样整体而言,可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在一 些书中给出的希尔排序的时间复杂度都不固定
稳定性
希尔排序:不稳定排序。预排序时相同的数据可能分在不同的组