1. 摘要
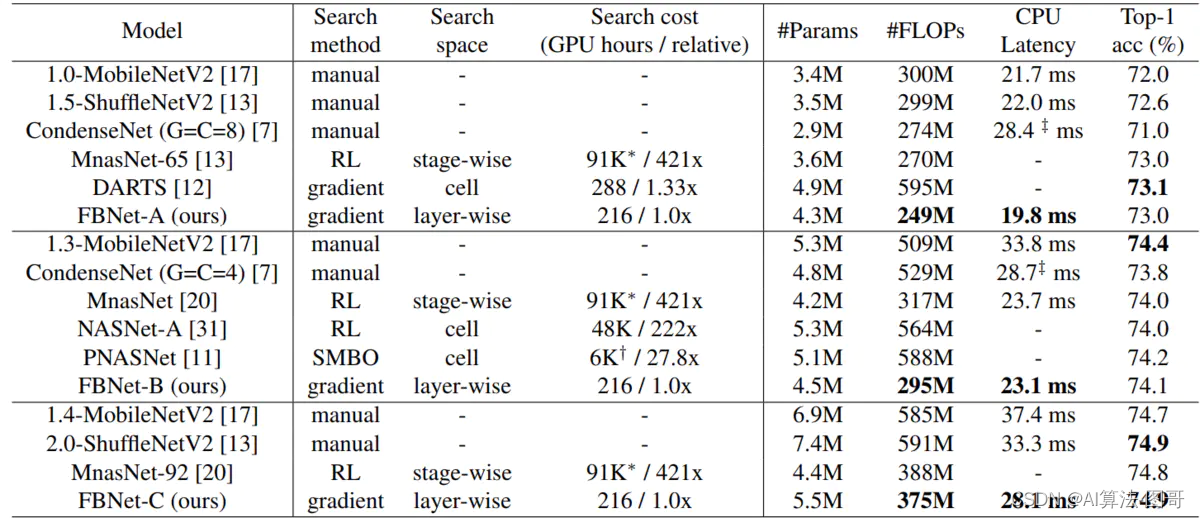
为移动设备设计卷积网络挑战巨大,因为设计空间巨大,现有NAS方法在计算上是昂贵的。另外,之前的工作关注降低FLOPs,但是FLOPs并不总是反应真实的延迟。因此基于differentiable neural architecture search(DNAS),采用梯度优化的方法优化卷积结构,避免像以前的方法那样分别枚举和训练各个体系结构。FBNets-B在ImageNet上top-1准确率为74.1%,295M FLOPs,在三星S8上23.1ms延迟,比MobileNetv2小2.4倍,快1.5倍。
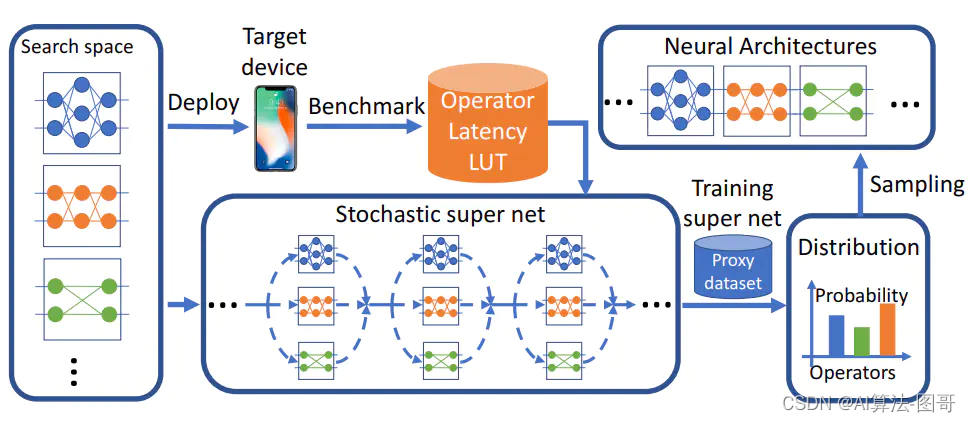
DNAS搜索一个层次空间,ConvNet的每一层都可以选择不同的块,搜索空间由一个随机超网络表示,搜索过程使用SGD训练随机超网以优化架构分布,从训练的分布中采样最佳体系结构。 在目标设备上测量每个操作的延迟并用于计算超网的损失。
2. 介绍
设计准确高效的ConvNet有如下挑战:
- 未知的设计空间,ConvNet的设计空间是组合的,训练ConvNet是非常耗时的,因此之前的网络设计基本不怎么搜索整个设计空间。采用强化学习和遗传算法的NAS非常耗时。
- 不可广泛移植的最优解,最优的卷积结构受很多因素限制,比如输入分辨率和目标设备。一旦这些因素改变,最优解的结构就会变化。
- 不一致的效率度量,大多数效率度量不仅依赖于网络结构也依赖目标设备的硬件和软件配置。之前的许多工作都用了硬件无关的度量比如FLOPs(乘加操作的次数)去评估效率。然而,FLOP计数低的网络不一定快。硬件无关的度量和实际的效率之间的不一致性使卷积网络的设计更加困难。
DNAS用操作随机执行的超级网络代表搜索空间,将找到最佳架构的问题放松到找到产生最佳架构分布的问题,通过使用Gumbel Softmax技术,可以直接基于梯度优化(SGD)的方法训练结构分布。用于训练随机超级网络的损失不仅仅是交叉熵损失,还包括延时损失。为了评估网络结构的延时,本文将计算搜索空间每个操作的延时并且使用速查表模型去计算所有操作的延时(每个操作的时间加起来),使用这个模型可以快速的估量庞大的搜索空间中网络结构的延时。更重要的是,它使得延时关于层结构选择是可微的。

3. 最近的工作
DARTS着重在cell级别的架构搜索,并且同样的cell结构重复堆叠得到网络整体,cell级结构是硬件不友好的,并且实际效率也很低。MnasNet研究了一个stage级的分层搜索空间,允许不同的block用于网络的不同stage,不过同一个stage中的block仍然是相同的。不同于关注FLOPs,[20]目的在于优化目标设备的延时。
4. 本文方法

4.1 搜索空间
之前的工作关注cell级别的搜索(单元级别),一旦单元结构搜索得到,网络就由这些单元堆叠得到。但是,许多搜索得到的单元结构非常复杂和琐碎,因此在移动端前向速度很慢。而且,同一结构的单元在不同深度回会网络的精度和延时有不同影响,因此本文允许不同的层选择不同的blocks来获得更好的精度和延时。
本文建立一个层次级别的搜索空间,其宏观结构固定,每层可以选择不同的block,整体结构如下图,Block这一列代表着block的类型,“TBS”表示需要被搜索层类型,f列代表着一个Block中卷积核的个数,n列代表着Block的个数,s列代表着第一个Block的stride。1504(1984)代表卷积的个数。
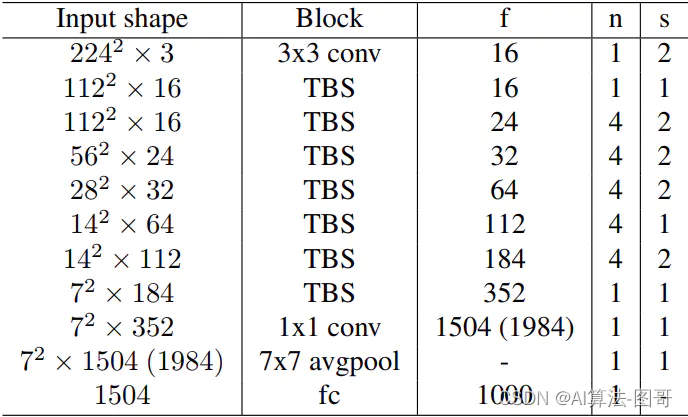
网络整体结构确定了网络层数和每层的输入输出的维数。网络的前三层和最后三层有着固定的操作。对于剩下的层,他们的Block需要被寻找。每层的卷积核个数是人为预先确定好的,对于浅层,使用相对较小的通道数,因为浅层的特征图分辨率较大,FLOP与输入尺寸的二次幂成正比。
网络中的每个可搜索层可以从层次搜索空间中选择不同的块,Block的结构来源于MobileNetv2和ShiftNet,如下图:包含1x1的point-wise卷积,KxK的depthwise卷积,以及一个1x1的point-wise卷积,ReLU函数跟在第一个1x1卷积和第二个KxK卷积之后,最后一个1x1卷积之后不接激活函数,如果输入分维度与输出分维度相同,则使用短路连接将输入与输出相加。同样仿照MobileNet-v2和ShiftNet以一个扩展比例来控制Block。它决定了第一个1x1卷积将输入特征图的通道扩大多少,对于Depth-wise卷积,卷积核的大小可以是3x3和5x5,对于第一个和最后一个的1x1卷积,使用group卷积(point-wise)来降低计算量。当使用group卷积时,仿照ShuffleNet来进行通道信息融合。
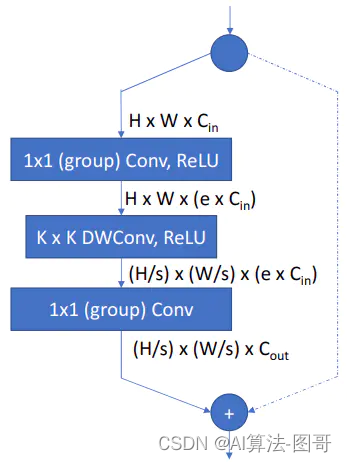
在实验中,层级的搜索空间包含9个候选Blocks,它们的设置如表:
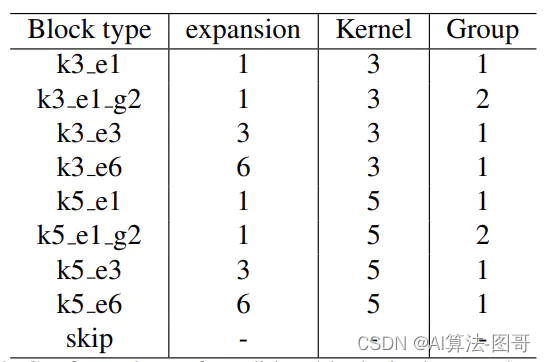
skip表示直接将输入特征图输出而不经过任何操作。候选Block可以帮助降低网络的深度。整体来看,搜索空间包含22层,每层可以选择9中候选的Blocks。
4.2 损失函数
损失函数定义为
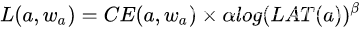
包含结构与参数的交叉熵损失,以网络在目标设备上的延时损失。我们不可能去对所有的网络结构进行延时测试,为了简化问题,使用一个延时速查表模型来评估整个网络的延时(基于每个操作的延时),因此:
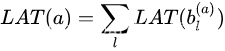
其中,
b
l
(
a
)
b_l^{(a)}
bl(a)代表结构a的第l层,每个操作的延时是独立于其他操作的。使用这样的方法,使得掩饰对于Block的选择是可微的,因此可以使用SGD来进行优化。
4.3 搜索算法
为了降低计算复杂度,有些算法将内层问题替换为在简单的数据集(CIFAR-10)上训练候选结构,尽管如此,训练依然是耗时的。
本文首先将搜索空间表示为一个随机的超级网络。这个超级网络有着上表所示的整体结构,每层包含9个上表所示并行的Blocks,在超级网络的前向过程中,只有一个候选的Block被采样进来,并以以下采样概率执行:
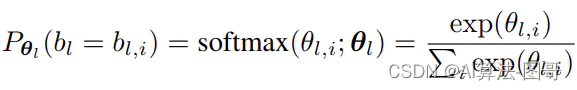
包含着决定第l层采样每种Block的概率的参数,第l层的输出为
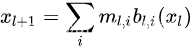
m
l
,
i
=
1
m_{l,i}=1
ml,i=1表示Block
b
l
,
i
b_{l,i}
bl,i被采样,否则为0,
b
l
,
i
(
x
l
)
b_{l,i}(x_l)
bl,i(xl)表示第层的第个Block的输出(给定输入特征图
x
l
x_l
xl),每层独立采样,因此结构可以定义为:
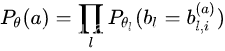
,是由组成的向量(第层的第个Block),
b
l
,
i
a
b^a_{l,i}
bl,ia表示在采样的结构a中,第l层选择第i个Block。重写优化问题的表达形式:
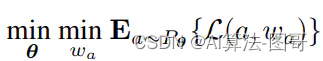
其中的损失函数对于权重
w
a
w_a
wa明显可微,可以采用SGD解决,但是该损失对于抽样参数
θ
\theta
θ并不是直接可微的,因为梯度不能由变量
m
l
,
i
m_{l,i}
ml,i 传递至
θ
l
,
i
\theta_{l,i}
θl,i,为了避开这个问题,将离散随机变量
m
l
,
i
m_{l,i}
ml,i扩展为:
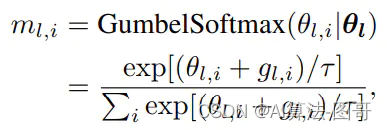
其中,
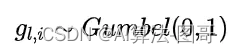
是一个服从Gumbel分布的随机噪音。
对于延时损失,使用速查表进行效率估计,因此:
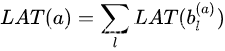
写作
L
A
T
(
a
)
=
∑
l
∑
i
m
l
,
i
L
A
T
(
b
l
,
i
)
LAT(a)=\sum_{l}\sum_{i}m_{l,i}LAT(b_{l,i} )
LAT(a)=∑l∑iml,iLAT(bl,i)
每个操作的延时是常数,因此整体延时对都是可微的,因此损失函数对于权重和结构分布参数都是可微的,因此可以使用SGD解决。
搜索过程等价于去训练随机super net。训练过程中,计算:损失对于权重的偏导数,去训练super net中每个操作f的权重,这部分与传统的卷积神经网络没有分别,操作搜索训练完城后,不同的操作使得整体网络的精度和速度不同,因此计算损失对于网络结构分布的偏导数,去更新每个操作的抽样概率。这一步会使得网络整体的精度和速度更高,因为抑制了低精度和低速度的选择,super net训练完成之后,可以从结构分布中抽样获得最优的结构。
5. 实验