前言:排序作为数据结构中的一个重要模块,重要性不言而寓,我们的讲法为下理论掌握大致的算法结构,再上代码及代码讲解,助你一臂之力。
一,冒泡
冒泡排序应该是大家学习以来第一个认识的排序方法,它的思想也是简单暴力,从第一元素开始每一个元素和前一个元素比较,如果不符合顺序就交换位置,直到最后一个元素,每一趟排序都可以排出那趟中一个最大的值并将它放到末尾位置
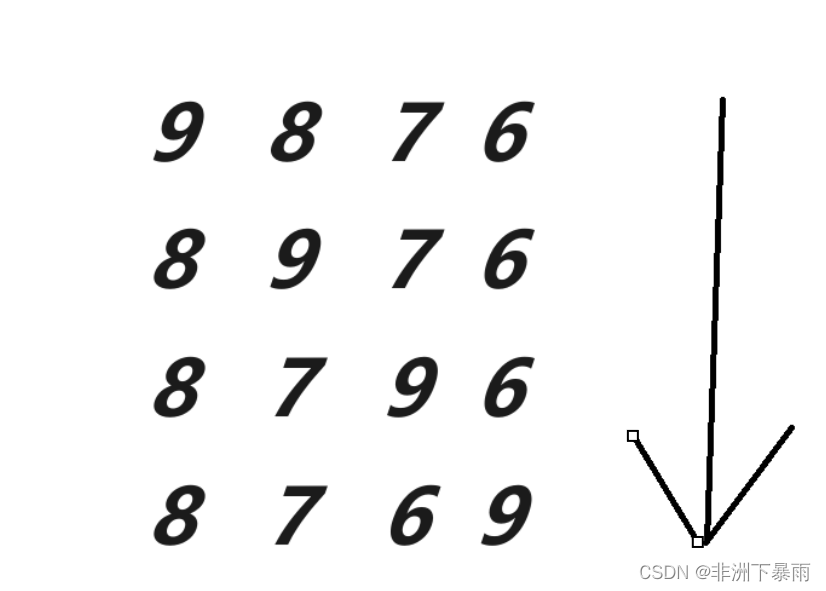
这是第一趟排序,第二次排序的话因为最后一个元素的位置已经排好了,所以可以少排一个元素

最后一趟就两个元素了,自然简单

最后得到 6 7 8 9。排序就成功啦
void BubbleSort(int* a, int n) {//n是数组的元素个数
for (int i = n - 1; i > 0; i--) {//外层循坏,因为每次只能拍好一个元素,所以需要排多次
for (int j = 0; j < i; j++) {//内层循坏,每次两两比较
if (a[j] > a[j + 1])
swap(a + j, a + j + 1);//交换函数
}
}
}二,选择排序
选择排序相较于冒泡排序更加简单,它的核心思想是每次从序列中选出一个最大的和最小的,然后继续比较中间的序列,直到序列就一个元素
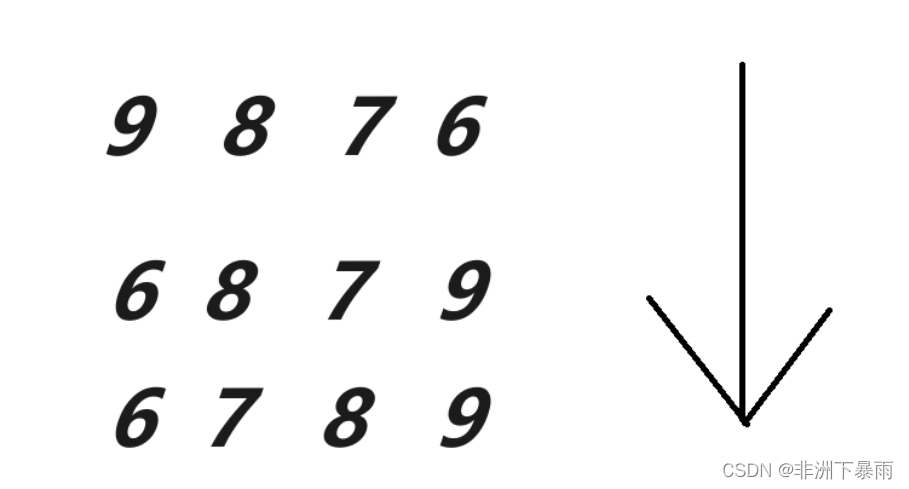
注意它和冒泡排序之间的差距,冒泡排序每趟排序可能对数组进行了大改动,而选择排序只会交换最大和最小以及它们应该所处的位置。但它们都有相同点,时间复杂度都是O(n^2)。
选择有一个大坑,可能我们初写是想不出来的,但最后结果会让我们失败。先看一组排序,我们不进行改良,用原思路解决

这是为什么呢,不难看出是因为MAX处于了一个特殊位置,导致max的位置发生了改变,达不到我们预期的特点,那我们应该怎么解决呢,答案就算加一个判断和更新,看我接下来的代码
void SelectSort(int* a, int n) {
int max, min;
int k = n;
for (int i = 0; i < k; i++, k--) {//外层循坏,每次少排两个元素
max = i;//先让max和min都赋值为第一个元素
min = i;
for (int j = i+1; j < k; j++) {//内层循坏,每次排出两个元素的位置
if (a[j] > a[max])//对大小值更新
max = j;
if (a[j] < a[min])
min = j;
}
if (max == i)//如果max处于特殊位置,我们就提前交换更新位置,防止出错
max = min;
swap(a + min, a + i);
swap(a + max, a + k - 1);
}
}三,插入排序
插入排序有一点像冒泡排序但是它们还是有一定的差距,插入排序是也是每趟将一个元素放到它应该所处的位置,但它是每个元素和前面一个元素进行比较,如果顺序不符合就交换,如果交换之后还不符合的话就继续交换,直到处于它与前面的元素不符合交换条件。
插入排序像一个跳级生,直到处于自己应该属于的位置,而冒泡排序稳扎稳打,每次都会全部比较。因此再大多数情况下插入排序会优于冒泡排序。

void InsertSort(int* a, int n) {
for (int i = 1; i < n; i++) {//外层循坏,每次会排好一个元素
int j = i;
while (a[j] < a[j - 1]) { //如果和前面元素比较结果不符合要求,就不断交换直到位置正确
swap(a + j, a + j - 1);
j--; //像前面推进,方便比较
}
}
}希尔排序前言:我们来思考一个问题,插入排序啥时候效率最好,啥时候最坏呢,从上面代码我们可以看出来,外层循坏我们是无法改变的,我们能改变的就是内层循坏,那我们如何减少内存排序的次数呢?没错就是内存循坏条件不符合,另一个方面来说就是让序列排序之前尽量接近有序,如果元素接近有序,它的时间复杂度就会接近O(n)。这个优化之后就是希尔排序啦
四,希尔排序
在上段话中我们可以知道当数据接近有序的话,那么插入排序的效率就越快,那如果我们该如何让数据接近有序呢?这里我们借鉴插入排序,我们如果把数据把数据间隔为gap的数据分为一组,并且对它们进行排序,最后K逐渐减小(一般默认gap初始值为n/2,每次减半),当gap=1时就是一个完全的插入排序,而之前的排序已经将数据进行预排序,因此最后一次排序的时间复杂度会小于O(n^2)。到底它的时间复杂度会为多少,这个涉及到了数学知识,不过我们的先辈大概算出来范围为O(n^1.3)。这有时一个优秀的排序算法,接下来我们看图掌握细节。
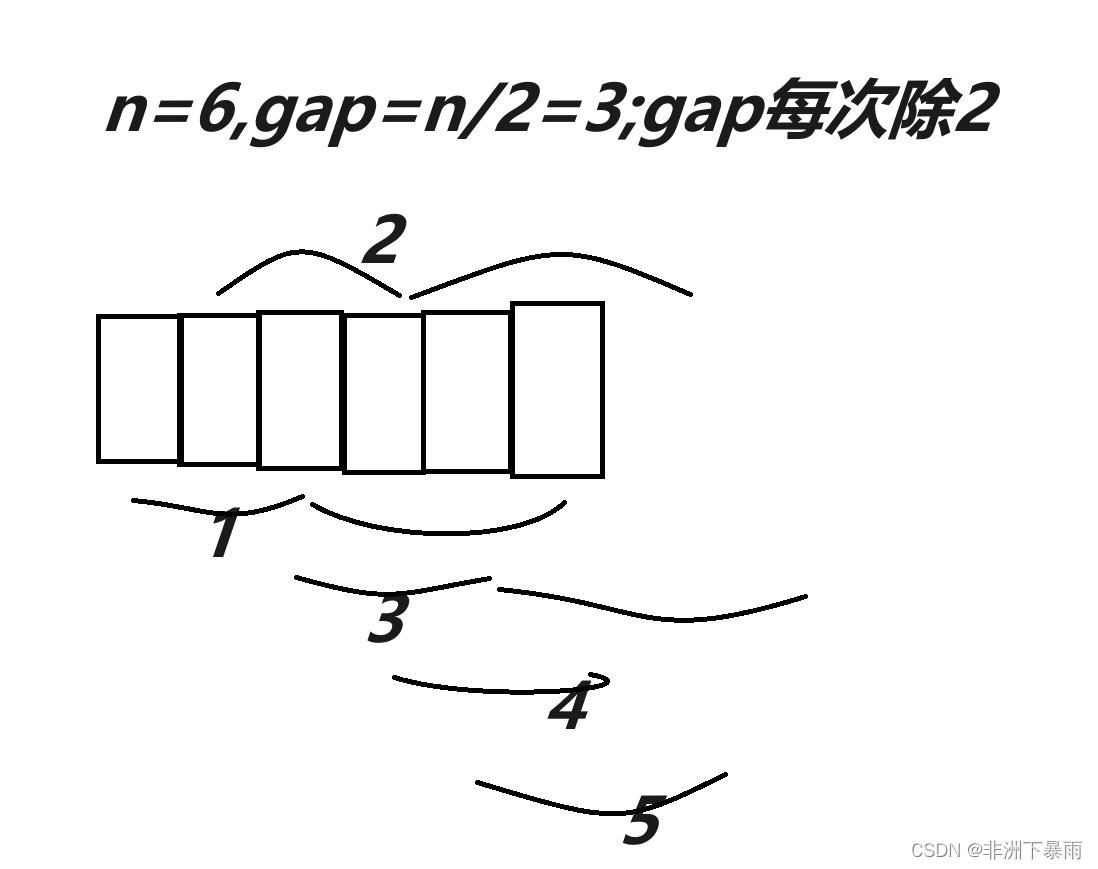
这个就是间隔为gap的值进行插入排序,每次gap值除2,这样可以尽量把大的数据带到前面(或者把小的数据带到前面,),把小的数据带到后面。相当于预排序了,最后一次完全插入排序就只是作为补充和检查,不会出现每次都要交换到头。
void ShellSort(int* a, int n) {
int gap = n / 2;//设置gap值
for (int i = gap; i > 0; i /= 2) {//i=gap,每次除2
for (int j = i; j < n; j++) {//从gap位置开始,每次和前面距离为gap的距离比较并适当交换
int k = j;
while (k - i >= 0) { //这个只是为了交换到0,函数里面有如果不符合就会跳出循坏的语句
if (a[k] < a[k - i])
swap(a + k, a + k - i); //不符合就交换,循坏继续
else break; //符号就跳出
k -= gap; //间隔为gap为一组
}
}
}
}五,堆排序
我以前写的文章链接CSDN
六,快排两种改良及非递归实现、
快排我们可能在C的库中见过并且用过,那么它的思想是怎么样的呢?快排是每次只排好一个数据,把大于这个数据的元素放到它的一边,小于它的数据放到另一边,然后把左右分别排好,那么具体怎么实现呢?快排会每次选取一个数据作为标记数据,这个数据一般是要进行筛选,防止取到了最大值和最小值,如果取到了的话,那么它的时间复杂度会到O(n^2),这个大家可以先听完再去思考为什么时间复杂度会上升。取到之后,我们的第一种思想是从数组左右开始比较,左边找到一个大于这个数据的值,右边找到一个小于这个数据的值,然后交换两个数据的值,最后交换标记数据和左右相遇的位置。
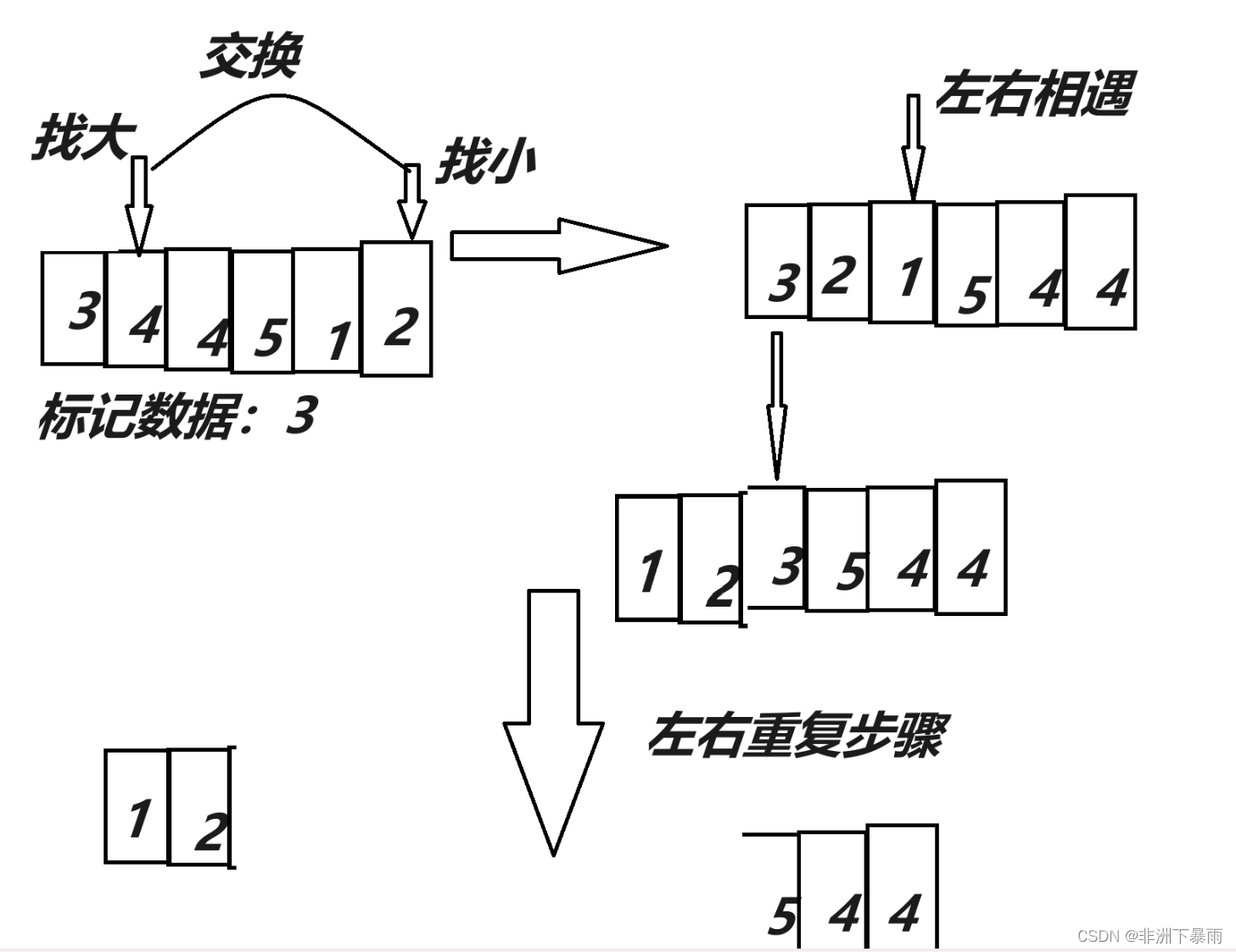
接下来看第一种思路的代码实现
int PartSort1(int* a, int left, int right) {
if (left >= right)
return;
int mid = Middlenum(a, left, right, (left + right) / 2);//三数取中
swap(a + mid, a + left); //将标记数据换到下标为0的位置
int left1 = left+1; //左右初始化
int right1 = right;
int key = left; //记录标记数据
while (left1 < right1) {
while (left1<right1 && a[right1]>=a[key])//找大
right1--;
while (left1<right1 && a[left1]<=a[key])//找小
left1++;
if(right1!=left1)
swap(a + right1, a + left1); //左右下标不相等交换
}
swap(&a[key], &a[right1]); //把标记数据放到应该处于的位置
PartSort1(a, left, left1-1); //左右数据递归处理
PartSort1(a, right1+1,right );
}有大佬觉得每次交换麻烦,于是想出来一种方法,我们直接把原来属于标记数据的位置再逻辑上变为一个坑,发现大于的数据就把数据挪到“坑”里面,交换坑和数据位置,其实就是覆盖,将坑的下标换为大于标记数据的位置,再找小于标记数据的位置,和坑交换,最后交换左右相遇位置和坑的位置,将标记数据放入坑里面,再左右递归即可。
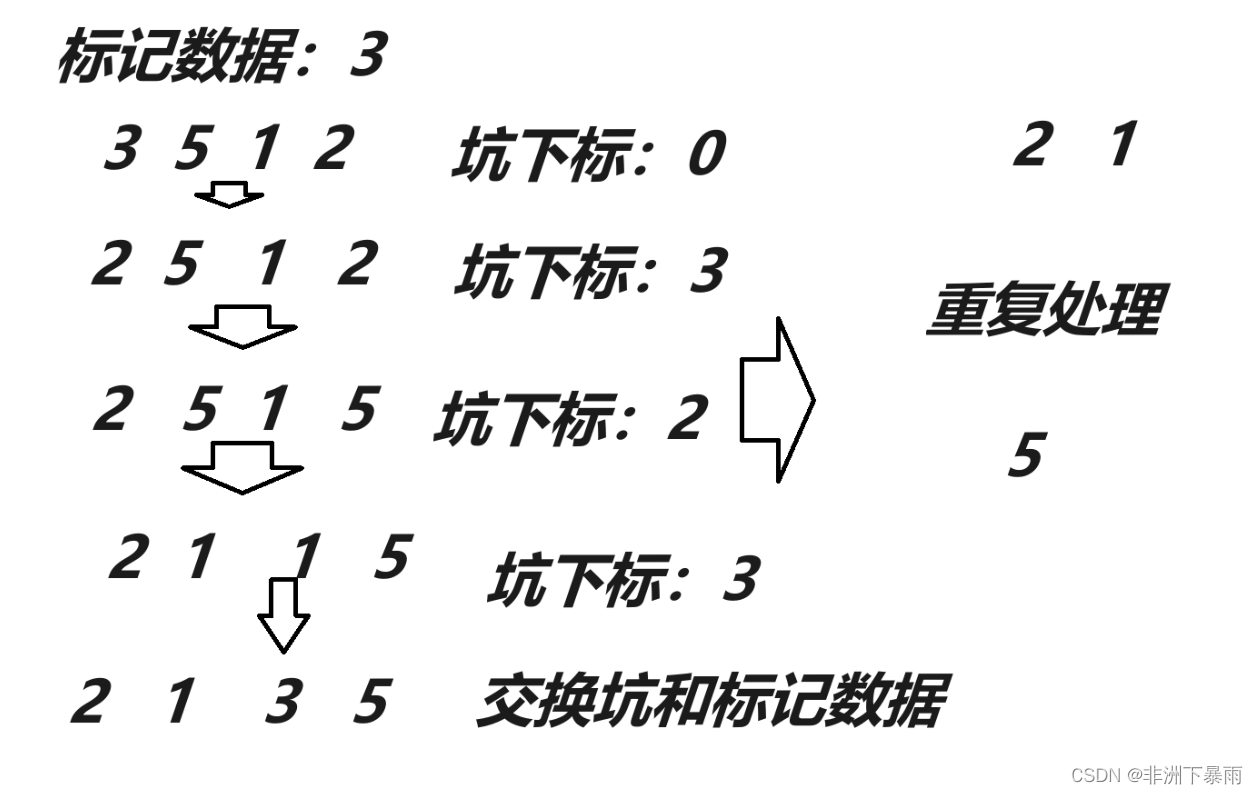
挖坑法代码实现:
int PartSort2(int* a, int left, int right) {
if (left >= right)
return;
int mid = Middlenum(a, left, right, (left + right) / 2);//三数取中
swap(a + mid, a + left); //将标记数据换到下标为0的位置
int left1 = left + 1; //左右初始化
int right1 = right;
int key = a[left]; //记录标记数据
int hole = left; //挖坑下标
while (left1 < right1) {
while (left1 < right1 && a[right1] >= key)//找大
right1--;
a[hole] = a[right1]; //和坑交换位置
hole = right1;
while (left1 < right1 && a[left1] <= key) //找小
left1++;
a[hole] = a[left1]; //和坑交换位置
hole = left1;
}
a[hole] = key; //把标记数据放入坑
PartSort1(a, left, left1 - 1); //左右递归排序
PartSort1(a, right1 + 1, right);
}第三种思路类似于推箱子,两个指针从非标记数据的第一个数据开始,把大于标记数据的值往后面推,小于标记数据的值往前面推,最后交换走的慢的那个指针位置和标记数据的值,因为此时恰好这个指针的前面是小于标记数据的值,后面是大于标记数据的值。

双指针法:
int PartSort3(int* a, int left, int right) {
if (left >= right)
return;
int mid = Middlenum(a, left, right, (left + right) / 2);//三数取中
swap(a + mid, a + left); //将标记数据换到下标为0的位置
int prv = left; //双指针位置初始化
int cur = left + 1;
int key = left;
while (cur <=right) { //防止快指针越界访问
if (a[cur] <=a[key] && ++prv != cur) //两个指针不相等时,并且找到了大于标记数据的值时交换
swap(a + prv, a + cur);
cur++;
}
swap(a + key, a + prv); //交换慢指针和标记数据的值
PartSort3(a, left, prv-1); //左右递归排序
PartSort3(a, prv+1, right);
}现在我们来讲非递归实现,为什么我们要将这个呢?这涉及到了电脑的内存分配,递归是要占用比较多的栈空间,而栈空间很小,因此我们不能过于利用栈空间,属于非递归就是解决这个问题。递归改非递归的核心就是根据思想模拟,比如递归我们可以参考栈,先进后出,我们也就是利用递归的思想来解决这个问题
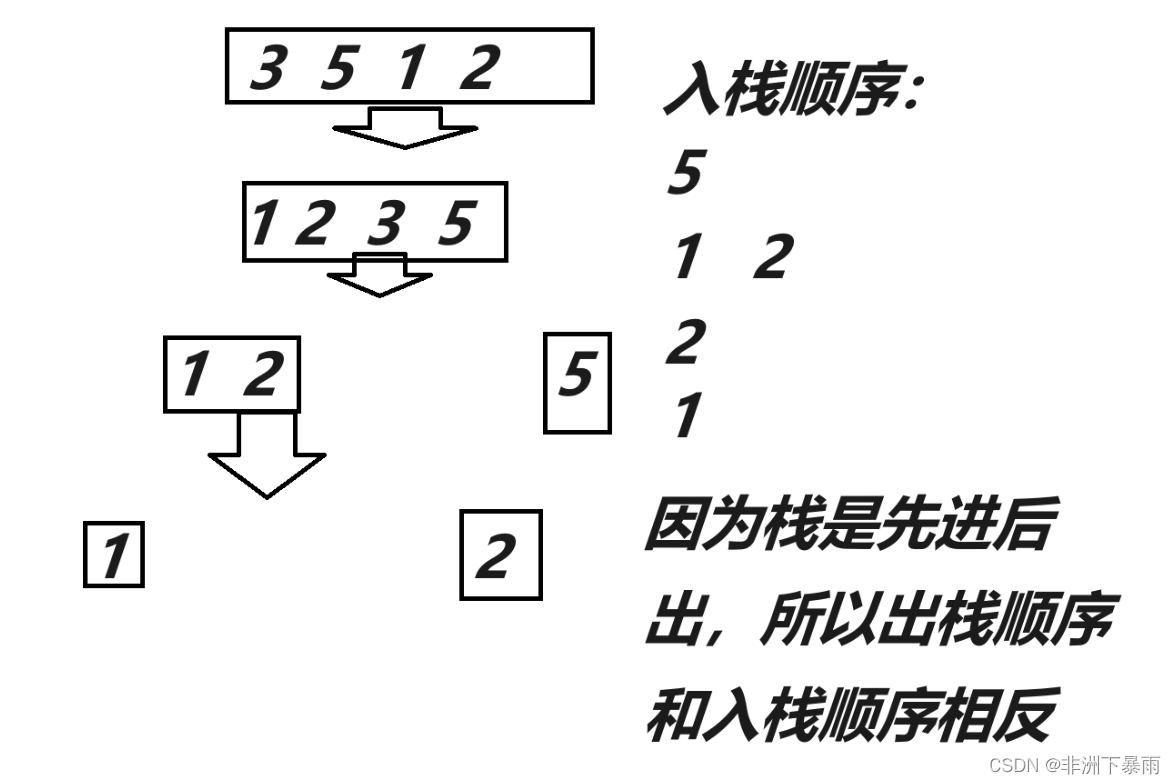
代码实现:
void QuickSortNonR(int* a, int left, int right) {
Stack* ps; //建栈
ps = (Stack*)malloc(sizeof(Stack));
StackInit(ps); //初始化栈
StackPush(ps, left); //把原始位置的左右下标入栈
StackPush(ps, right);
while (StackEmpty(ps)!=1) { //只要栈不为空就继续
int right1 = StackTop(ps); //把左右下标取出来并出栈
StackPop(ps);
int left1 = StackTop(ps);
StackPop(ps);
if (left1 >= right1) //对标记数据排序,省略注释,不理解看前面讲解
continue;
int mid = Middlenum(a, left1, right1, (left1 + right1) / 2);
swap(a + mid, a + left1);
int prv = left1;
int cur = left1 + 1;
int key = left1;
while (cur <= right1) {
if (a[cur] <= a[key] && ++prv != cur)
swap(a + prv, a + cur);
cur++;
}
swap(a + key, a + prv);
StackPush(ps, prv+1); //把排序之后的左右部分入栈
StackPush(ps,right1);
StackPush(ps, left1);
StackPush(ps, prv - 1);
}
}栈的代码及讲解:CSDN
快排时间复杂度讲解

此时是最理想的状态,每次排序刚刚好取到中间值,时间复杂度为nlogn
我们看最差的状态
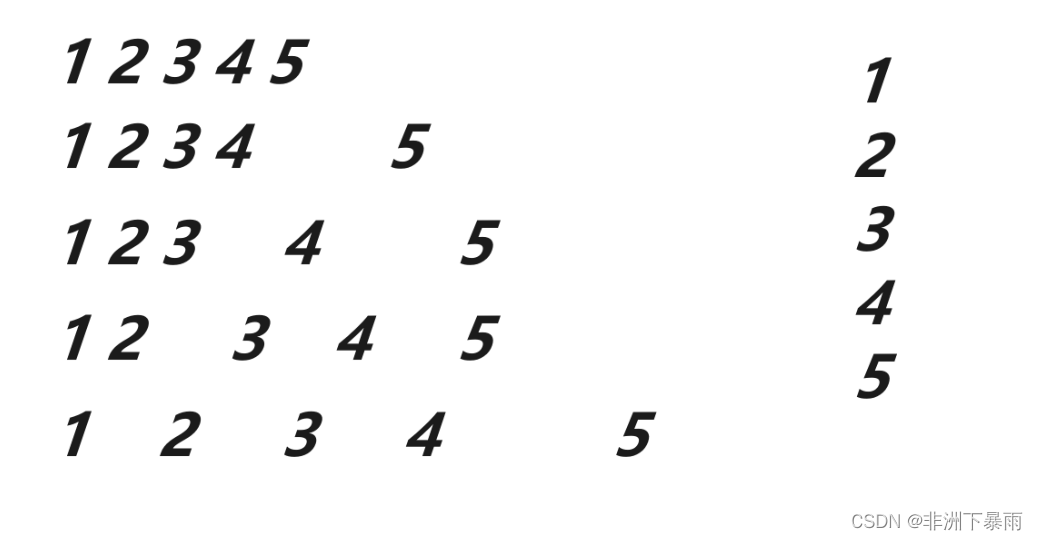
不难发现此时的时间复杂度为n^2,因此我们需要三数取中防止一直取到最大值或者最小值。
七,归并排序
归并排序我们不用文章描述,我们直接看图
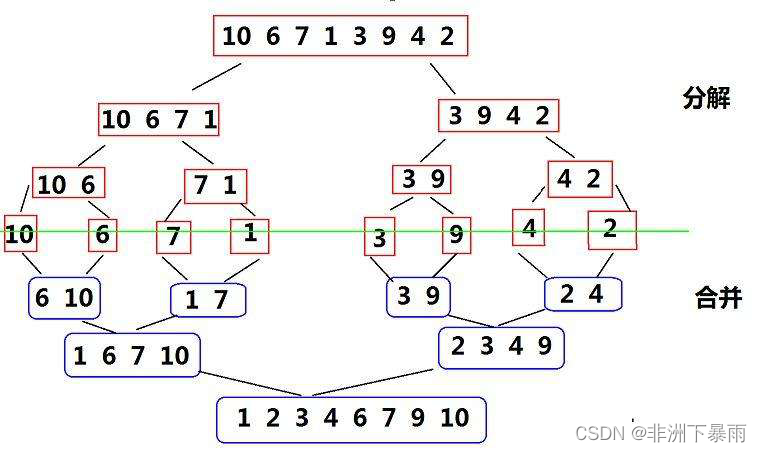
归并排序就是分解为一块快小块进行排序,然后将小快排序合并,中间有一个细节,我们不能边比较边改变原始数组,不然会将数组覆盖,无法比较成功,因此我们还需要一个额外的数组,我们来看代码
void MergeSort(int* a, int n) {
int* temp = (int*)malloc(sizeof(a));//开一个数组用来记录改变
Merge(a, temp, 0, n);
}
void Merge(int* a, int *temp,int left, int right) {
if (left + 1 < right) { //先进行左右递归排序分解为小块直到只有一个元素
Merge(a, temp, left, (left + right) / 2);
Merge(a, temp, (left + right) / 2+1, right);
}
if (left == right) //此时只有一个元素无法比较,直接返回
return;
int count = left; //接下来会用来标记
int mid = (left + right) / 2; //找到两需要排序数组的边界,作为接下来的循坏条件
int left1 = left; //寻找左右数组起始位置2
int right1 = (left+right)/2+1;
while (left1 <= mid && right1 <= right) { //越界就结束循坏
if (a[left1] < a[right1]) { //左右比较放进临时数组
temp[count++] = a[left1++];
}
else
temp[count++] = a[right1++];
}
while (left1 <= mid) //此时只有一个数组完全录入了临时数组,我们需要把另一个数组录入
temp[count++] = a[left1++];
while (right1 <= right)
temp[count++] = a[right1++];
memcpy(a + left, temp + left, (right-left+1)*4);//C语言库函数将改变的值复制回原数组,方便下一次排序
}非递归实现改怎么搞呢?我们这里不能用栈,因为归并排序是需要同层一层递归数据进行比较,显然栈是无法实现的,我们还是老老实实用循坏两两比较,设置一个gap值作为每个数组的大小,然后进行++,但是我们要考虑越界问题,还有gap每次乘2.
void MergeSortNonR(int* a, int n) {
int gap = 1; //gap值初始化
int* temp = (int*)malloc(sizeof(int) * n); //开辟临时空间作为中转
while (gap < n) { //只要gap小于数组大小就能比较
for (int i = 0; i < n; i += 2*gap) { //每一次比较可能有大于两个数字,所以要循坏直到没有数据
int left = i; //左右数组边界赋值
int right = i + gap;
int count=i; //标记临时数组的进度
while(right < n && left < i + gap && right < i + 2 * gap) { //只要不越界就继续比较
if (a[left] > a[right])
temp[count++] = a[right++];
else
temp[count++] = a[left++];
}
while (left < i + gap && left < n)//此时只有一个数组完全录入了临时数组,我们需要把另一个数组录入
temp[count++] = a[left++];
while(right < i + 2 * gap && right < n)
temp[count++] = a[right++];
memcpy(a + i, temp + i, (count - i) * 4);//C语言库函数将改变的值复制回原数组,方便下一次排序
}
gap *= 2;//gap值改变
}
}八,计数排序
计数排序人如其名,用数组就是记录每个数字出现的次数,利用数组特性,将数字按顺序直接放进去,我们需要记录最大值和最小值来确定数组的范围,所以我们返回原数组时需要加上最小值即可,但是计数排序有很明显的缺点,就是只能排整形,并且如果最大值和最小值差距过大会浪费很多空间。

void CountSort(int* a, int n) {
int max = a[0]; //寻找最大最小的变量
int min = a[0];
for (int i = 0; i < n; i++) { //循坏找到最大最小值
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int* arr = (int*)malloc(sizeof(int) * (max-min)); //开辟记录数组
memset(arr, 0, sizeof(int) * (max - min)); //C语言库函数数组全部初始化为0
for (int i = 0; i < n; i++)
arr[a[i]-min]++; //如果有这个数就对应位置加1
for (int i = 0, j = 0; i < n; i++) { //返回原数组,通过覆盖实现
while (arr[j] == 0)
j++; //先找到存在的数的位置
a[i] = j + min; //覆盖原始数组
arr[j]--; //覆盖之后就减减
}
}
博客创造不易,耗费颇多心血,如果你有收获希望点赞收藏加关注