题目列表
2864. 最大二进制奇数
2865. 美丽塔 I
2866. 美丽塔 II
2867. 统计树中的合法路径数目
一、最大二进制奇数

这题只要你对二进制有了解(学编程的不会不了解二进制吧),应该问题不大,这题要求最大奇数,1.奇数:只要保证二进制的最低位上是1就行(这里为不了解二进制的同学解释一下,二进制从低位到高位的权重分别是2^0,2^1,2^2...即除了最低位其他位都是偶数,所以最低位必须是1)
2.最大:贪心,我们将除了最低位的1之外的所有1都往高位放,得到的数肯定是最大的
代码如下
class Solution {
public:
string maximumOddBinaryNumber(string s) {
int cnt1=count(s.begin(),s.end(),'1');
return string(cnt1-1,'1')+string(s.size()-cnt1,'0')+'1';
}
};二、美丽塔I

这题的数据范围比较小,可以直接暴力,将每一个元素都当成山顶算一遍最大高度,然后比较得到最大高度,代码如下
class Solution {
public:
long long maximumSumOfHeights(vector<int>& maxHeights) {
long long ans=0;
int n=maxHeights.size();
for(int i=0;i<n;i++){
long long res=maxHeights[i];
for(int j=i-1,Min=maxHeights[i];j>=0;j--){
Min=min(Min,maxHeights[j]);
res+=Min;
}
for(int j=i+1,Min=maxHeights[i];j<n;j++){
Min=min(Min,maxHeights[j]);
res+=Min;
}
ans=max(ans,res);
}
return ans;
}
};三、美丽塔II
这题的题目和上一题一样,只是加大了数据范围,即不能用暴力枚举的方法解题,那么我们怎么优化算法呢?关键在于发现上面一题的算法中有什么是被重复计算的,我们只要减少这些无用的运算,就能实现算法的时间复杂度优化。
为了方便叙述,我将山顶前面的部分称为上坡,山顶后面的部分称为下坡,很显然,上面算法在每次计算上坡/下坡时,总是不断的遍历之前就已经遍历过的元素,那么我们如何根据已经遍历过的元素来求出当前的上坡/下坡的高度呢?而且上坡和下坡的计算是分开的互不影响的,只要我们提前处理出各种上坡和下坡的高度,我们就能在O(n)的时间里得到最大高度。
如何利用之前遍历的元素信息,得到当前的上坡/下坡的高度?以计算上坡为例,解析如下

代码如下
class Solution {
public:
long long maximumSumOfHeights(vector<int>& maxHeights) {
long long ans=0;
int n=maxHeights.size();
vector<long long>pre(n),suf(n);//分别代表以i为山顶的上坡和下坡
stack<int>st;//里面存放下标,方便计算出栈个数和索引高度
st.push(-1);//这里是为了方便计算,简化逻辑
for(int i=0;i<n;i++){
while(st.size()>1&&maxHeights[i]<maxHeights[st.top()])
st.pop();
int idx=st.top();
pre[i]=(idx<0?0:pre[idx])+1LL*(i-st.top())*maxHeights[i];
st.push(i);
}
st=stack<int>();//让栈为空
st.push(n);//这里是为了方便计算,简化逻辑
for(int i=n-1;i>=0;i--){
while(st.size()>1&&maxHeights[i]<maxHeights[st.top()])
st.pop();
int idx=st.top();
suf[i]=(idx==n?0:suf[idx])+1LL*(st.top()-i)*maxHeights[i];
st.push(i);
}
for(int i=0;i<n;i++){
ans=max(ans,pre[i]+suf[i]-maxHeights[i]);
}
return ans;
}
};这里说明一下算法的时间复杂度为O(n),有人或许看到求pre/suf中有两层循环,就认为时间复杂度为O(n^2),但其实不是,我们来看一下while循环里面的出栈语句执行了多少次,因为我们入栈的元素是n个,所以出栈的元素也只能是n个,所以这条语句只能执行n次,所以时间复杂度为O(n)
四、统计树种的合法路径数量
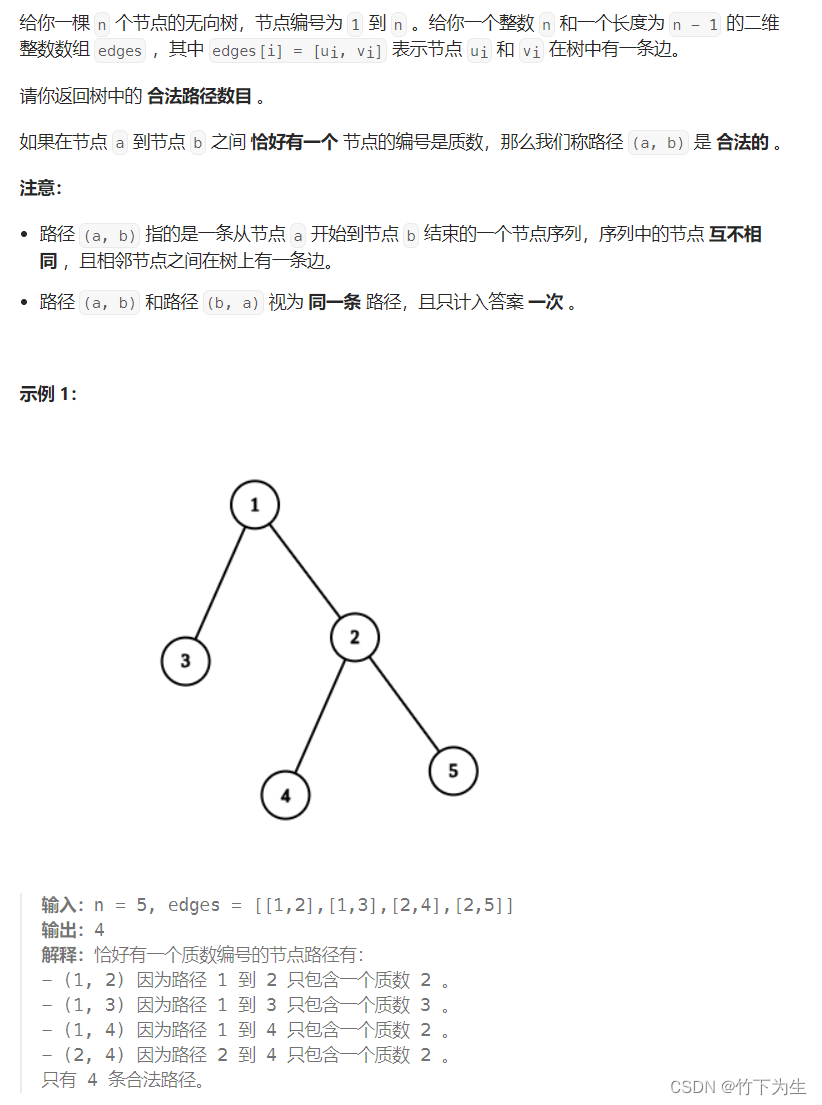
这题求路径个数,首先读懂题意,要求路径上包含一个质数,那么我们是从质数出发好,还是从非质数出发好呢?我们只要稍稍想一下就会发现从质数出发好,因为这样我们只要找到下一个质数就停止,而从非质数出发,我们就需要连续找到两个质数,很显然从非质数出发要处理的情况更多,所以我们从质数出发找路径,当然注意这题的路径至少需要两个结点(看示例一)
那么我们从质数出发怎么算呢?(判断质数就不讲了,不会的可以去看Leetcode-352周赛的第二题)
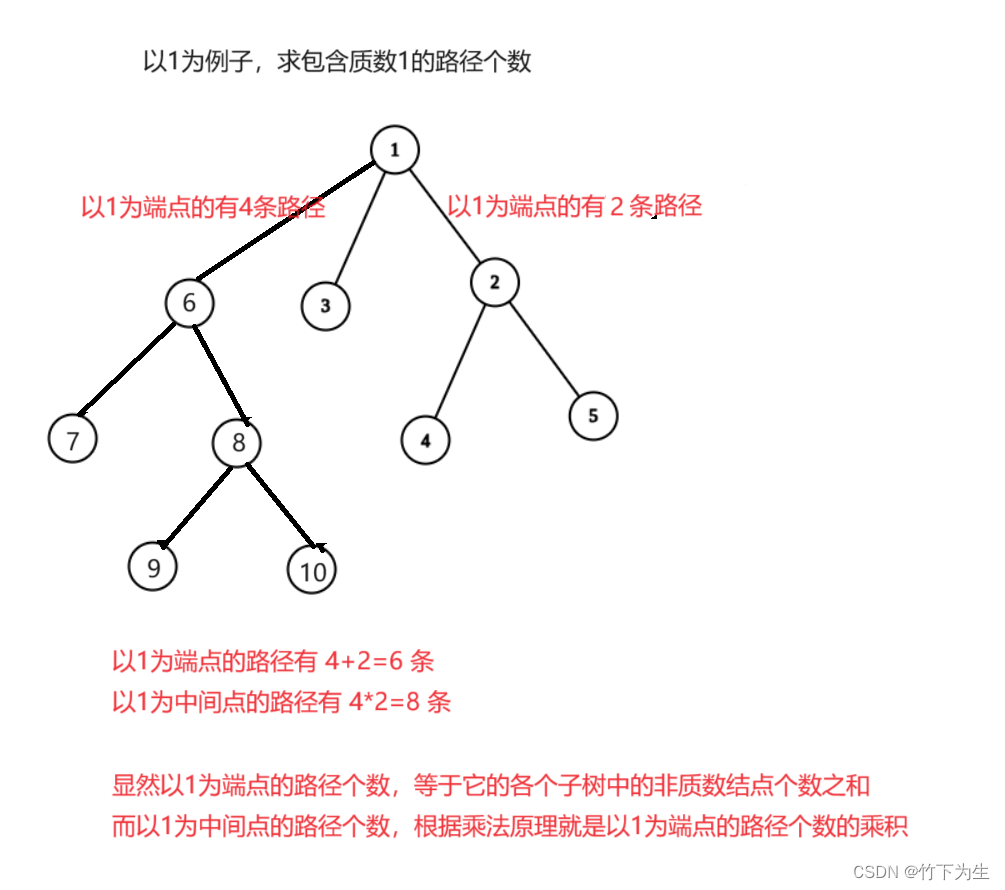
其他的路径求解方法同上,代码如下
//埃氏筛
const int MX=1e5;
vector<bool>is_prime(MX+1,true);
int init=[](){
is_prime[1]=false;
for(int i=2;i*i<=MX;i++){
if(is_prime[i]){
for(int j=i*i;j<=MX;j+=i){
is_prime[j]=false;
}
}
}
return 0;
}();
class Solution {
public:
long long countPaths(int n, vector<vector<int>>& edges) {
vector<vector<int>>g(n+1);
for(auto&e:edges){
int x=e[0],y=e[1];
g[x].push_back(y);
g[y].push_back(x);
}
//计算质数结点连接的每一个子树中的非质数结点个数
vector<int>sz(n+1);
vector<int>nodes;
function<void(int,int)> dfs=[&](int x,int fa){
nodes.push_back(x);
for(int y:g[x])
if(y!=fa&&!is_prime[y])
dfs(y,x);
};
long long ans=0;
for(int x=1;x<=n;x++){
if(!is_prime[x]) continue;
int sum=0;
for(int y:g[x]){
if(is_prime[y]) continue;
if(sz[y]==0){
nodes.clear();
dfs(y,-1);
for(int z:nodes){
sz[z]=nodes.size();
}
}
ans+=(long long)sum*sz[y];//以i为中间点的路径
sum+=sz[y];
}
ans+=sum;//以i为端点的路径
}
return ans;
}
};