给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
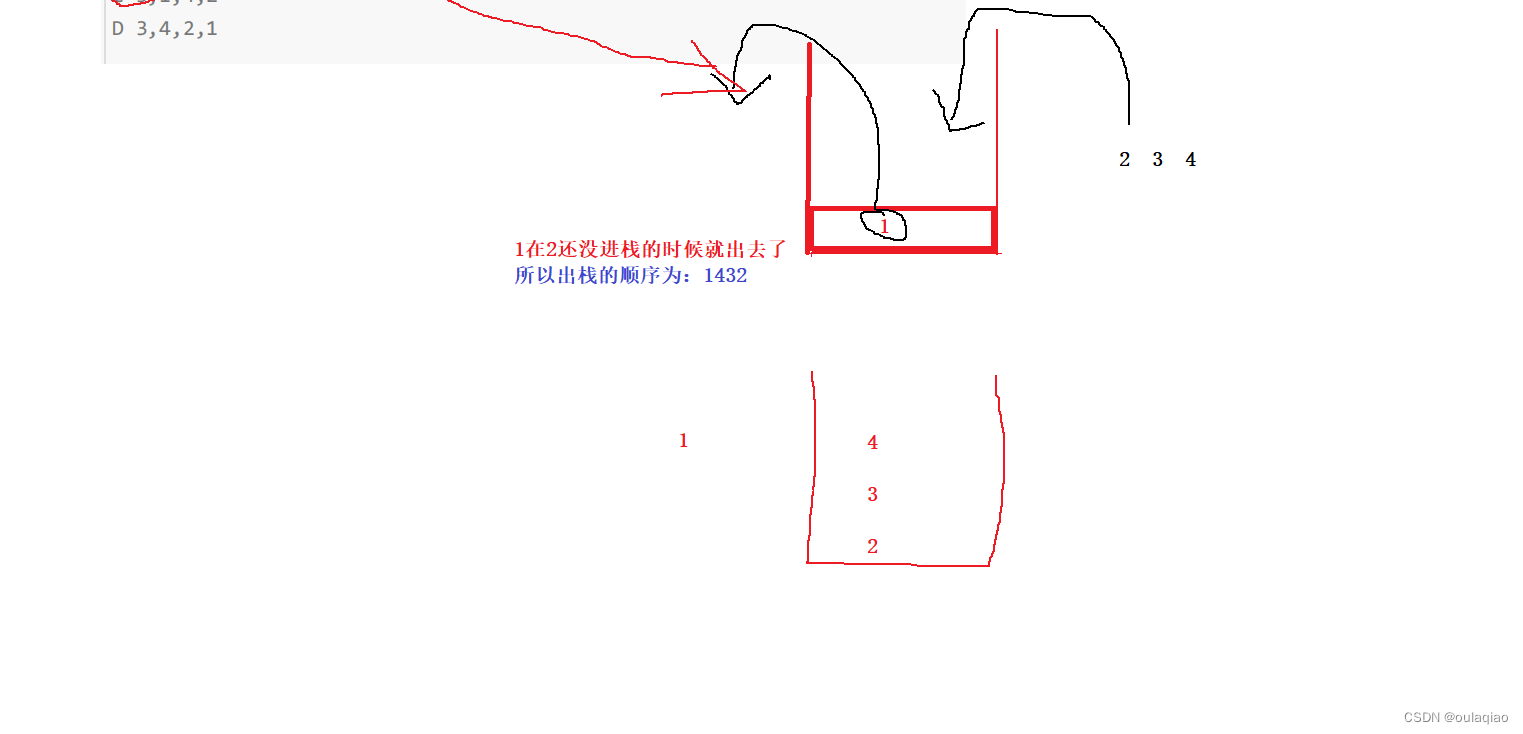
输入:n = 12 输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13 输出:2 解释:13 = 4 + 9
>>思路和分析
可以这样看这道题:完全平方数看成是物品(可以无限件使用),凑成正整数n就是背包,问凑满这个背包最少有多少个物品?那么就可以用动态规划:322.零钱兑换的完全背包思路来解决此题~
>>动规五部曲
1.确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j]
2.确定递推公式
- dp[j] 可以由dp[i - i * i]推出,dp[j - i * i] + 1便可以凑成dp[j],此时我们可以选择最小的dp[j]
- 递推公式:dp[j] = min(dp[j - i * i] + 1,dp[j]);
3.dp数组初始化
(1)dp[0] = 0;
- 没有意义,因为题目描述中,找到若干个完全平方数(比如1,4,9,16,...),题目描述中没有说要从0开始,dp[0] = 0 完全是为了递推公式
(2)非0下标的dp[j]一定要初始为最大值
- 因为从递推公式dp[j] = min(dp[j - i * i] + 1,dp[j]);中可以看出每次dp[j]都要选择最小的,为了避免dp[j]在递推的时候被初始值覆盖的可能,有必要将非0下标的dp[j]初始为最大值
4.确定遍历顺序
- 方式一:先遍历物品再遍历背包(求组合数)
- 方式二:先遍历背包再遍历物品(求排列数)
本题中所求为钱 的完全平方数的最少数量 ,与顺序无关。所以可以方式一或者方式二都可以!!
5.举例推导dp数组
已输入n为5为例,用方式一的遍历顺序,即先遍历物品再遍历背包,dp状态如下:

(1)用方式一进行遍历:
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i * i <= n; i++) { // 遍历物品
for (int j = i * i; j <= n; j++) { // 遍历背包
dp[j] = min(dp[j - i * i] + 1, dp[j]);
}
}
return dp[n];
}
};- 时间复杂度: O(n * √n)
- 空间复杂度: O(n)
(2)用方式二进行遍历:
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1,INT_MAX);
dp[0] = 0;
for(int j=0;j<=n;j++) { // 背包
for(int i=1;i*i <= n;i++) { // 物品
if(j>=i*i)
dp[j] = min(dp[j],dp[j - i*i] + 1);
}
}
return dp[n];
}
};- 时间复杂度: O(n * √n)
- 空间复杂度: O(n)
参考和推荐文章、视频:
代码随想录 (programmercarl.com)动态规划之完全背包,换汤不换药!| LeetCode:279.完全平方数_哔哩哔哩_bilibili
来自代码随想录的视频截图: