1.算法思想
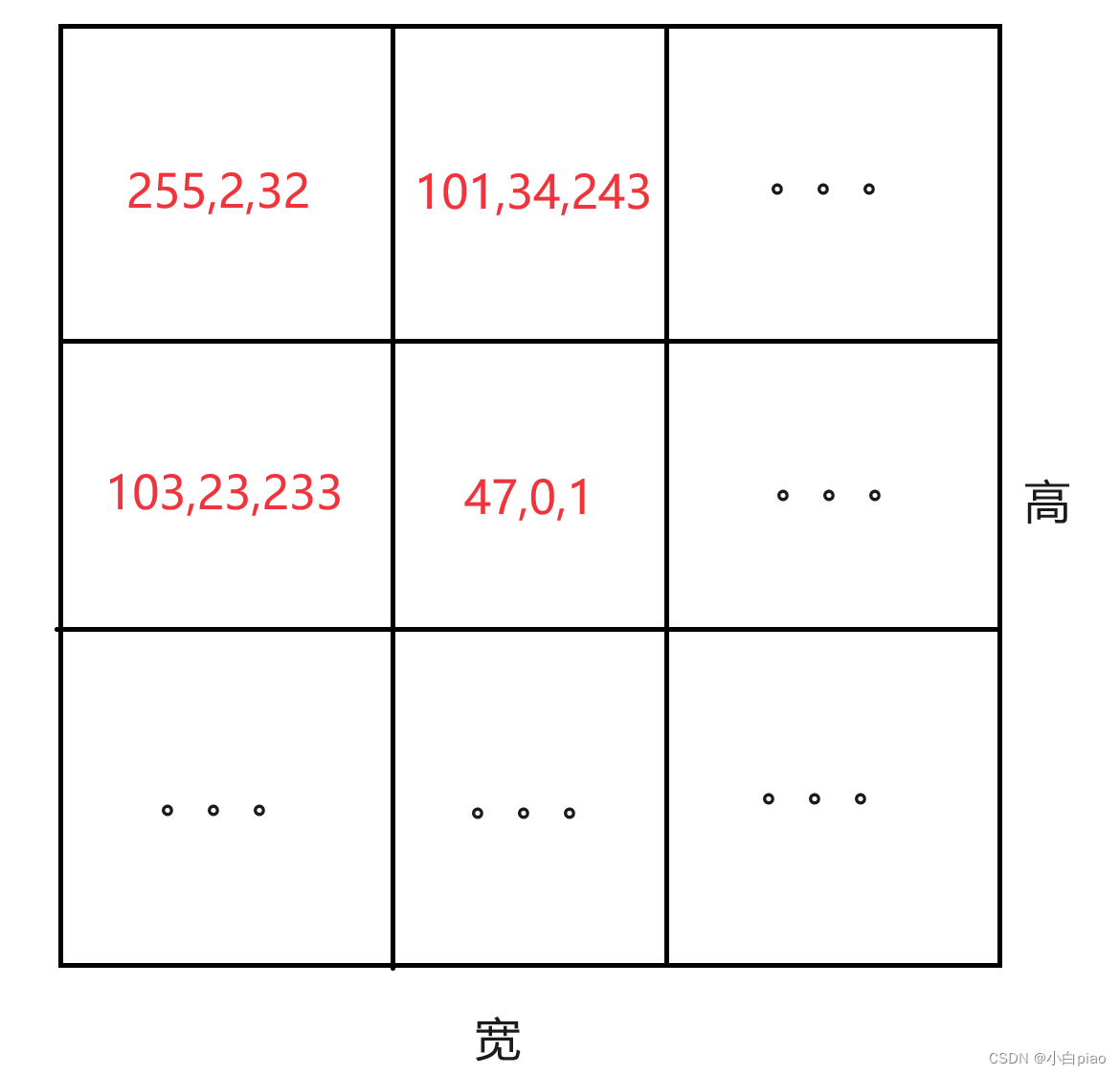
假设长度为n的线性表中每个结点aj的关键字由d元组
(
k
j
d
−
1
,
k
j
d
−
2
,
k
j
d
−
3
,
.
.
.
,
k
j
1
,
k
j
0
)
(k_{j}^{d-1},k_{j}^{d-2},k_{j}^{d-3},... ,k_{j}^{1} ,k_{j}^{0})
(kjd−1,kjd−2,kjd−3,...,kj1,kj0)组成,
其中,
0
<
=
k
j
i
<
=
r
−
1
(
0
<
=
j
<
n
,
0
<
=
i
<
=
d
−
1
)
0<=k_{j}^{i}<=r-1(0<=j<n,0<=i<=d-1)
0<=kji<=r−1(0<=j<n,0<=i<=d−1),r称为“基数”。
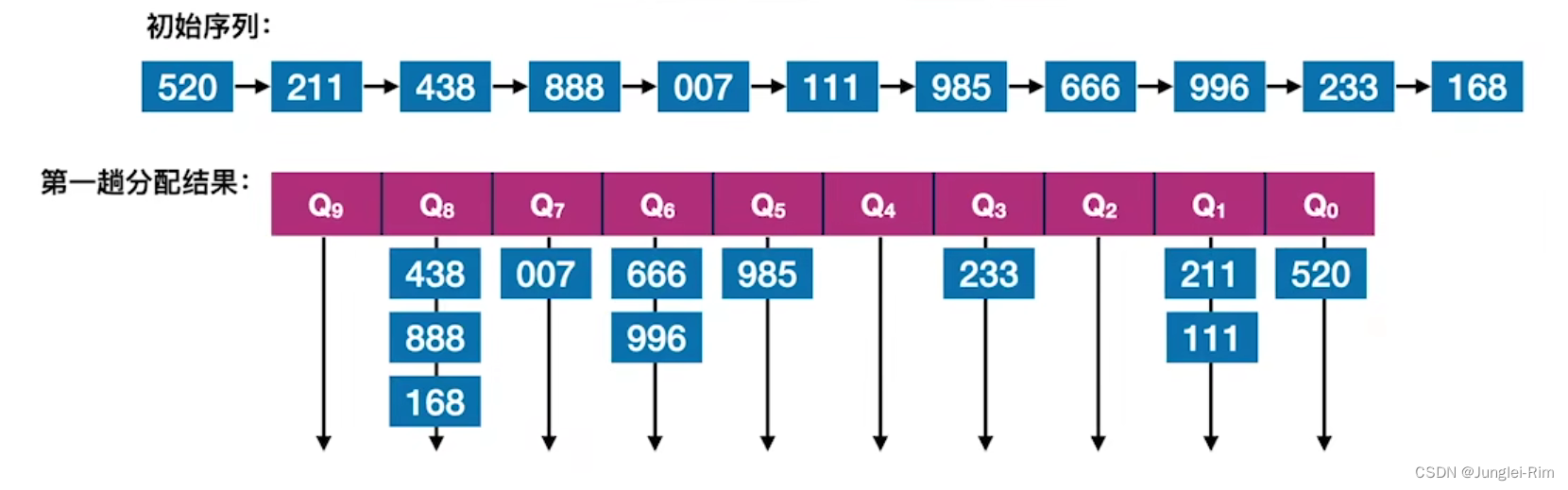
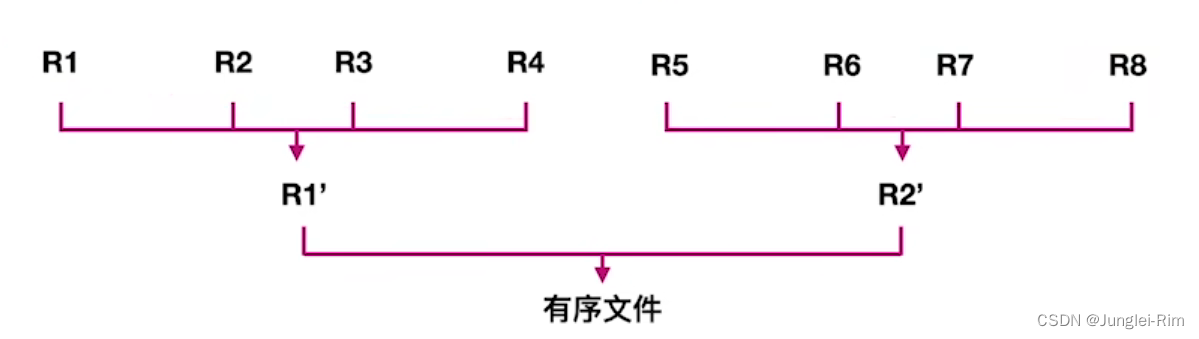
基数排序得到递减序列的过程如下:
- 初始化︰设置r个空队列, Q r − 1 , Q r − 2 , . . . , Q 0 Q_{r-1},Q_{r-2,}...,Q_0 Qr−1,Qr−2,...,Q0
- 按照各个关键字位权重递增的次序(个、十、百),对d个关键字位分别做“分配”和“收集”
- 分配:顺序扫描各个元素,若当前处理的关键字位,则将元素插入Qx队尾,一趟分配耗时O(n)
- 收集:把 Q r − 1 , Q r − 2 , . . . , Q 0 Q_{r-1},Q_{r-2},...,Q_0 Qr−1,Qr−2,...,Q0各个队列中的结点依次出队并链接,一趟收集耗时O(r)
例如:收集:得到一个按“百位”递减排列的序列,若“百位”相同则按“十位"递减排列,若“十位”还相同则按“个位”递减排列。
基数排序不是基于“比较”的排序算法。
2.算法效率分析
基数排序通常基于链式存储实现:
typedef struct LinkNode {
ElemType data;
struct LinkNode *next;
} LinkNode, *LinkList;
链式队列设计:
typedef struct {//链式队列
LinkNode *front, *rear;//队列的队头和队尾指针
} LinkQueue;
1.空间复杂度
需要r个辅助队列,空间复杂度= O(r)。
2.时间复杂度
一趟分配O(n),一趟收集O(r),总共d趟分配、收集,总的时间复杂度=O(d(n+r))
3.稳定性
基数排序是稳定的。
3.基数排序的应用
1.学生年龄排序
某学校有10000学生,将学生信息按年龄递减排序
生日可拆分为三组关键字:年(1991-2005)、月(1-12)、日(1-31)
权重:年>月>日,年、月、日越大,年龄越小。
- 第一趟分配、收集(按“日"递增)
- 第二趟分配、收集(按“月”递增)
- 第三趟分配、收集(按“年”递增)
若采用基数排序,时间复杂度= O(d(n+r)),约等于 O(30000)
若采用
O
(
n
2
)
O(n^2)
O(n2)的排序,约等于
O
(
1
0
8
)
O(10^8)
O(108)
若采用
O
(
n
l
o
g
2
n
)
O(nlog_2n)
O(nlog2n)的排序,约等于O(140000)
可以看到这里采用基数排序时间复杂度会更低。
2.基数排序适合解决的问题
- ①数据元素的关键字可以方便地拆分为d组,且d较小(反例:给5个人的身份证号排序)
- ②每组关键字的取值范围不大,即r较小(反例:给中文人名排序)
- ③数据元素个数n较大(擅长:给十亿人的身份证号排序)