小白慎入!本文难度比较高,需要对红黑树有一定的了解再来看!
红黑树
红黑树是一种高级数据结构,是平衡树大家族中的一员,并且听名字就知道这个玩意不是凡物,可能你从未听过,但是你一定会为这样的数据结构感到震撼!它的思路是如此巧妙,让人不得不感叹它是一个艺术品。不仅如此,红黑树依赖它出色稳定的查找、插入、删除特性得到了广泛的运用,是一种经得起实际工业标准作业拷打的数据结构。
文章前提声明
本文不会写任何的代码,因此本文不适合那些纯粹为了CP CODE的读者,或者只是为了了解算法具体步骤的读者,同时本文难度较高,不适合没有背景知识的小白。文章都是我在学习红黑树时候的总结,看完这篇文章你就能够明白红黑树的插入删除原理甚至是设计的思想。丝毫不夸张的说,本文章在理解深度上绝对吊打99%讲红黑树的教程,但是在此之前你必须要学过二叉搜索树(BST)以及B树还有红黑树的一些基础知识。阅读完之后,如果你还想进一步获取具体完整的代码可以选择阅读算法导论或者其他文章。
红黑树与平衡树
先来全面了解红黑树和平衡树。实际上红黑树本来的名字不是红黑树,它的名字叫做对称二叉B树(记住关键词,二叉,B树),后来1978年一篇关于二色框架的论文中用了红黑两种颜色来讨论这种结构的树,后面就沿用了这个名字。那么从原来的名字就可以知道红黑树的思想来源于B树,实际上也可以认为是将一棵B树“二叉化” 并且二叉化的结果拥有和B树相同的优秀特性。那么第一个疑问就是:那为什么要用红黑树不用B树呢?——并不是不可以用,而是实现难度非常高、繁琐,二叉类的平衡树相对于具有不同类型节点的平衡树而言一个显而易见的好处在于每一个节点都具有同样的结构,而B树不行,真正的B树的节点应该是用一个有序链表进行维护的(数据结构套数据结构)。而这也反映了为啥平衡树在概念上很简单但是具体实现却很复杂。因此平衡树的“完美平衡”的定义就很关键,比如AVL树就是任意节点的左右子树高度不超过1,红黑树就是那五条法则(后面会讲)等等,不同的平衡树有着不同的平衡定义,也就导致有些平衡树看起来十分优秀但是没人用(超难实现,二阶AVL等等),而一些看起来比较“弱”的平衡树超多人用(ACM常用的Treap,Splay,为什么说“弱”,是因为这些平衡树的随机性更强,因此严格的算法分析是更加困难甚至无解的,大多数时候说的是操作均摊的期望复杂度)。尽管这些简单的平衡树损失了一些理论上的优势,但是因为放到计算机上的时候仍然要考虑计算优化以及实际的计算机物理限制,因此常数低的代码跑的还不一定比理论更优的慢,而且哪怕真的到了数据规模很大的时候,平衡树的性能也不会有非常明显的差距!(在统计学习有一个“天下没有免费的午餐”的定理,对于不同的数据和不同的操作,谁能保证AVL一定跑不过红黑树,而红黑树一定跑不过AVL,不同的平衡树具有不同特点的操作,比如Splay的区间操作,我对此印象超级深刻,不同的应用场景选择不同的平衡树才是正解!)
好的,为啥我要讲这么多和红黑树操作没有关系的东西呢?因为我想让我的读者知道红黑树为啥叫红黑树,为啥它和B树有关系,以及为啥二叉化?如果你懂了这些,你已经比那种背代码的强太多了——你学会了如何去设计数据结构!学会了如何在理论和实际性能做取舍!
红黑树和2-3-4树和2-3树
当初学红黑树的时候,无意之间接触到了两个新词:2-3树和2-3-4树。这两个东西很简单,实际上就是三阶和四阶B树。
下面就构造一下这些树的样子,这里我使用算法可视化的网站来完成,因此结果很可靠:(1,9,2,8,3,7,4,6,5,这个数据BST如果不平衡就是一坨屎)
BST(二叉搜索树):
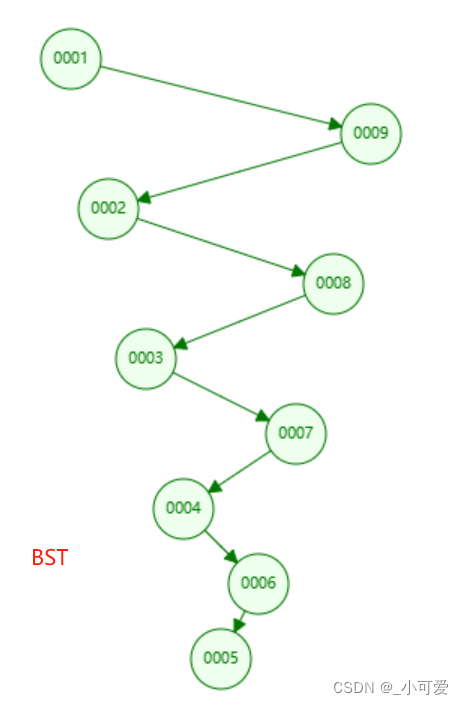
2-3树(三阶B树):
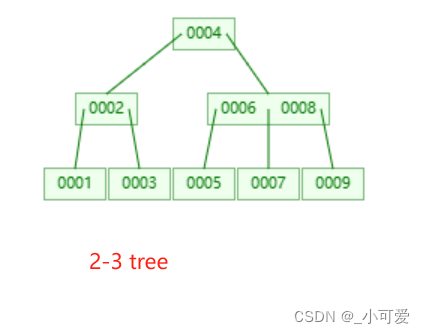
2-3-4树(四阶B树):
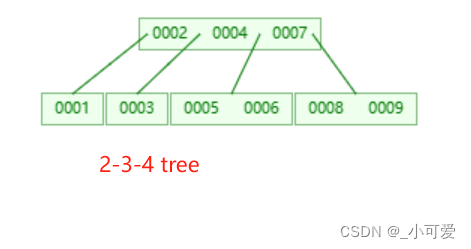
红黑树:

从上面就可以发现一个重要的事实是B树天生具有平衡的特性,本质在于B树中的每一个节点到达它可以到达的叶子节点的路径长度是相同的(分层)。这个实际很好证明,使用数学归纳的方法就可以了,我这里简单说说:假设当前B树满足这个特性,那么能够增加路径长度的操作必然是节点分裂发生上溢,此时原来的节点变为两个,上溢的节点到所有的叶子节点高度加一,路径长度相同性质仍然满足,表明上溢操作不会影响该性质。
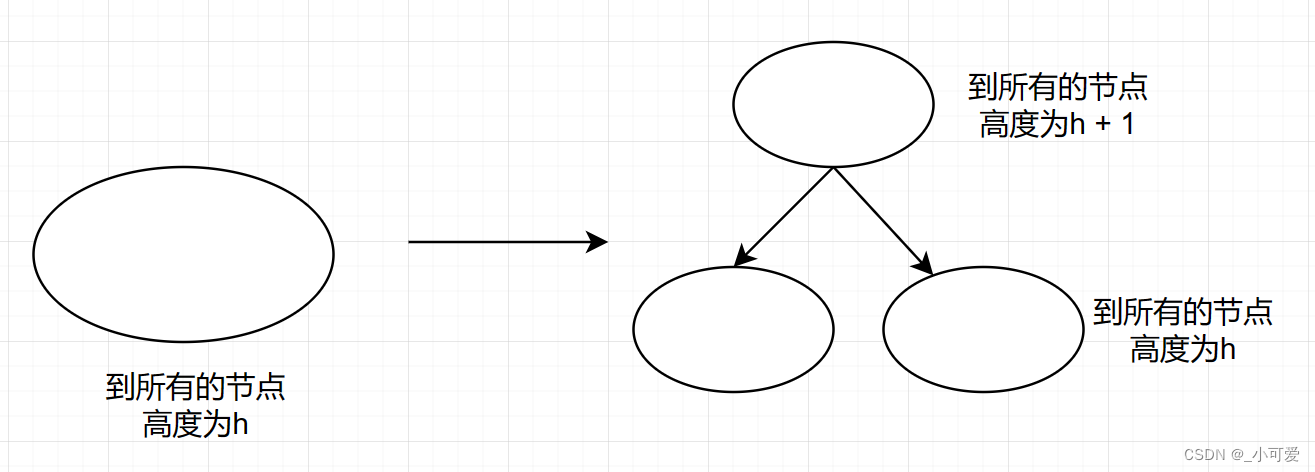
因此如果能够简单地实现这样优秀的数据结构那岂不美哉?哎,红黑树就诞生了,红黑树实际上就是一棵2-3树或者2-3-4树的二叉化形式。然而实际上,基于双色框架,我们可以将这个玩意扩展到m阶B树的二叉化,但由于2-3树和2-3-4树是属于B树中最简单的了,并且恰好避免了一些很麻烦的事情!:)后面会说。所以目前大部分红黑树的代码实现是基于2-3树或者2-3-4树的。
所以红黑树的第一个平衡原则是:红黑树上的任意一个节点到叶子结点的路径上黑色节点的个数相同。(黑色节点个数相当于B树上的距离)
如何二叉化
我们使用红边的形式规定:红边构成的连通块属于一个node。
下面是2-3树中3-node对应的二叉化的节点关系:
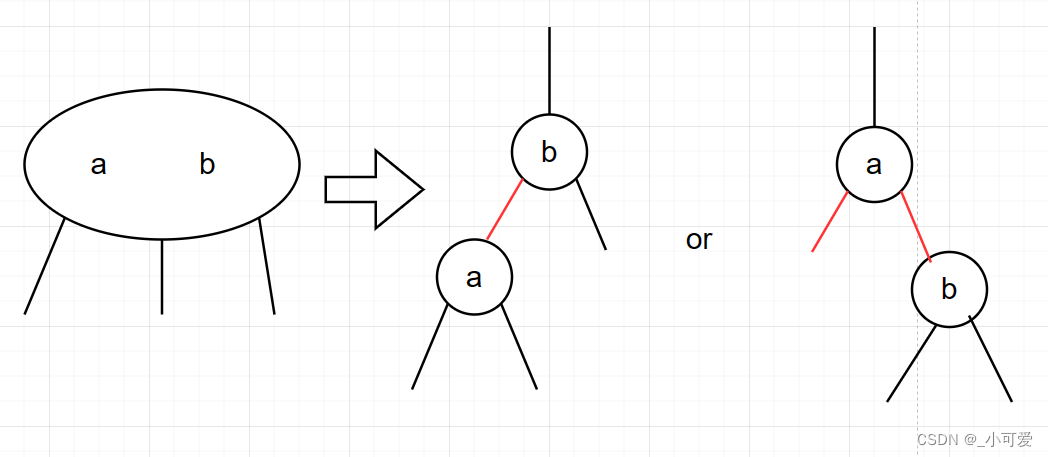
下面是2-3-4树中4-node对应的二叉化的节点关系:
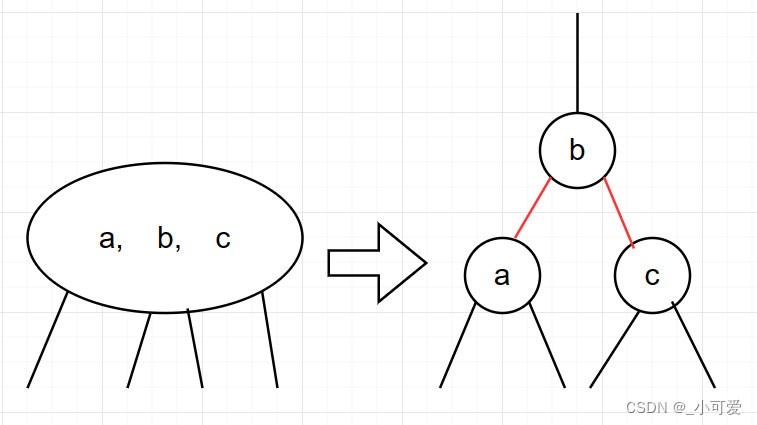
这里可能会迷惑为啥4-node是左右双边的形式而不是连续的红边形式——主要是设计的时候,我们认为这样更加平衡,论文中没有说为啥这样更好,我的观察是——也就是对于一个4-node,我们最多比较两次就可以得到结果,而如果使用连续的红边,那么最坏情况我们需要走两次次红边也就是比较三次!整体上树的高度是更低的!因此我们认为这样更好,当然也可以不这么做!只不过可能会得到一些很糟糕的结果和更加难实现的代码!因为这样的4-node形式上是不统一的,如果我们允许连续的红边,那么4-node具有三种形式,所以对应的代码操作非常繁琐!
所以我们可以得到红黑树的第二条重要的平衡原则(基于2-3-4树等价):从一个节点出发不可能连续多次经过红边。
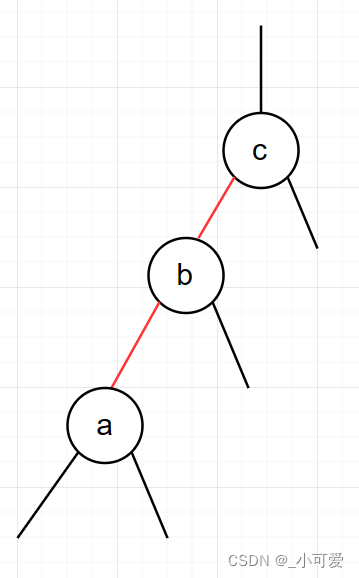
为了更加通用以及方便(2-3树的讨论可以看红色的那本《算法》,但是2-3-4树的算法是更加通用的),下面我都是讨论2-3-4树等价的红黑树并且省略NIL节点。
所以现在我们可以上面的那个红黑树转换为下面的2-3-4树形式:
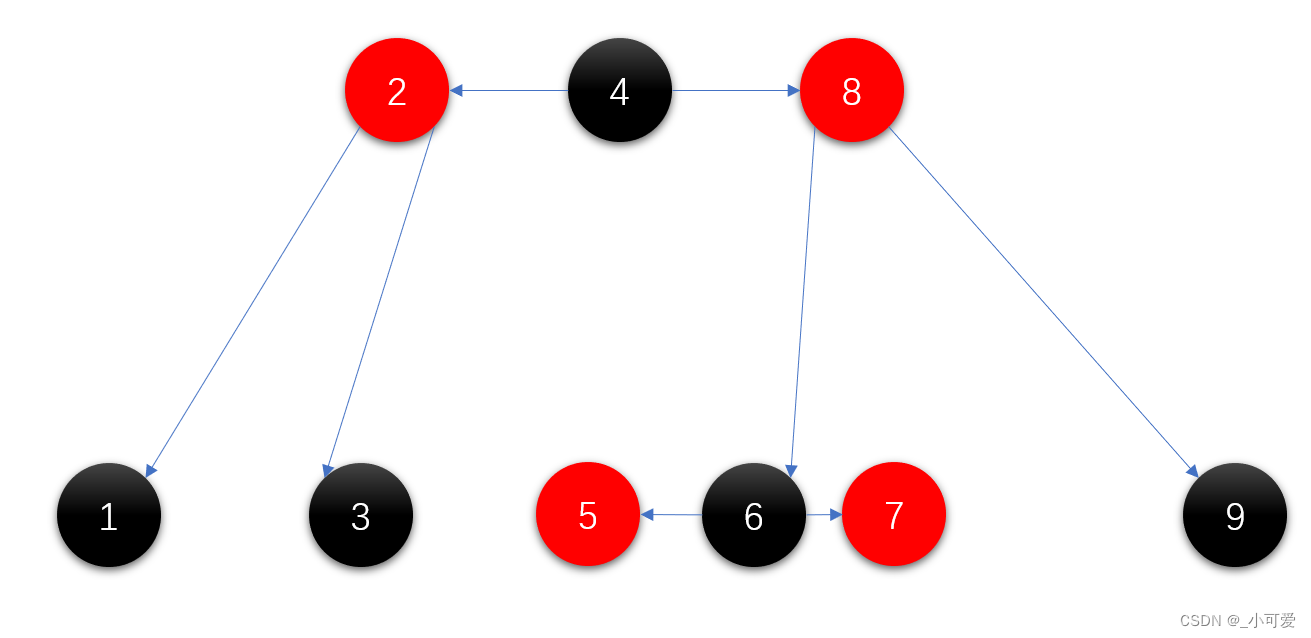
其中的2,4,8构成了一个4-node,5,6,7构成了一个4-node。
插入操作等价性的讨论1(bottom-up method)
在讨论操作等价性的时候,可以从两方面的逻辑来思考这个操作到底是对的还是错误的:平衡原则和2-3-4树对应操作。首先如果我们从平衡原则来考虑等价,也就说我们的操作能够实时维护这五条性质,也就相当于保证了红黑树的平衡。另一方面,我更加推荐的是从2-3-4树的操作来思考操作的等价性,也就是从设计者的角度出发来理解红黑树的维护操作。具体的例子请接着往下阅读。
上面我们讨论了关于红黑树本质上是2-3-4树的二叉化形式,那么对于2-3-4树的操作,我们又该如何进行等价?实际上这非常巧妙,首先我们明白了一个关键的事实:插入的关键操作在于上溢。
那么我们还是从2-3-4树出发来考虑这样一个事实:因为我们每一次找到插入的位置的时候都是想要合并到找到的节点,所以我们规定每一次加入的都是一个红颜色点或者说将插入的点和父亲连接一条红边。那么唯一可能发生上溢的情况就是插入的节点恰好是一个4-node,假设你从未学习过红黑树,你该如何设计这样一个上溢的过程呢?(2-3-4树对应操作角度思考)
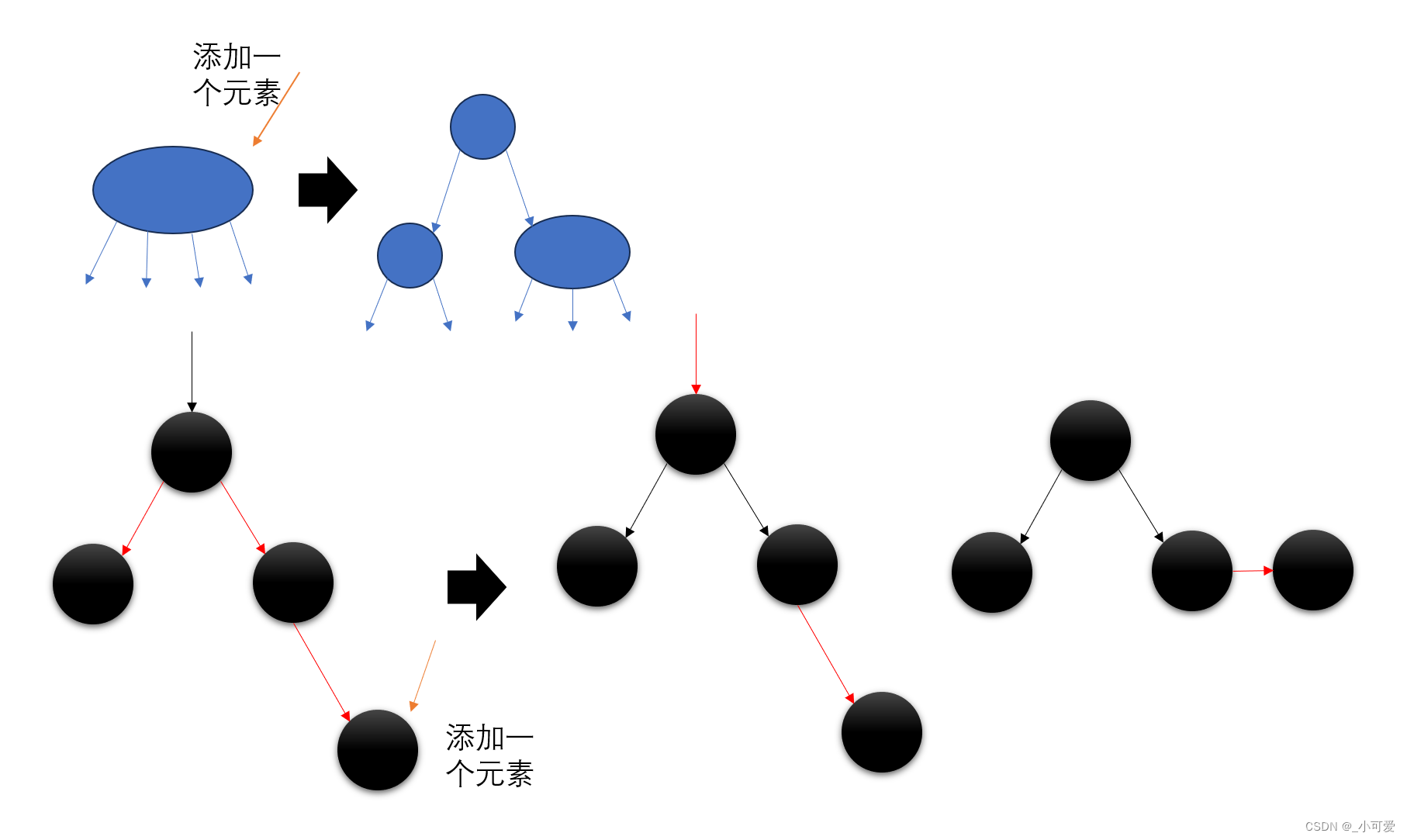
实际上很简单,我们只需要做的就是颜色反转!——将边的颜色修改一下,我们把内部的中间节点弹出去相当于让它和它的父亲合并,然后原本的节点一分为二,所以原来的两条红边变为黑色。操作完之后我们也可以检查有没有违背我们之前说的两条平衡原则(平衡原则角度思考),仔细检查一下就可以知道是没有的,因此该操作是正确的。
然而仅仅有这个操作我们还无法很好地维护其中的第二个平衡原则:不会连续经过两条红色的边。所以我们需要一些操作来维护这个性质(平衡原则角度思考)。
更加深入的理解, 在这里我们很容易发现一个事实,就是对于一个2-3-4树的节点而言,比如4-node,它里面的具体结构是不确定的我们只知道了它有四个孩子和三个键值,但是对于红黑树而言是可以看得到的,那么我想说的是,在红黑树里面它这个节点的结构是一棵简单的平衡BST,说白了我们要维护红边连通的子树是一棵平衡的BST。(这里留下我的一个idea:B树的节点实际上可以认为是一个数据结构,那么它可以是有序链表,为啥就不能是平衡树呢?所以红黑树本质上是把这个数据结构变为了平衡BST融到了原来的B树里面?如果是这样的话,我们可以用这种双色框架实现任意的平衡树结构,将实现复杂的两层的树变为一层,比如说m阶的B树里面的节点对应的是一个高度不超过lgm+1的简单BST,甚至更加大胆,对于具有内部结构的节点的数据结构我们能不能用类似的方法将其扁平化?)
对于一个最多只有三个点的简单平衡BST,那么不平衡的只有四种情况(LL, RR, LR, RL):
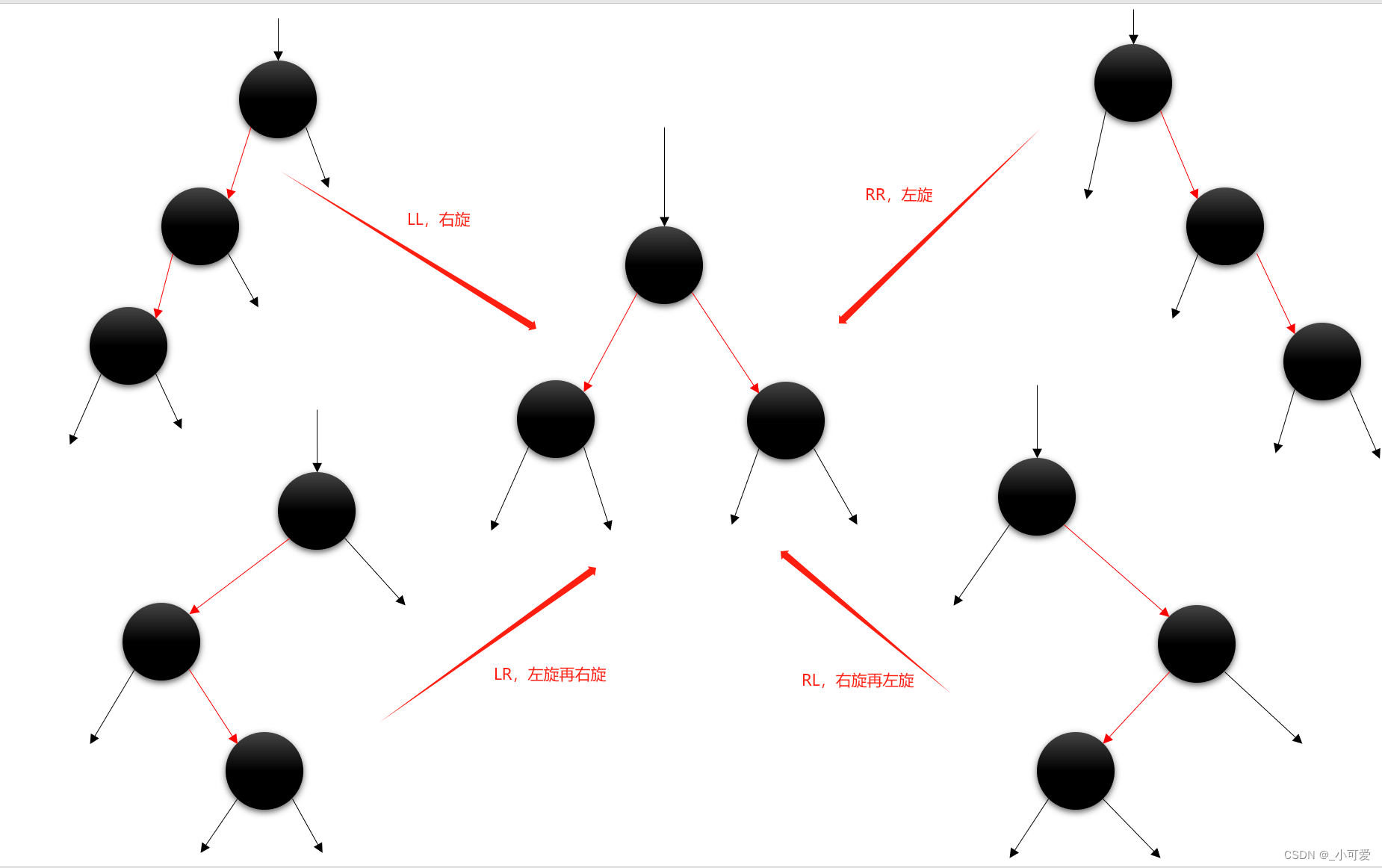
操作完之后我们再去检查一下有没有违背第一条平衡原则,可以发现到达叶子的每一条路径的黑色边数量还是不变的,因此该旋转操作并不会影响第一条平衡原则。
所以整个插入的流程就是向下搜索找到插入的位置,然后不断向上回溯,判断是否会发生上溢,是否需要使用旋转去完成平衡。
插入操作等价性的讨论2(top-down method)
论文里面提出了一个简单的top-down插入算法,它可以做到一次性往下插入而不需要回溯调节平衡。它的思想也很简单,就是在插入之前就已经把路径调节好,这样的话看做是提前的“balance”,到最后面的时候直接插入就可以了。
具体的做法可以看看下面的图片:

可以证明按照这样的插入方法进行插入,到达最后的一个节点时必定不会发生上溢操作。
证明:假设在最后插入的时候发生了溢出,那么最后一个节点必然是属于4-node,由于我们的操作表明在遇到4-node将发生主动分裂,所以该节点不可能是4-node,矛盾。假设不成立。
而其中的平衡调整也是自上而下的,因为可以发现平衡操作只会发生在产生4-node的时候,那么唯二可能的情况就是:上溢导致了父亲节点变为4-node,最后的插入产生了一个4-node。对于第一种情况,由于我们是从上往下调整,所以对于当前分裂的4-node,它只会可能影响到它的父亲,所以对父亲做一次平衡即可。对于第二种情况,我们只需要调整该4-node即可。因此该平衡操作整个流程可以自上而下完成的。
下面展示了使用这个方法插入 1,2,3,4,5
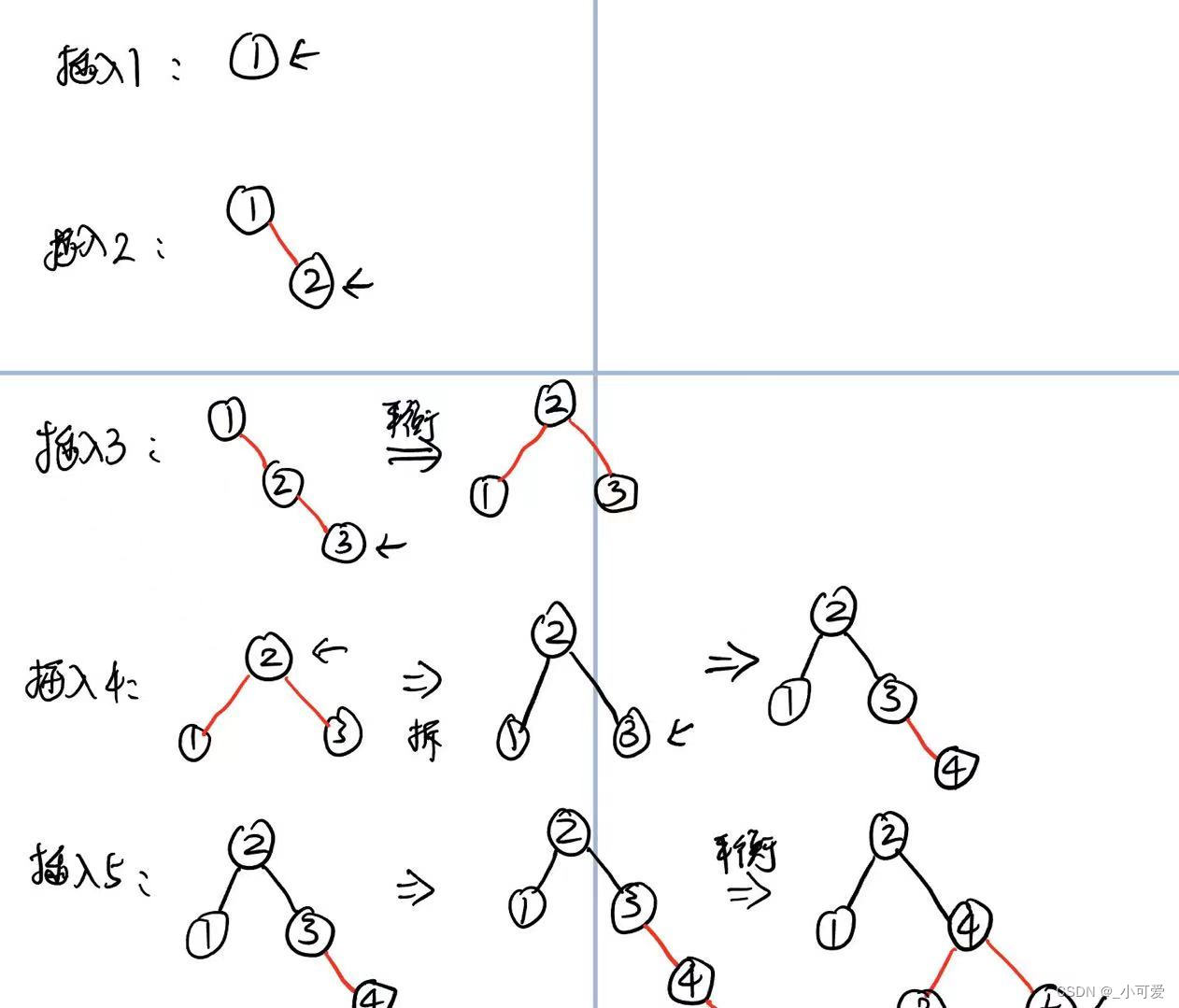
个人认为插入算法无论是哪个其实都还算是比较好理解的,本质上就是为了维持平衡原则,基于这个出发点就很好理解。
删除操作等价讨论1(bottom-up method)
通常我们认为平衡树的删除操作难度要大于插入。对于2-3-4树来说,我们如果想要使用自底向上的方法去删除,那么最好的选择是操作它的前驱或者后继,这样子的话我们就可以将所有的删除转变为叶子节点的删除。(实际上这对于自上而下的删除方法来说也是更好的选择,因为这样可以避免对左右子树的讨论)
我们先看2-3-4树的删除操作(2-3-4树操作角度思考),然后我们再视图将这样的操作等价到红黑树里面。
(讲个笑话,B树的删除是一场大型的家产继承活动!)
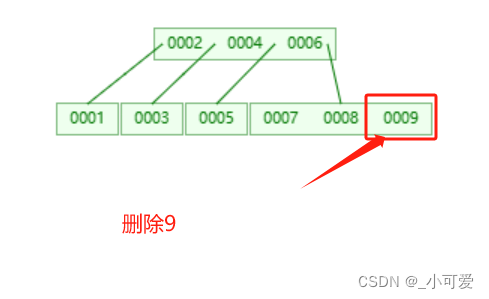
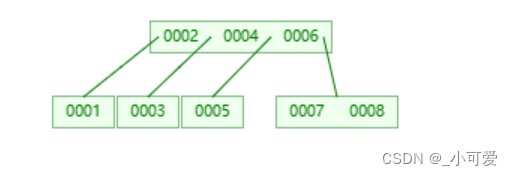
可以发现一点是我们删除叶子上面任意一个3-node, 4-node都不会对树的平衡发生任何影响!本质原因就是在于它不会影响树的结构,删了一个9但是7和8仍然是一个node。这时候我们再去删除5,就会发现一个树的结构变了!——4和6中间没有了孩子,这是不合法的,这个时候根据2-3-4树的方法就是——把父亲拉下来,然后检查自己的儿子有没有可以继承家产的,如果有的话就将它拉上来继承家产,如果没有那么就一家团聚。
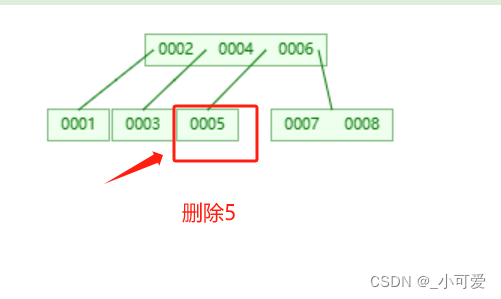
把父亲6拉下来,发现儿子7或者8可以继承家业,这里选择7,那么7上去,6下来。
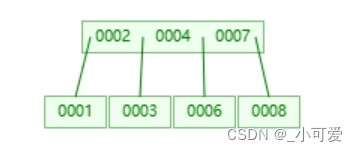
现在我们要继续删除1,
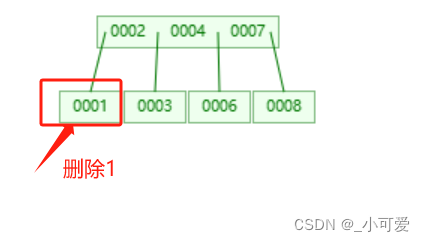
那么1的父亲2就要下来,但是发现只有一个儿子3,没有儿子能够继承家业,所以一家团聚,2和3合并。
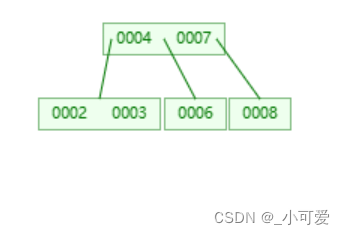
讨论了2-3-4树的删除之后我们就要想该如何去等价这样的操作呢?首先最显然的一点是如果删除的点属于一个3-node或者4-node,那么就等价于2-3-4树中删除一个3-node,4-node叶子的情况,此时直接删除不用做任何处理。因此最困难的地方在于删除一个叶子是一个2-node的情况,此时要做的就是分类讨论。
同样的我们还是按照2-3-4树等价操作出发,首先看一下兄弟有没有能够继承家产的,如果有的话那么兄弟一定是一个3-node或者4-node。
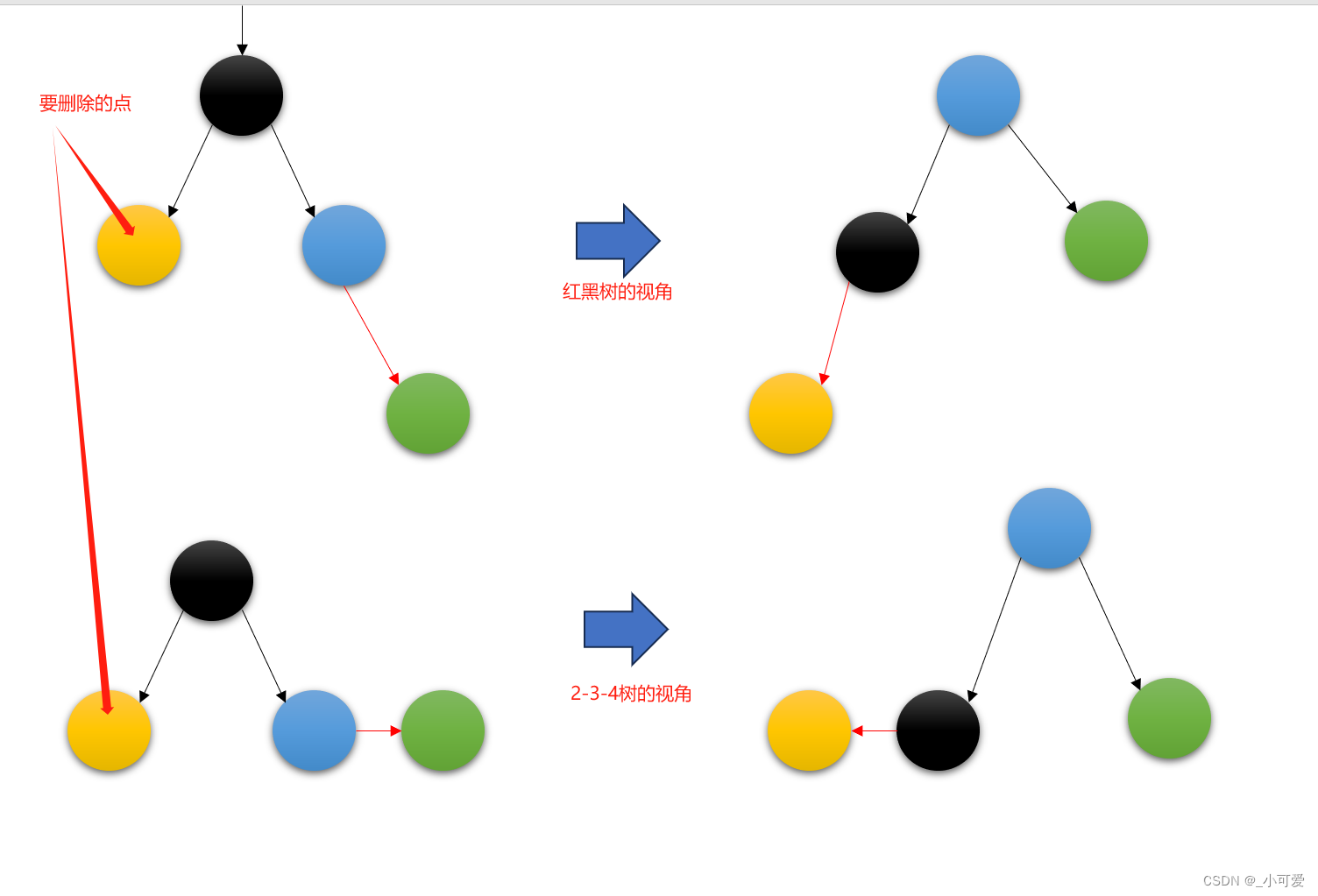
基于上面的操作之后我们就可以直接将黄色的点删除掉。深入思考操作的本质,我们只是通过了左旋和右旋来调整父与子之间的关系罢了。因此对应的兄弟如果在右边,那么分别有3种情况:兄弟有一个红色的右儿子(左旋),兄弟有一个红色的左儿子(右旋+左旋),兄弟有两个红色的儿子(任选一个),我们分别做对应的旋转即可!
那么如果兄弟儿子没有能够继承家产的怎么办?这个时候我们将父亲(黑色)拉下来和它的儿子(浅蓝色)进行合并,这个时候就相当于递归的删除了父亲,我们就要处理父亲的位置了,看一下有没有叔叔节点(深蓝色)可以替代父亲的位置,如果有的话,那么叔叔就可以替代父亲的位置继承家产,如果没有那么祖父(棕色)就必须下来和叔叔节点合并!相当于递归向上的过程,直到可以继承家产的人出现!
可以看看下面的操作示意图(删除黄色节点):
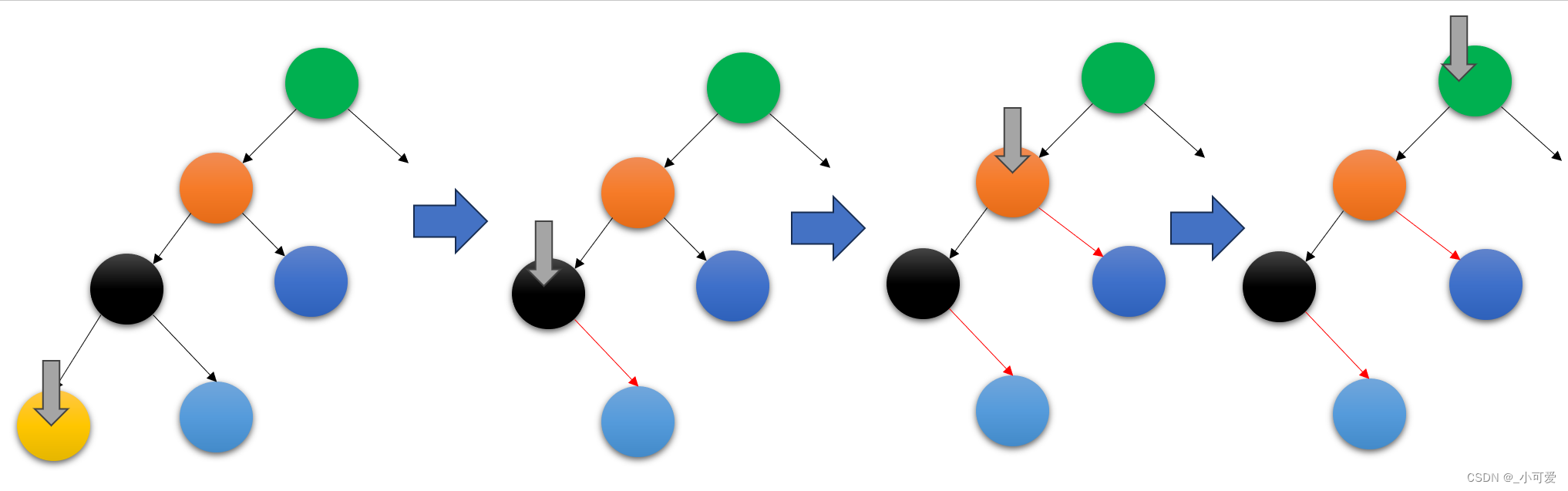
下面不同的角度看这个删除的过程:
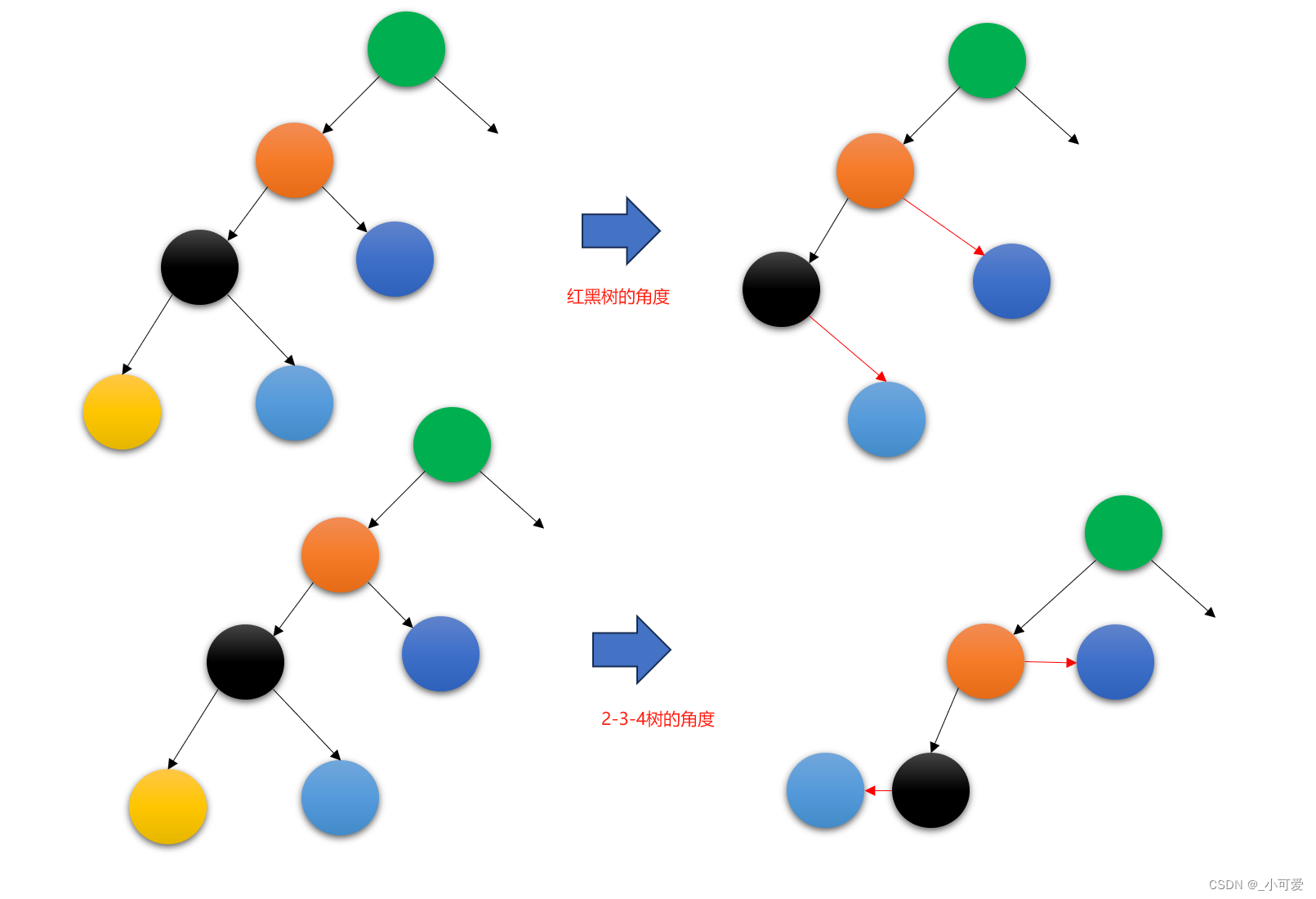
上面的过程中,没删除前的红黑树是部分结构,所以你看到的可能不满足第一条平衡原则(黑色边数相等),但这对我们的删除操作没影响,只要我们保证删除后还是能够和没删除前一样经过相同的黑色边数即可。
仔细思考一下这个过程的本质:无非就是把父亲拉下来和儿子合并然后递归处理删除的父亲这个位置。 在2-3-4树里面这就对应多层的下溢过程,并且操作的过程十分简单,我们合并下溢的操作只需要将父亲到儿子的边标记为红色即可。很多人不理解这个地方,我觉得可能是没有理解这是一个递归的过程和2-3-4树的下溢合并操作。我们刚才讲了红黑树插入的时候是向上溢出,本质上是因为了一个节点满了导致不得不分裂,父亲被分裂开,会继续向上和祖父合并。而删除也是如此,本质就是一个节点个数太少了不得不向下合并,儿子消失了,父亲不得不去替代他,于是祖父会继续向下合并处理父亲的位置。
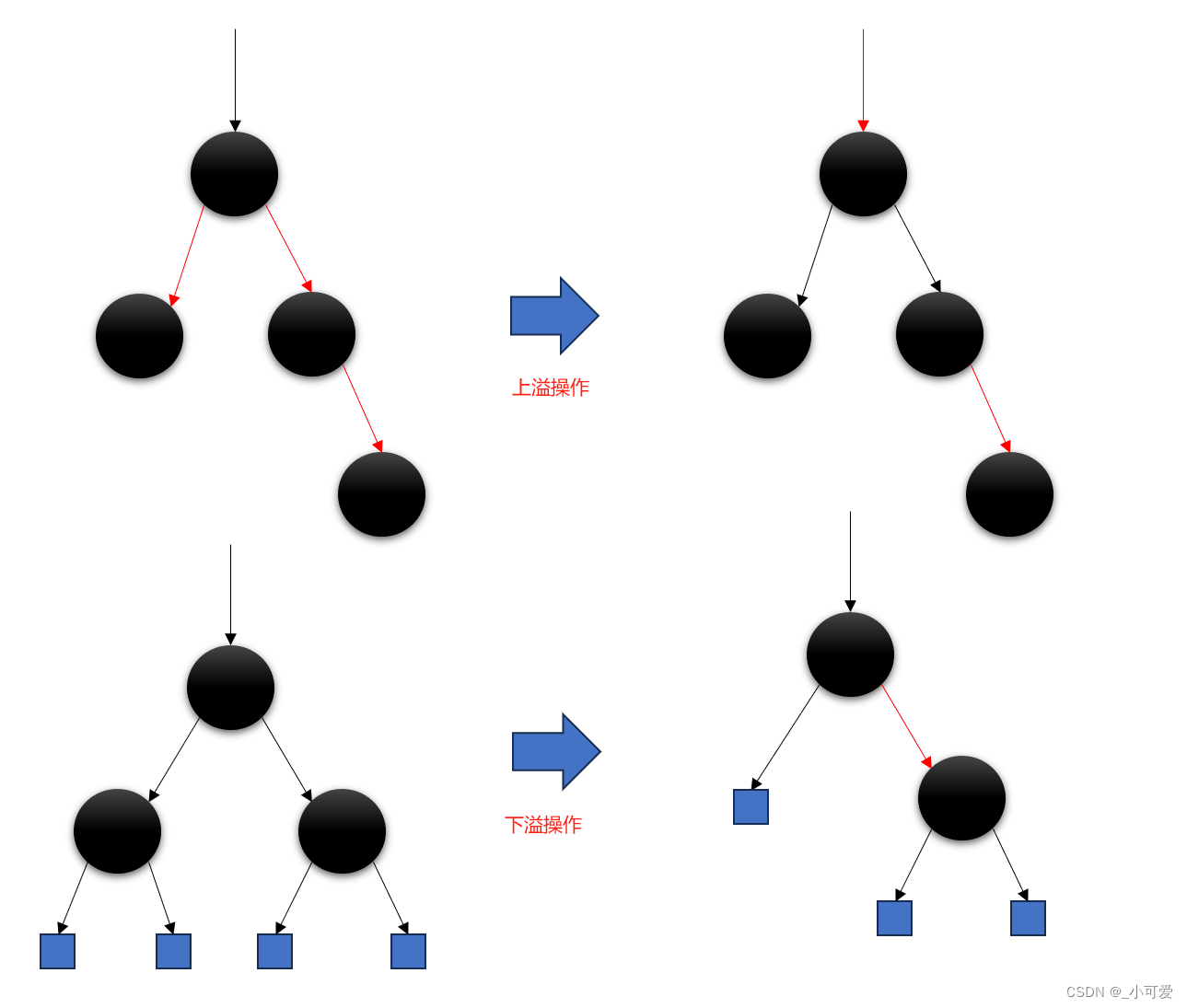
这个过程非常抽象,但是我觉得已经讲的很明白了——就是不断的下溢操作,实现也只需要做恰当的颜色反转即可实现!当然,如果是别的文章现在就结束了,但是我明白你看了上面的递归删除可能还是一头雾水,所以我将介绍从自顶向上的角度看待刚才的递归删除!
删除操作等价讨论2(top-down method)
我们假设上面例子中的曾祖父(绿色)是一个红色节点。
那么实际上一开始是这样子的:

经过上面的递归删除后,我们可以得到:
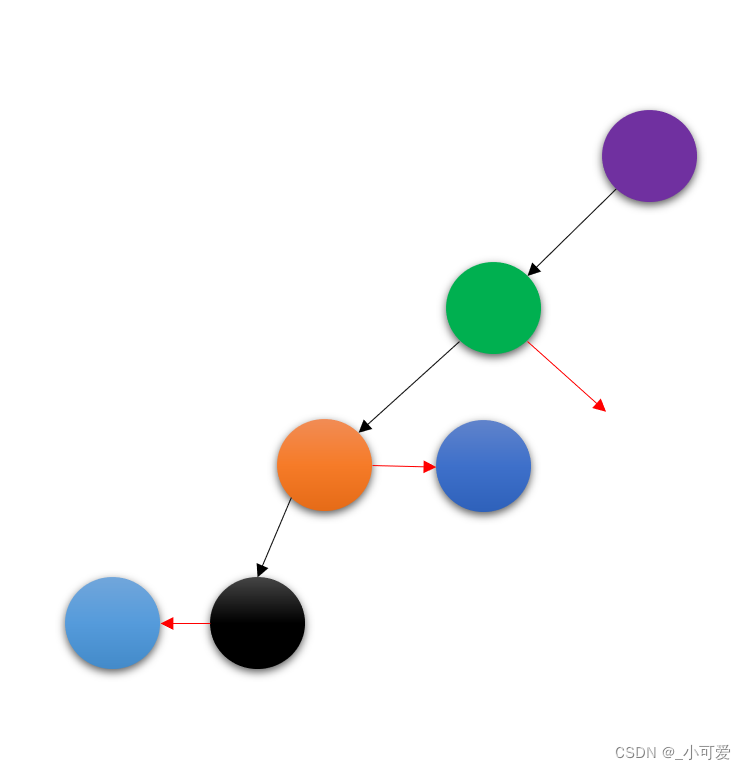
其实实际上我们刚才讲过了一个自定向下插入的时候是主动将4-node(因为插入就会上溢的节点)进行分裂上溢,那么删除的时候我们做相反的事情,我们主动将3-node或者4-node拆解进行下溢合并。
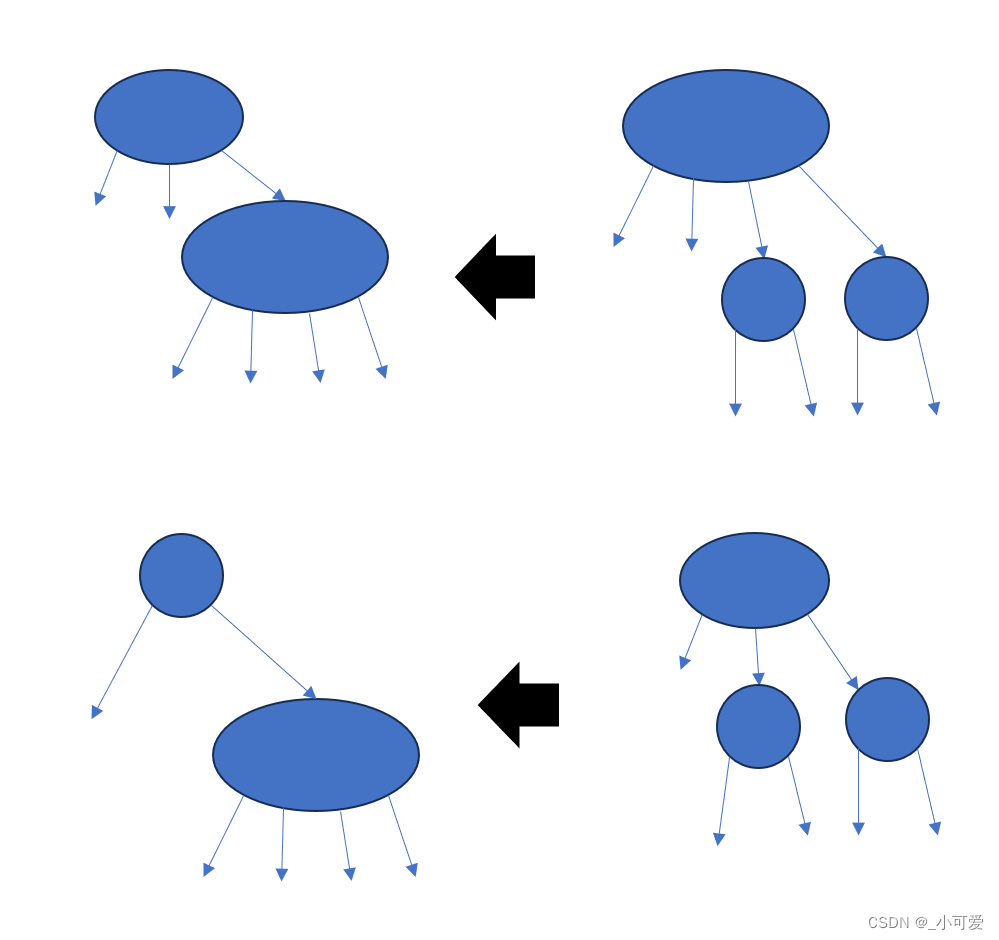
这样子的话我们在最后删除的时候一定可以将该需要删除的点变为红色,所以无须考虑黑色节点的情况。
下面是不同种类的主动向下溢出的过程示例(具体的不同情况可以自己分析一下):
父亲主动分裂下溢:
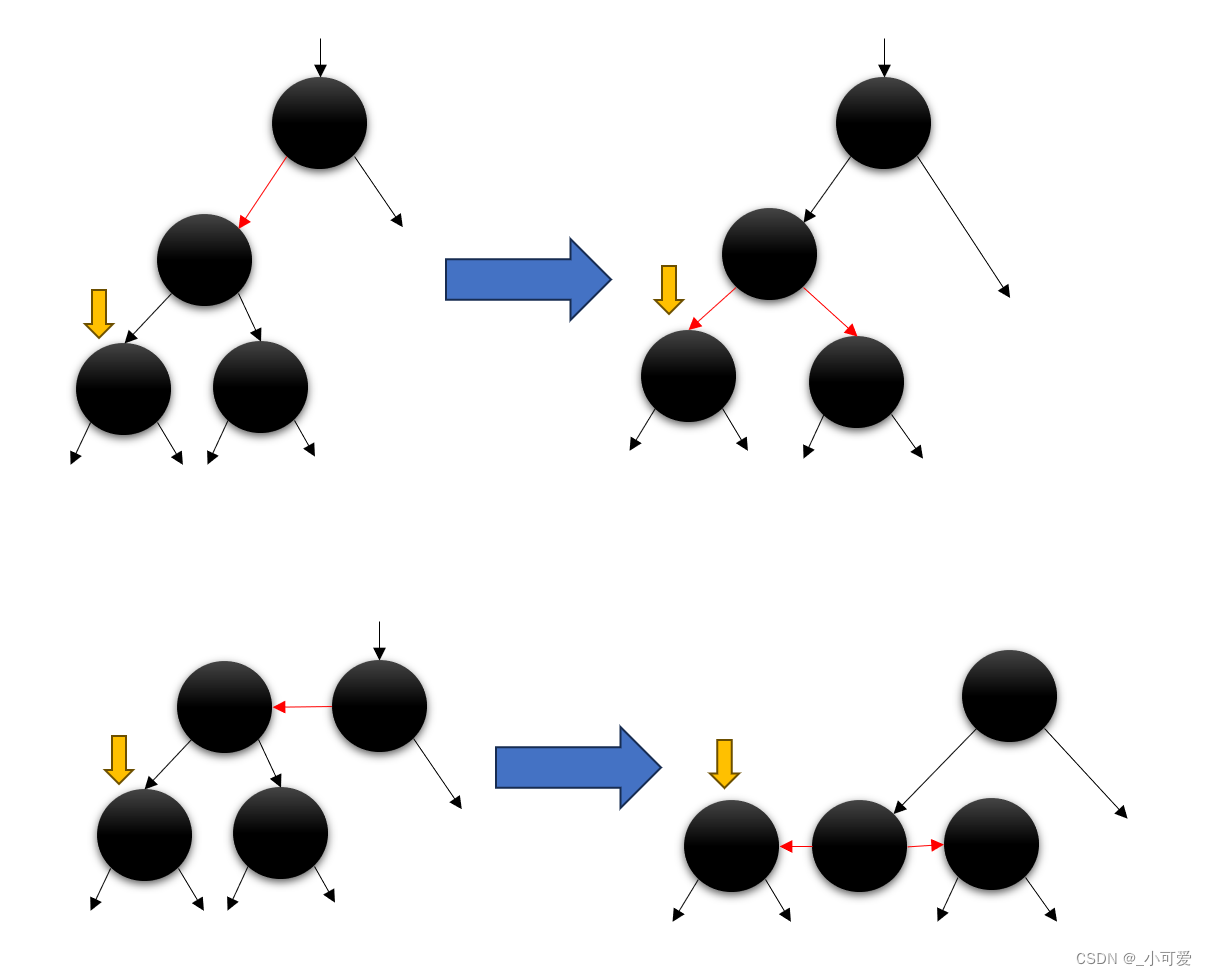
兄弟主动分裂下溢:
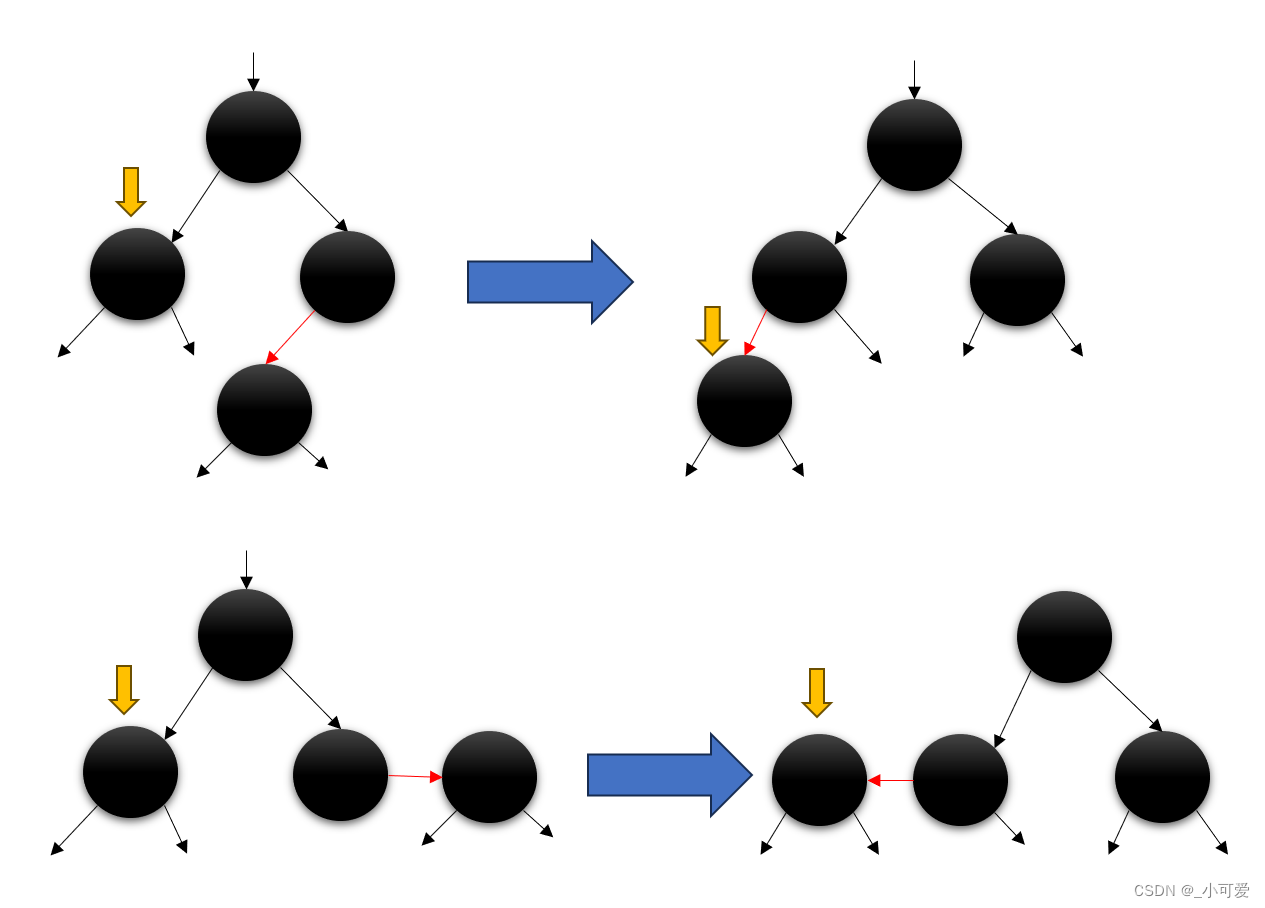
可以观察到父亲主动分裂下溢和兄弟主动分裂下溢的过程刚好对应了上面bottom-up method里面的一些方法,比如说父亲主动分裂下溢就相当于父亲下溢合并,而兄弟主动分裂下溢就相当于兄弟节点继承家产。
那么对应于一开始的那个例子,删除黄色节点的过程就会变为这个样子:
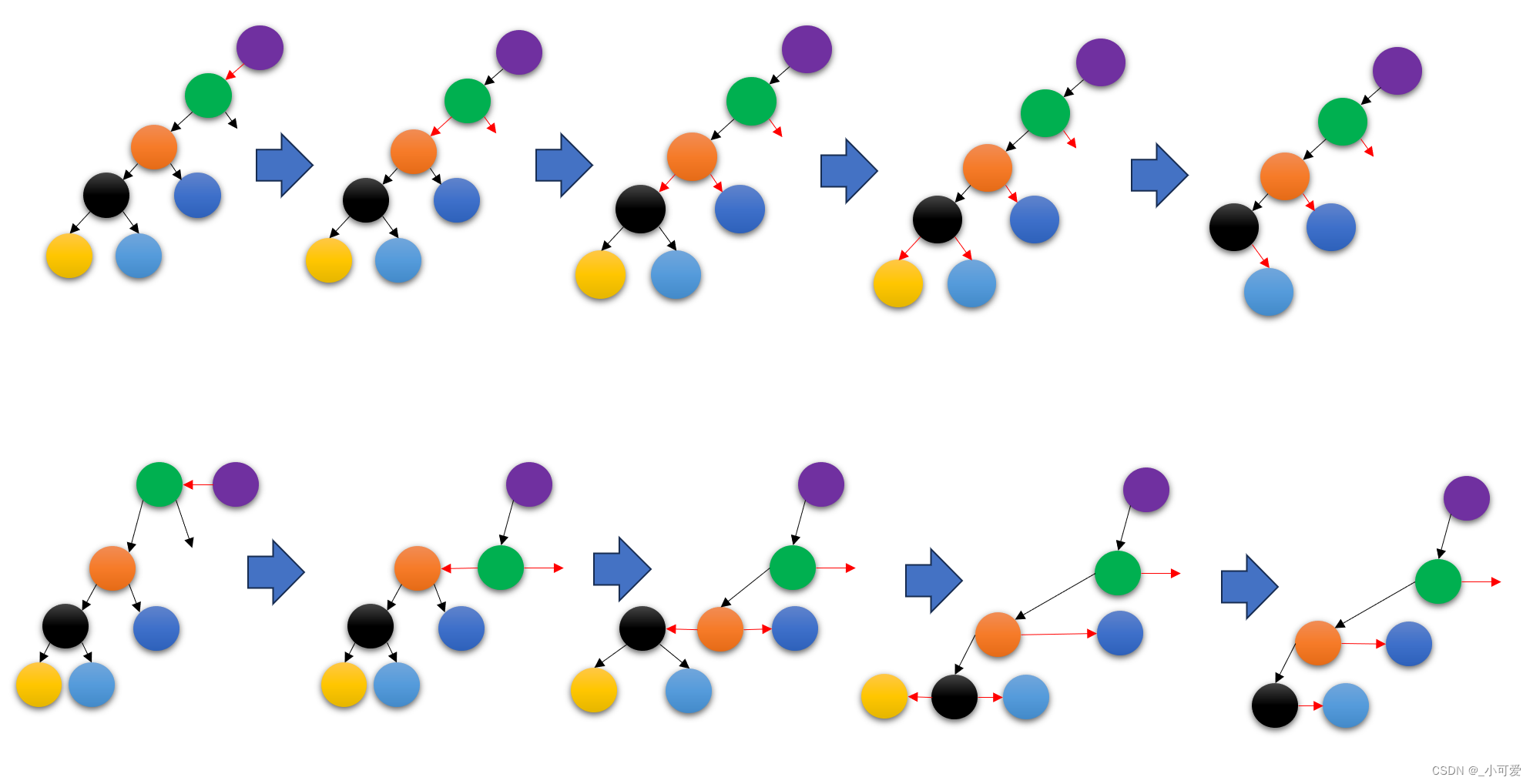
最后的结果是一样的!实际上我们还可以发现一个事实:自顶向下的方法实际上就是把红色边往下push,然后递归的删除方法实际上就是相当于往下pull,一个拉一个推。
题外话
一个问题:自己,儿子,父亲,祖父都为黑节点,上面的这种情况真的可能出现吗?问题来源于我在构造数据的过程中,我发现一个这样的情况非常难以构造!如果直接使用正常的插入我断定是不可能产生这样的红黑树的。但是问题是它并没有违反我们定义的红黑树的五个原则。除此之外,这也引发其他的问题:是否对于不违背性质的红黑树我们总能用正常的插入删除构造出来?
下面是我能够构造的最黑的红黑树:(顺序插入1,2,3,4,5,6,7,8,9,10,然后删除10,9,7)
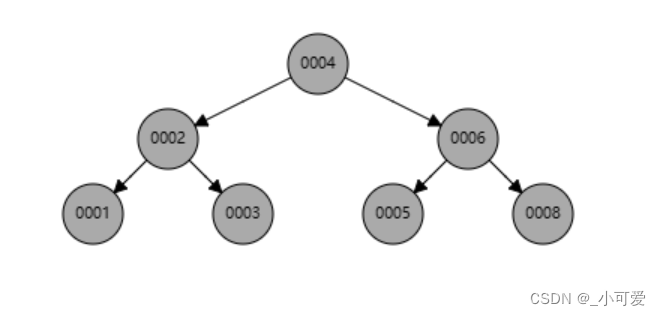
我几乎找不到自己,父亲,祖父,曾祖父都为黑色并且只有黑色儿子的情况。