触发器
D
D锁存器就是在有时钟信号时，D信号是啥，Q就是啥，并且在时钟信号消失时，锁存住消失前一刻的信号状态
主从D锁存器中，D信号是主锁存器的输入信号，主锁存器的信号是从锁存器的输入信号
用D实现的电路，大体思路就是让其他信号对现有的Q和Q非信号完成一次选择，或者进行一些处理，最后一定要把各种处理完的信号综合为一个信号，作为D的输入信号（D），因为D锁存器只接收一个信号
T
T锁存器，就是在有是信号且有时钟信号时，反转一次，要想反转一次，就是取个反，即保留Q和Q非的Q非信号，并让Q非信号对Q进行赋值，就完成了一次反转，至于Q和Q非是什么，不用管，只要保留选择出Q非信号即可
T锁存器的信号触发必须为边沿敏感，不然如果电平敏感，就会在有T信号和时钟信号时一直反转
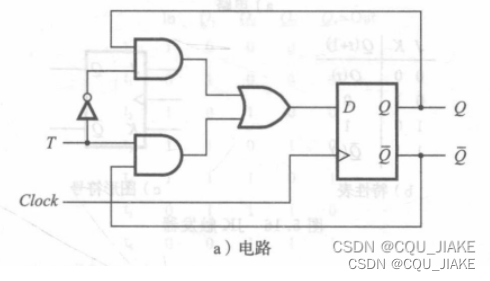
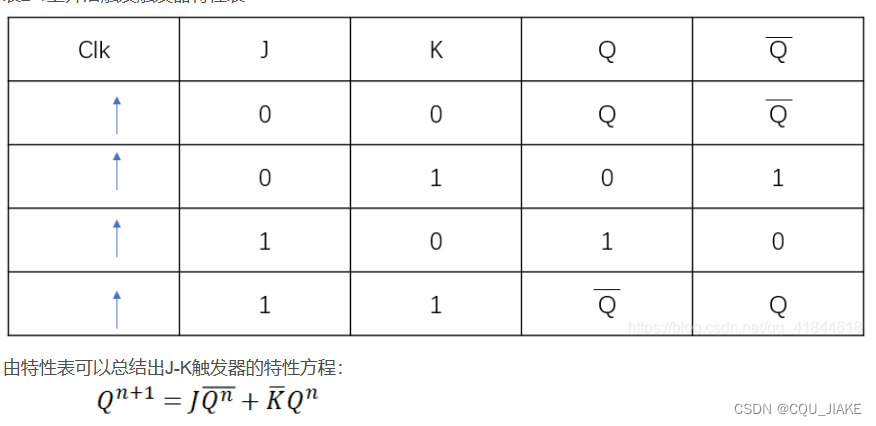
J-K
右侧还是D边沿，左侧是J-K选择方式，就是输入两个信号J,K对Q和Q非完成一次选择，然后再通过或门完成一次信号合并，作为下个时刻的Q信号
当J为1时，选择Q非信号；当K为0时，选择Q信号
没有选择时，通过与门输出0信号。
都不选择时，都输出0信号，综合为0信号，则Q被强制赋值为0
都选择时，输出Q和Q非，则或完后是1，则Q被强制赋值为1
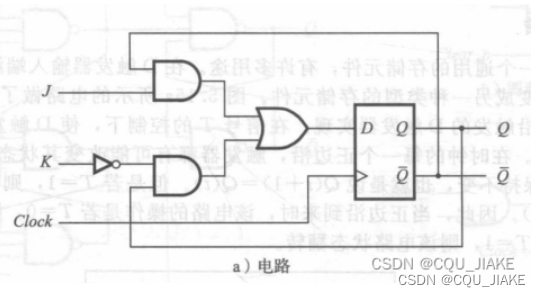
J-K触发器是选择原信号后进行处理与强制赋值两种方式的综合，有选择行为时，就是对选择的信号进行处理，不然就是强制赋值。
如果想要保存电路状态，就选择Q，即让K信号选择Q，J信号不选择Q非去实现
如果想要反转，就选择Q非，让J信号选择Q非，K不选择Q实现
如果不知道电路状态了，恢复初始状态，就都不选，那么D信号就是0，即次态Q为0
想强制Q为1，就都选，或完就是1，那么次态Q就是1
R-S
R-S大体也是，选择保存与强制赋值，但是RS不基于D锁存器进行对Q的状态转化，而是通过或非门的强制赋值实现，R信号选择赋值的是Q，S信号选择赋值的是Q非
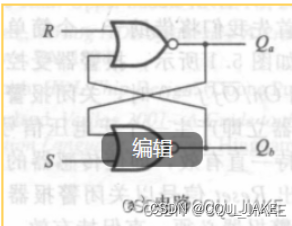
所谓选择，通过或非门，不是与门，与非门，那就是要让R,S信号对其无影响，那就是R,S为0时，R为0就算是完成了一次对Q非的选择保留，S为0就是完成了一次对Q的保留选择，但这种选择都是不会改变原状态的，R-S要想改变原状态，就是要通过不保留的选择，基于或非的性质去进行强制赋值，从而完成对状态的改变
与其说选择的是是否保留，说选择的是否强制赋值为0更贴切
信号为1时，是对路上对应信号的强制赋值（赋值为0）；
信号为0时，是选择不进行强制赋值，但保留反转的功能
在一个选择赋值时，另一个必须选择不赋值，保留反转，才能保持电路功能
都选择不赋值，保留反转时，就是存储功能，存储当前电路状态（由于非门，电路正常状态为一正一反，即不同的状态）
如果两个都选择赋值，那么都可以在有信号时，使两信号为0,但一旦信号消失，就会保存这相同的状态，但由于非门，就会不断反转
通过反转来实现就是，每次选择完后，都要通过一次非门，即反转一次，这就要求每个次态信号的电线前，选择的是这个次态信号的非信号，即如果要Q，那就要Q非，即R与Q对应，但R是选择Q非信号；S与Q非对应，但是S是选择Q信号
R为是否选择对Q强制赋值0，S为是否选择对Q非强制赋值为0，如果选择，就让信号为1，
换一种说法，是选择是否让路上对应信号的非信号为1，即如果R为1，S为0，分析是R选择对Q强制赋值为0，S不选择对Q强制赋值（即选择保留），通过R路的或非门后就是Q为0
即R为1，则Q非为1；S为1，则Q为1；
如果R-S都为0，则都不选择强制赋值
如果R选择了Q非信号，那么过非门后就是Q信号，即保持原状态
如果S选择了Q信号，那么过非门后就是Q非信号，保持原状态
如果想要保留原状态，就让R-S都选择保留原状态，那么就可以
但是要想改变原状态，就需要事先直到下个状态是什么信号，然后去赋给相应的值，即不能通过原信号来完成，
如果知道下个状态Q是0,那么就让R为1（选择强制赋值为0），或非完就是0，即Q为0
如果知道下个状态Q是1，那么就让S为1，或非完就是0，即Q非为1，再传给R的那条路，经过反转，Q就是0
（需要保证一个强制赋值时，另一个必须选择不赋值，只保留反转功能，才能保证在赋值完后的信号可以通过反转，辅助实现对整个电路状态的改变，即先赋值，后反转，保持电路正确稳定性的一个过程，即强制赋值的话，一次只能赋值一个，只能有一个信号）
或非门，包装了两个功能，一个是或，一个是非，发挥或功能时，就是要有信号1，进行强制赋值；不发挥时，就是信号0，保留非功能，即反转，保存电路状态
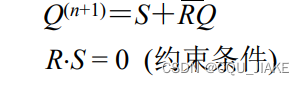
如果R为1，那就是Q被赋值为0，要S为0。即把后面整没，那就是要赋值为0
如果S为1，则R为0，Q被赋值为1。后面有没有，因为是或，所以次态都是1
如果R,S为0，则存储原状态。即直接次态等于现态
总结一下就是，J-K是基于现有状态，从中完成对下个次态的选择（通过作为D信号与D触发器实现）；R-S是基于是否选择对信号进行强制赋值（或非门，1反转强制赋值为0），来实现对电路状态的保存与改变。
锁存器之间转化
J-K与R-S区别
在上文
T与J-K
j-k是选择Q与Q非作为下个状态（因为就俩状态，要么0，要么1，要么相同，要么不同）
（要不同就是要翻转，要相同就是保持不变，锁存）
T就是选择是相同还是不相同，Q是选择哪个是（实际也就是在选择哪个作为次态，选Q就是保持不变，选Q非就是变，反转）
所以，按J-K的思路就是，如果要反转，就该是J信号，也即T信号；如果保持，就是K非信号，即T非信号
可能差别就是J-K允许接收两个输入信号，T只接收一个信号
J-K与R-S
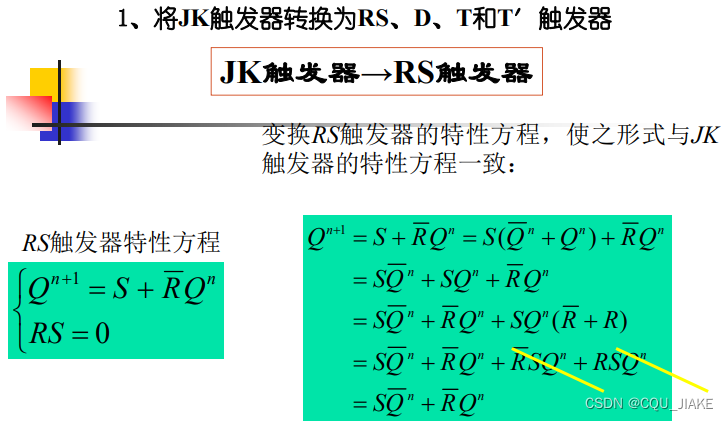
后面那个能消掉是因为RS=0,前面那个能消掉是因为前项有R非Q，根据吸收律，可以被吸收掉
S强制赋值为1，R强制赋值为0，
如果要次态为1，可以是赋值1得到，也可以是保持得到
按这个思路，如果需要赋值，那就是要改变、反转，那就说明现态是0，即Q非为1，那么此时就需要反转（强制赋值）,则S为1
如果要保持，那就是现态为1，就不需要反转（强制赋值），两个赋值信号（R-S）均为0，则次态=现态
如果要次态为0，同样思路，可以是赋值得到，也可以是保持得到
保持依旧是，都为0，则次态=现态
赋值的话，就要Q为1，则Q非为0，那么要让次态为0，则右项均为0，Q非为0，怎么与都是0，Q为1，则R非为0，即R为1
从J-K思路，是基于现态去确定次态，看次态怎么得，有哪些方式
从R-S思路就是不管现态是什么，只需要知道次态是什么
状态机大复盘
分析电路
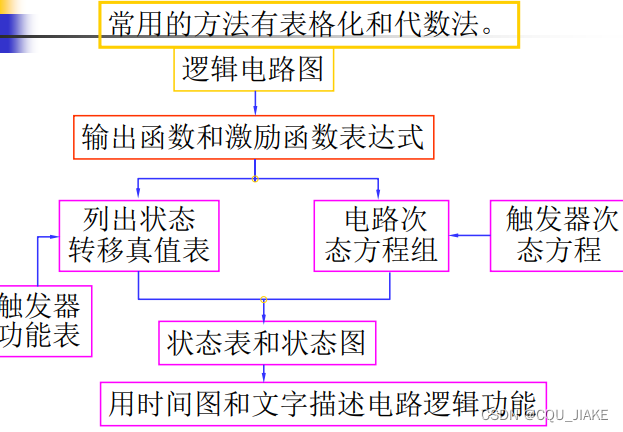
eg1
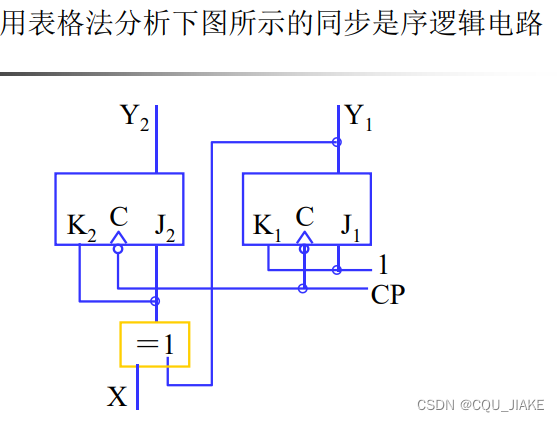
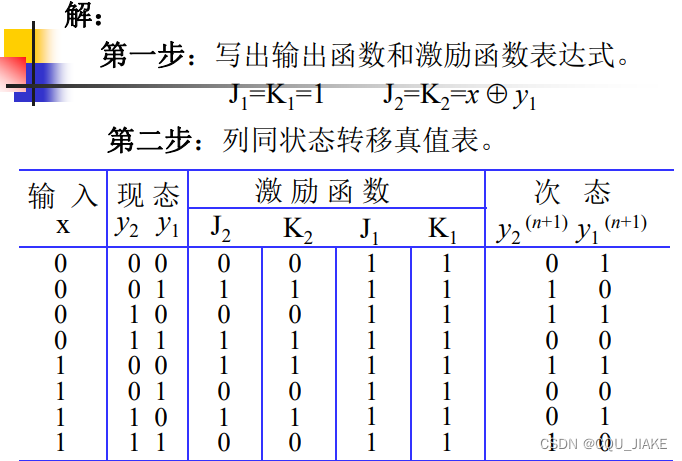
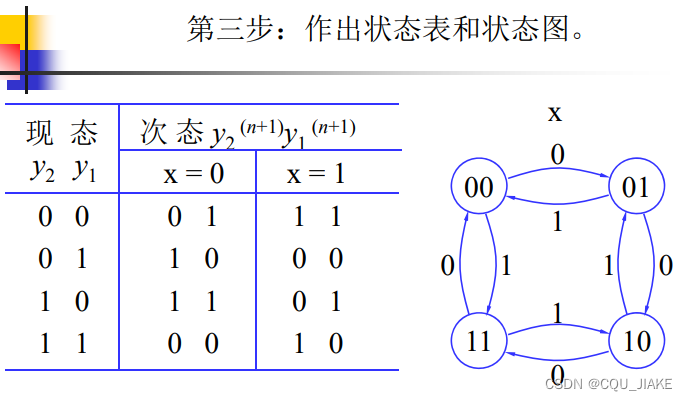
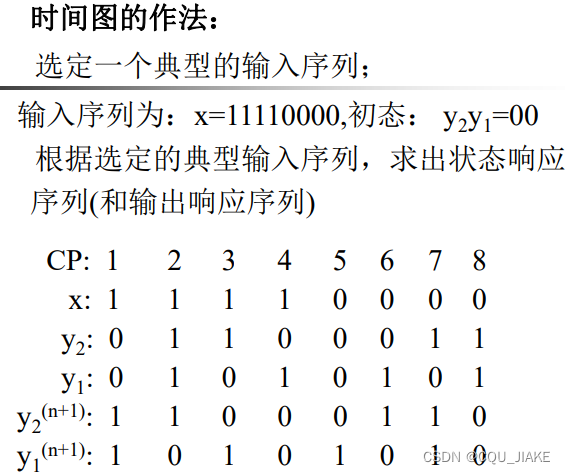
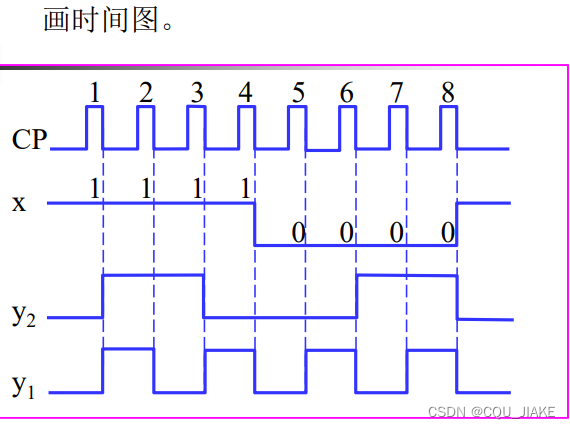
eg2代数法
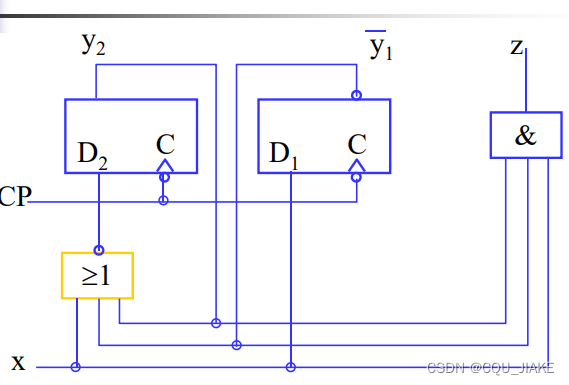
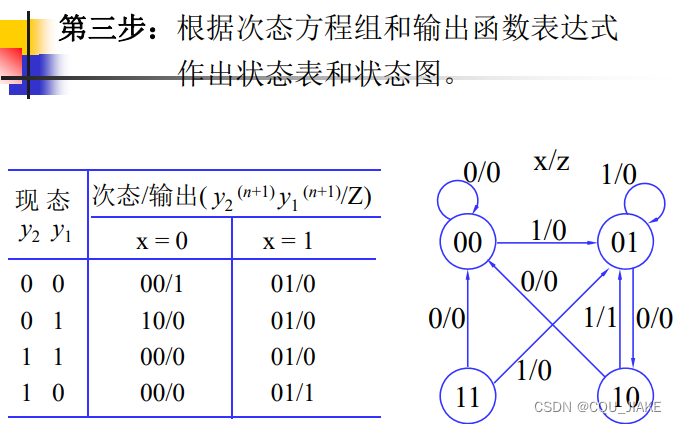
输出和状态是区分开的，输出和状态都是由现态，输入变量决定的，但根本是由输入变量决定的，状态的改变基于原状态和输入变量，即次态方程由现态和输入决定，输出方程亦有现态和输入决定
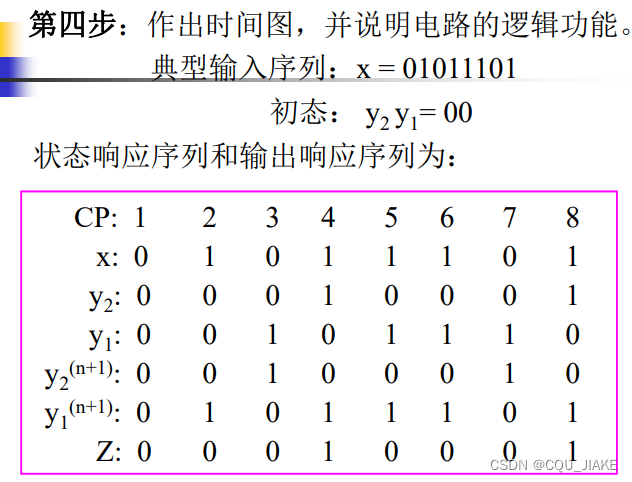
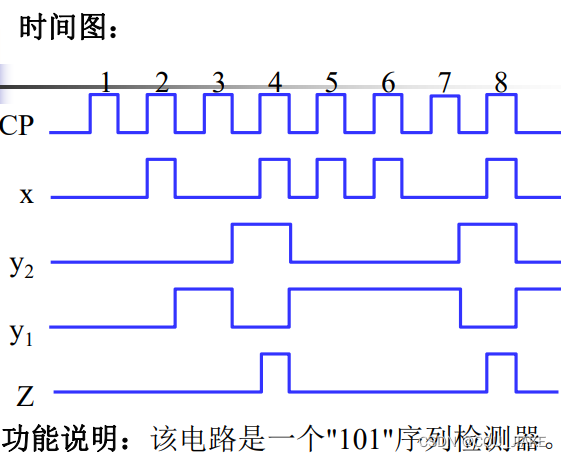
eg
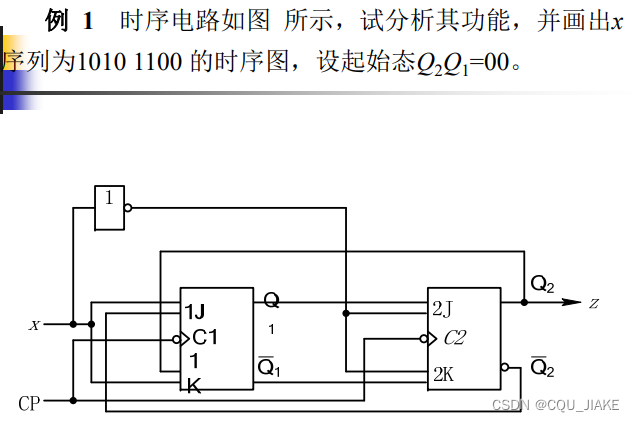
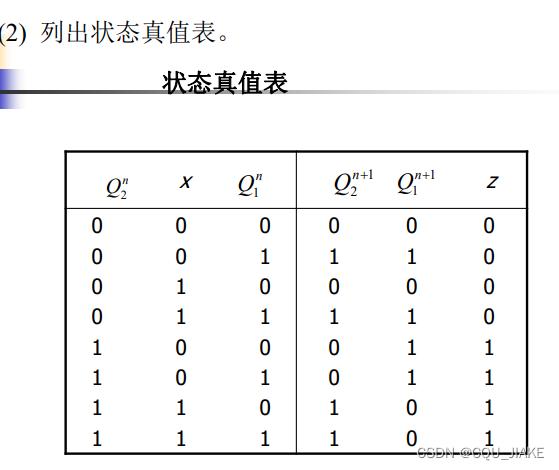
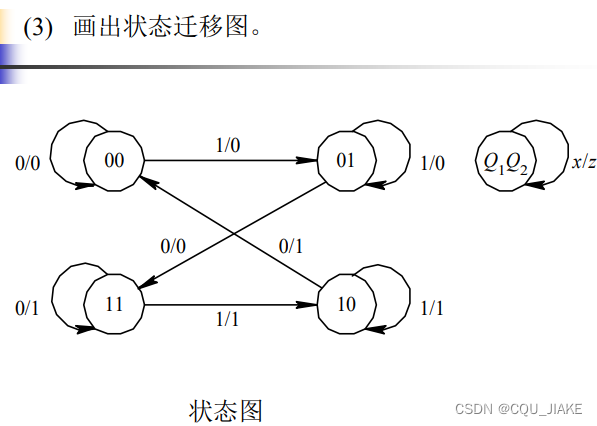
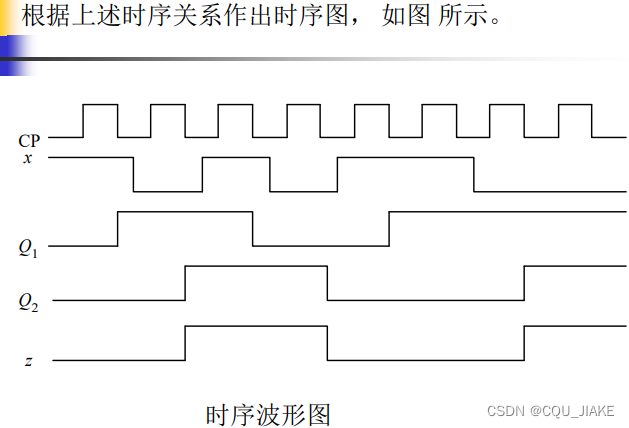
例二
一个输入端有多个信号直接输入时，为与的关系
次态方程由触发器的类型与输入信号直接决定
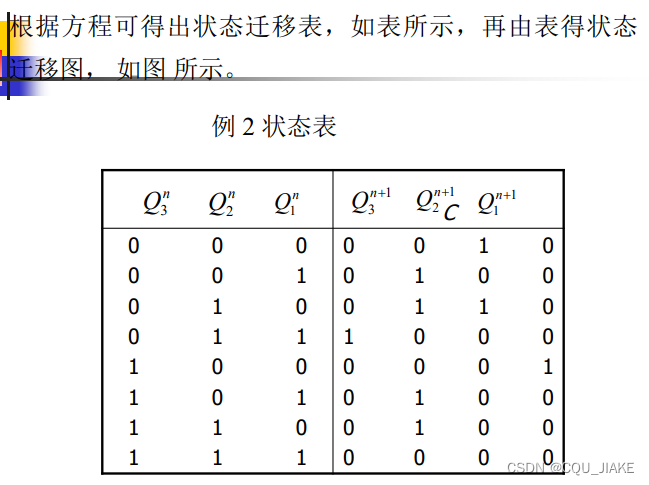
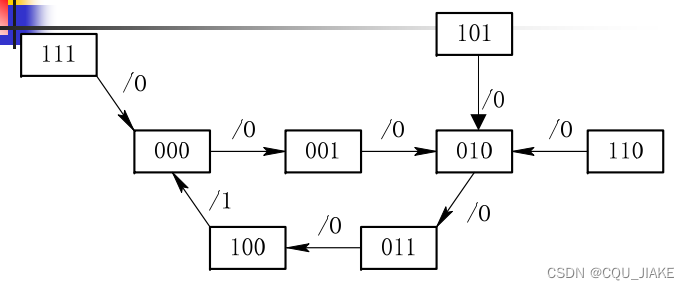
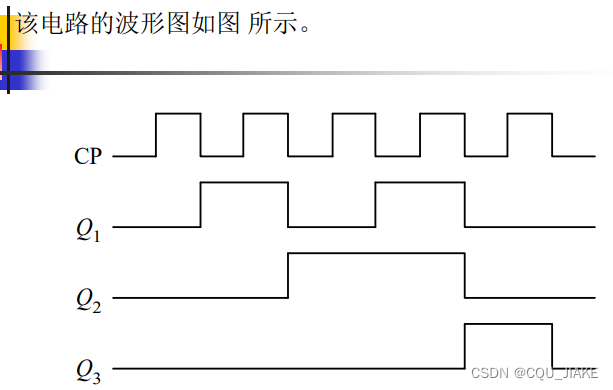
总结一下就是，看电路，看电路有哪些元件，哪些锁存器，然后看那些锁存器的输入输出是什么，都写出来，还要看电路整体的输入、输出信号。
之后就是建立在这些方程上，枚举出所有可能的情况，用一个表，一个图去画
写次态方程时，要消去锁存器的符号，即用锁存器对应的输入信号代替掉（代入），写出次态与输入和现态间的关系
例三
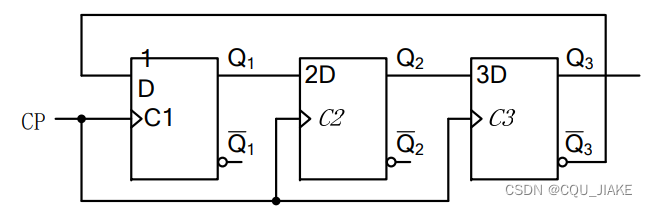
所谓激励方程，就是每个触发器的输入信号是什么，用现态去表示，
次态方程，就是根据触发器的输入信号，消掉触发器的符号，即由激励去表示，用现态与输入信号去确定次态
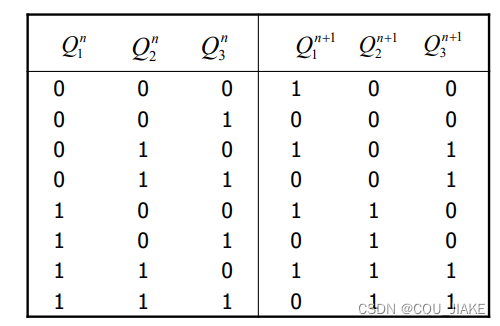
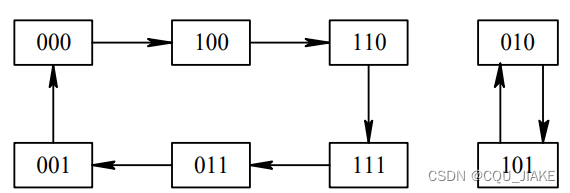
分频电路是将输入的高频信号变为低频信号输出 ，即一个T内，高频信号能有6次周期，转化后，只来一次周期
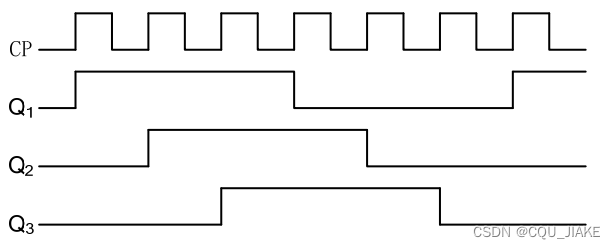
同步时序电路设计
eg
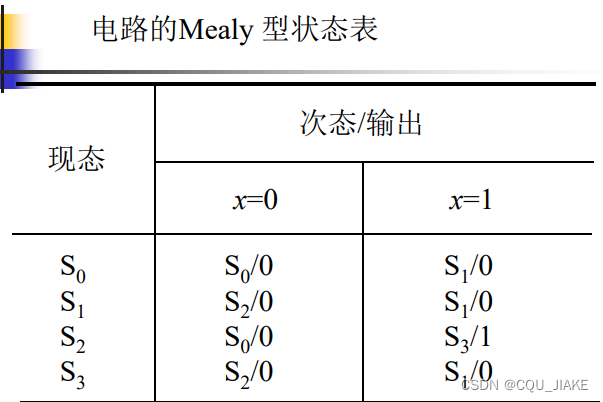
这里s3可以直接忽略掉，被s1替换
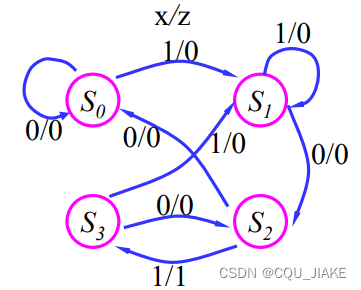
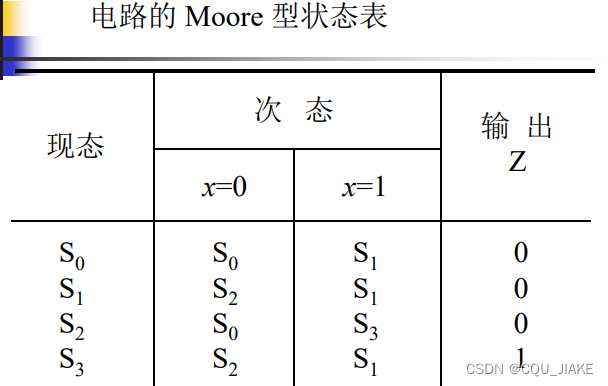
例二
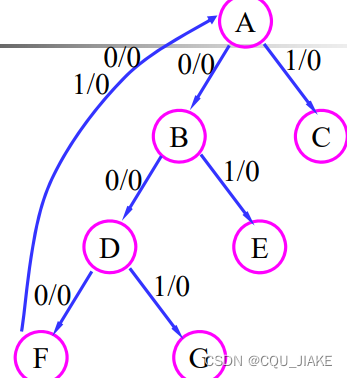
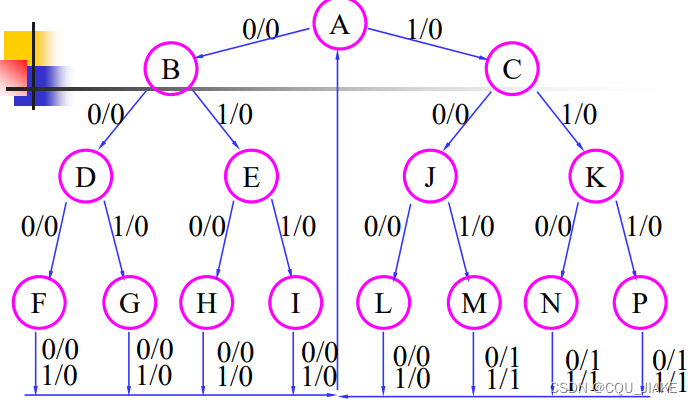
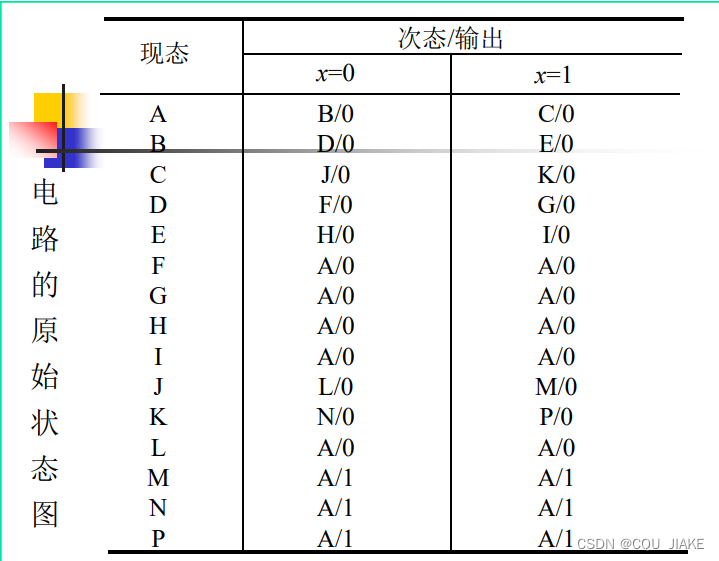
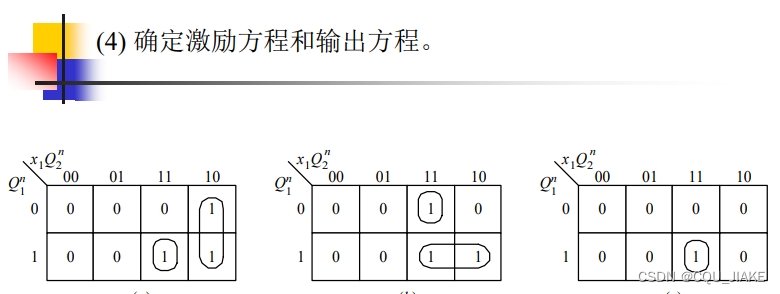
T触发器的激励与输出函数
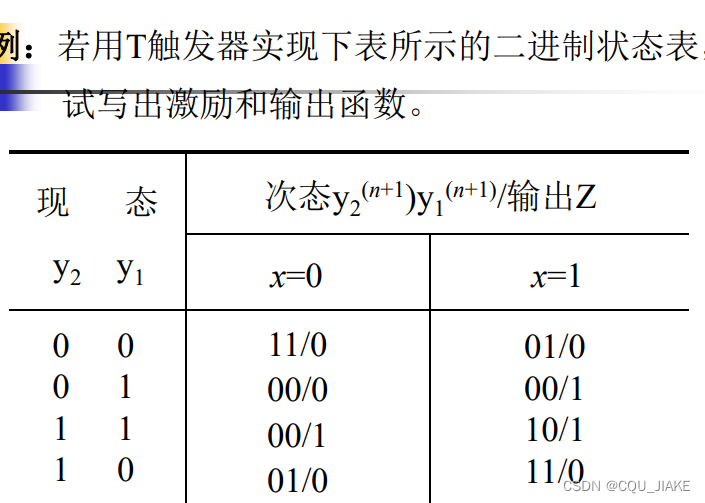
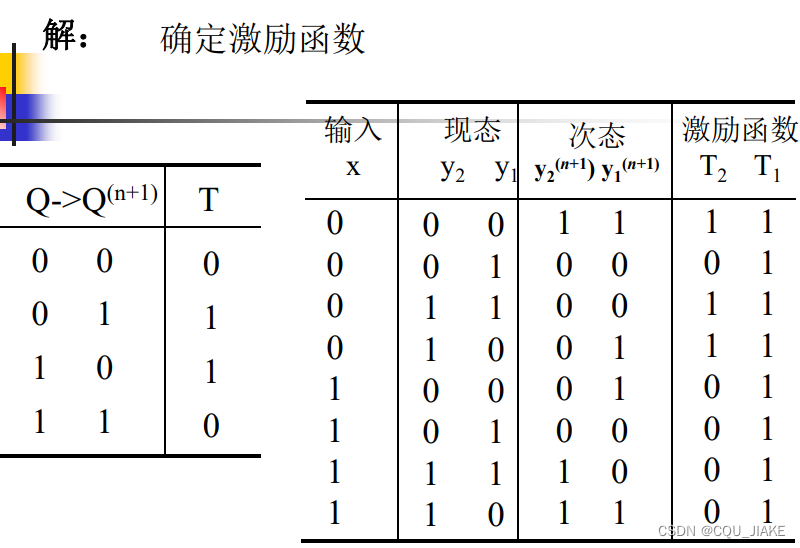
由次态和现态确定T触发器的信号，即激励，然后由卡诺图，确定输入与现态和激励之间的关系
即自变量（两侧方框是现态与输入信号的组合），格子里的值是激励信号
有几个激励，就要画几个卡诺图
输出信号同理，也是画卡诺图，两侧为输入与现态，格子里为输出信号
通过卡诺图就可以找到输出信号、次态与输入信号，现态之间的关系、方程
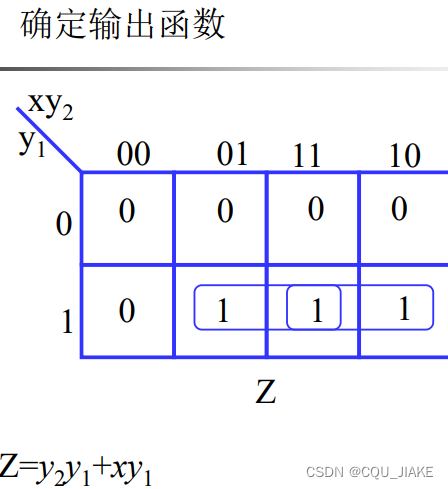
eg
就是有了激励方程（确定的是触发器的输入信号），输出方程后，让现态该怎么组合就怎么组合，该过什么门组合成什么信号就组合成什么信号后连到触发器输入端、电路输出端
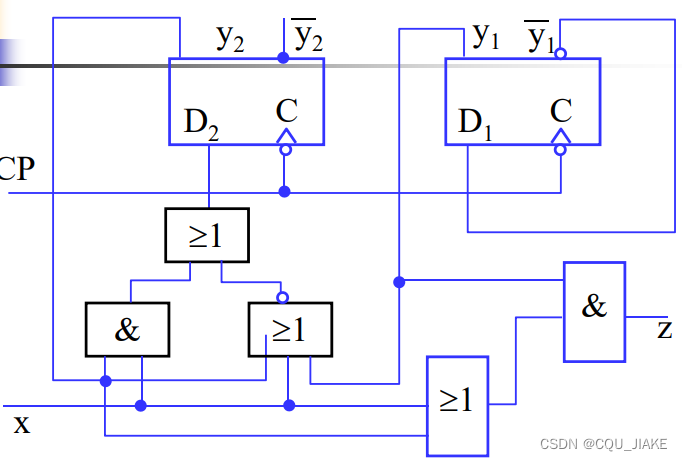
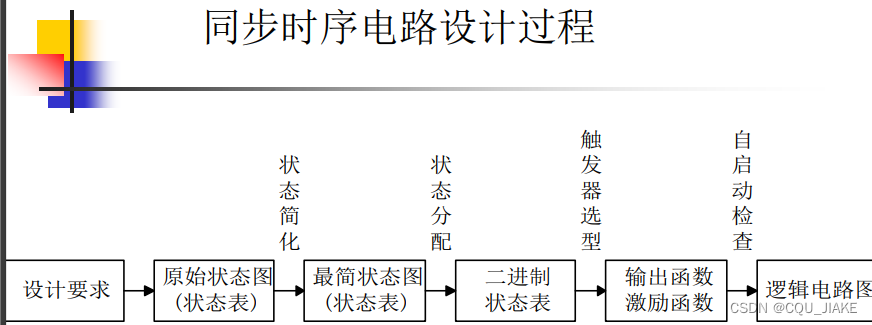
例一
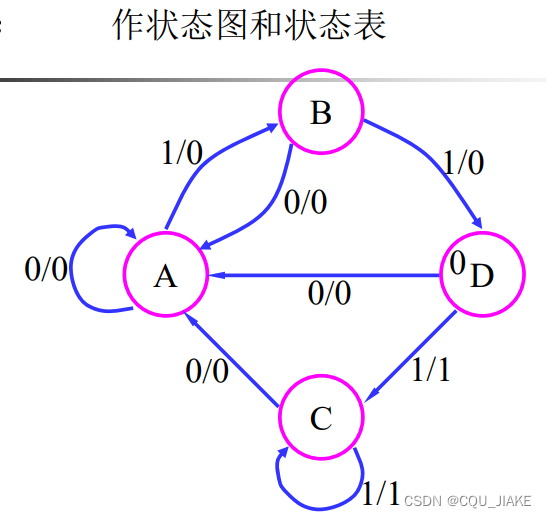
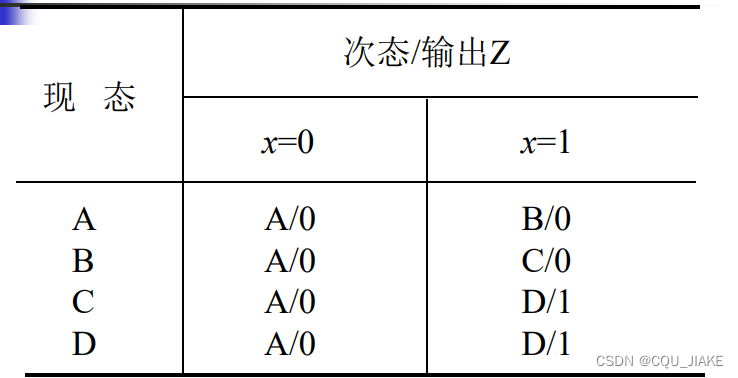
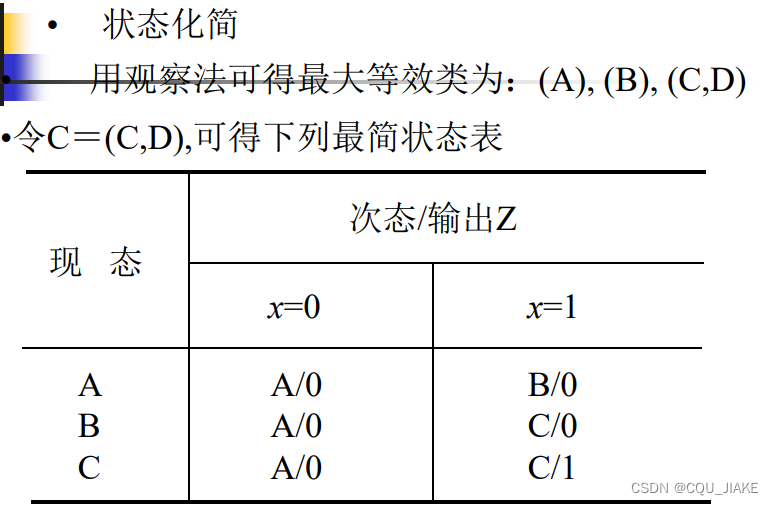
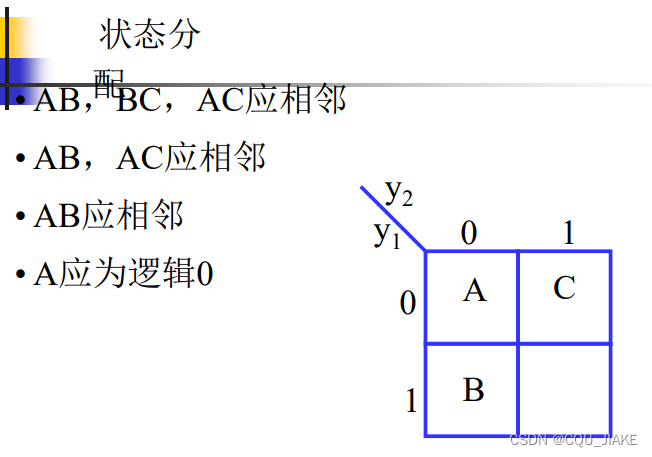
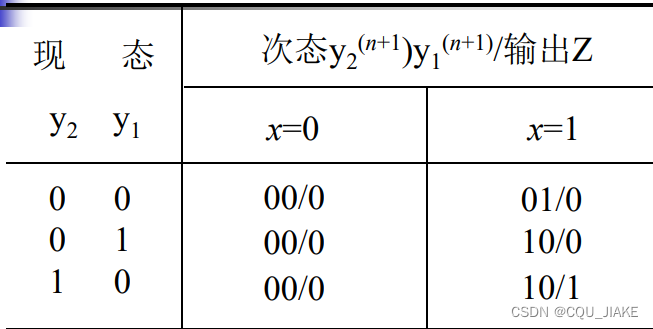
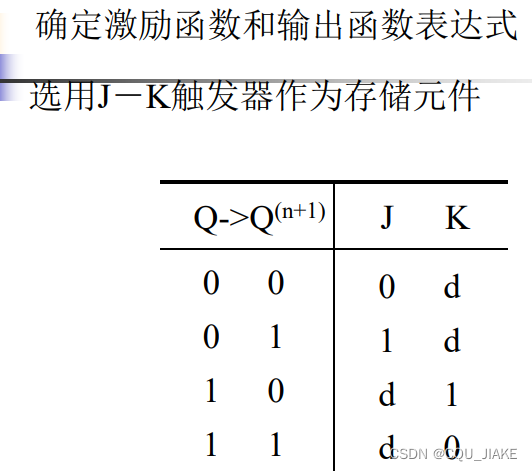
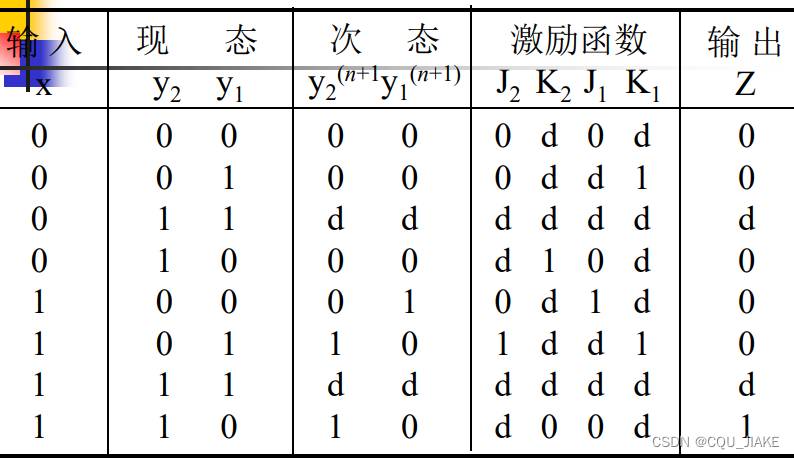
可直接根据图中激励对应为1时，现态、输入信号的取值组合在一起，若有多种情况就或起来，d可以当成1来处理，目的是为了得到最简的
输入、现态——激励信号——次态、输出
要确定次态，就需要激励信号通过触发器得到，具体方式又与触发器类型有关，故而应建立的是激励与输入、现态之间的关系，然后再由激励作为输入信号通过具体的触发器类型得到输出信号，无法直接一步到位
输出信号可直接由输入信号、现态通过门得到，能一步到位
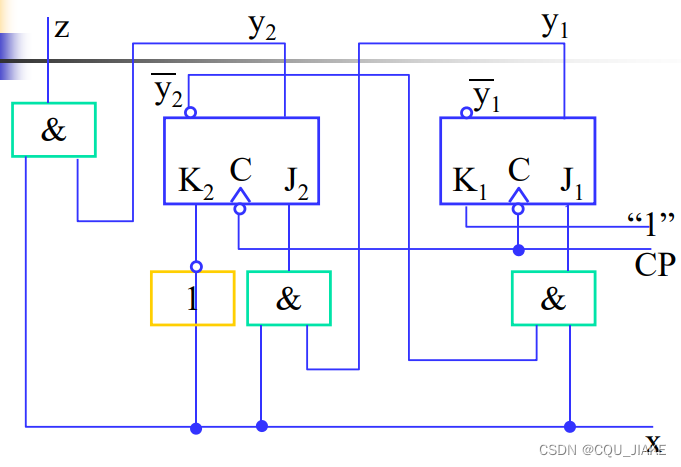
eg:
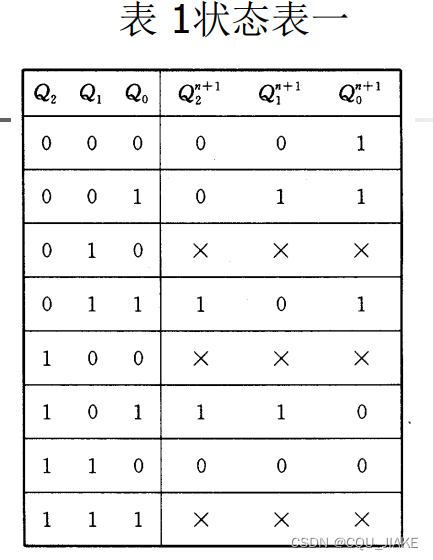
根据现态（无输入信号）确定
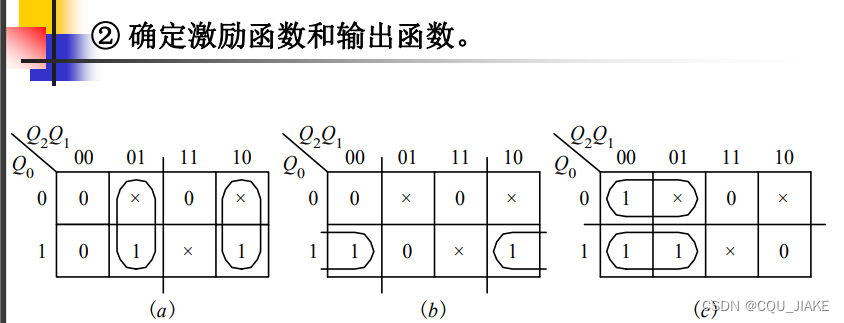
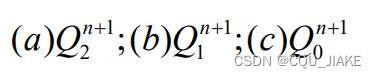
设计的话就是先根据现态和输入确定好了方程，即次态与现态、输入的关系，再去选择的触发器实现，即在已有方程的基础上选择触发器
那就是看方程形式和几种基础触发器的方程哪个更相像
这可以直接无脑选D触发器，即让等式右边的现态、输入一坨根据其方程综合出一个信号，让其作为D信号的激励
这里选择J-K触发器，应该是可以减少门的使用数量
自启动检查
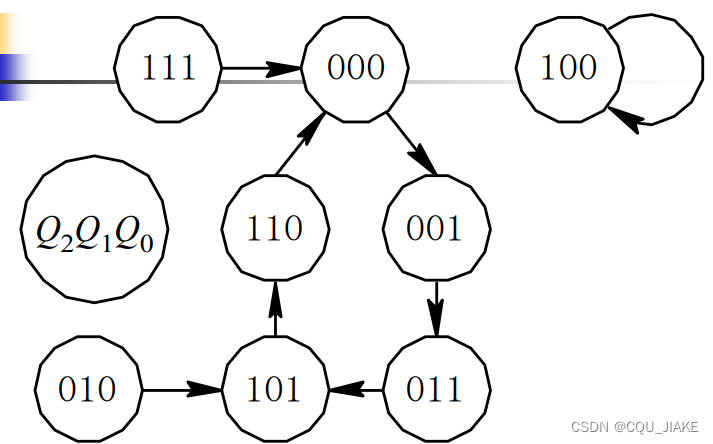
非完全描述，就是因为出现了任意项
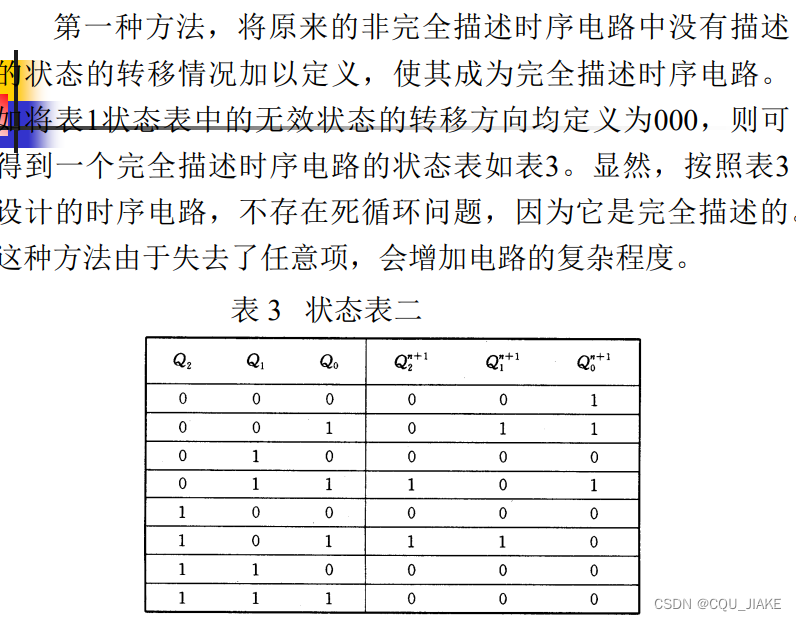
第二种方法就是说还是在原图画，保留任意项，但是同试试其他的画法，可能就不会出现问题了
EG
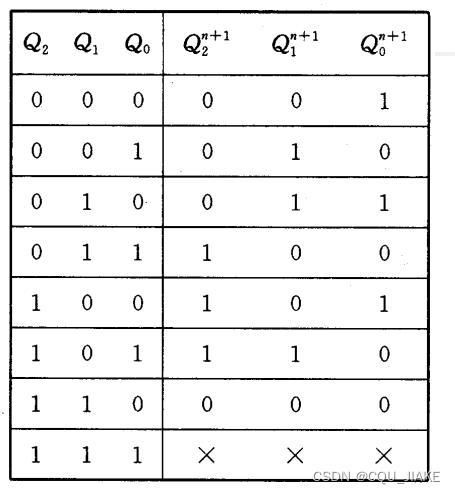
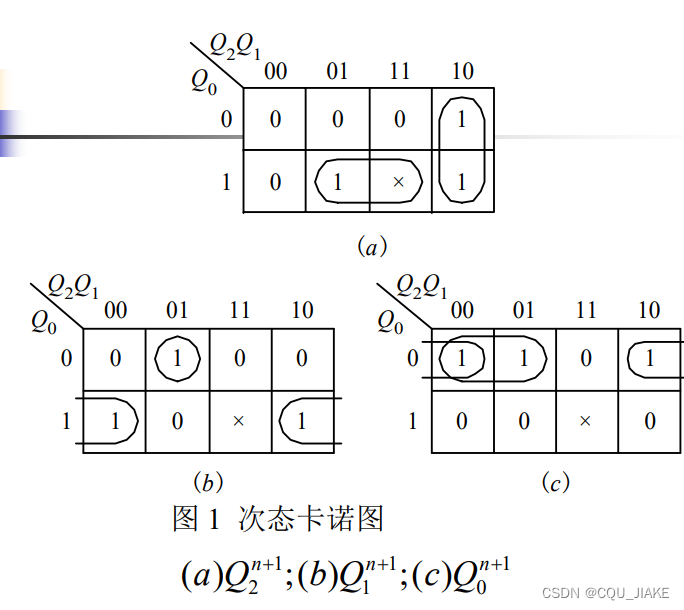
卡诺图确定，找不变的
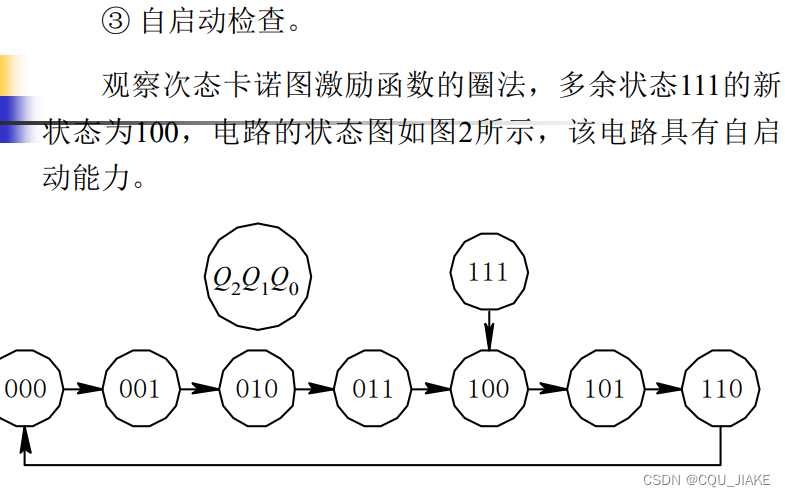所谓自启动，就是假定电路状态在任意一个状态时启动，检查其是否还能正常工作，这就要求最大连通数为1，不能有两个连通分图
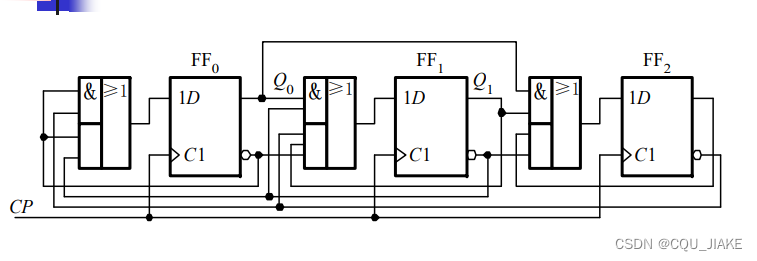
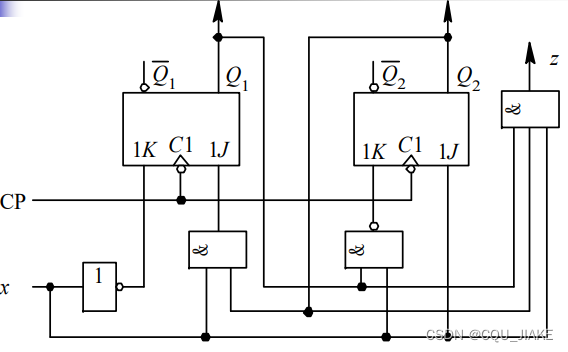
先画几个触发器，触发器的输出即是现态，输入即是激励方程所求的一坨，要让触发器的输出经过门的组合电路来组合，触发器的输出还要过一个组合电路来组合出这个状态（现态）下 的输出，最后就是把时钟信号连接到各个触发器的时钟端
EG
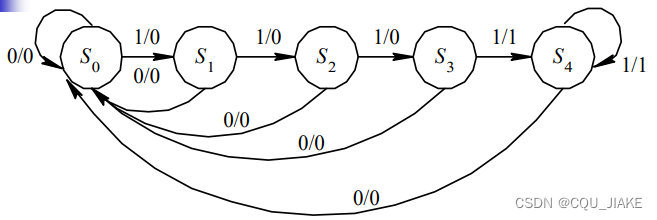
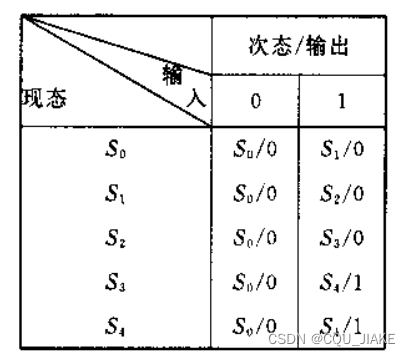
s3可被简化掉
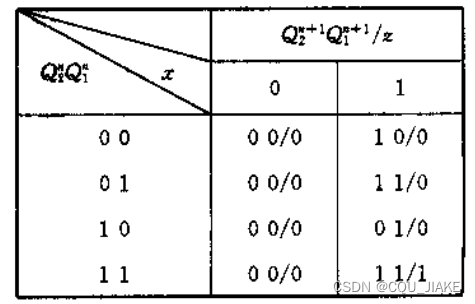
EG
BCD
BCD码就是用4个二进制位表示一个十进制数，由于4个二进制位可以表示16种状态（0~15），而一个十进制数有10种状态（0~9），所以多出6种状态，故BCD码有多种
8421码就是前10种，余三码就是整体往后移3位，即3~12位（共12-3+1=10个数）
有几个状态变量就要几个触发器，每个触发器可能有多个激励信号，但每组激励信号只能作用于一个触发器，只能确定一个状态变量
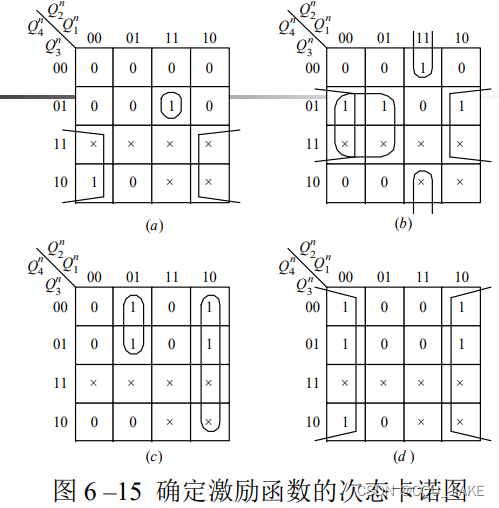
四个状态分量Q1Q2Q3Q4
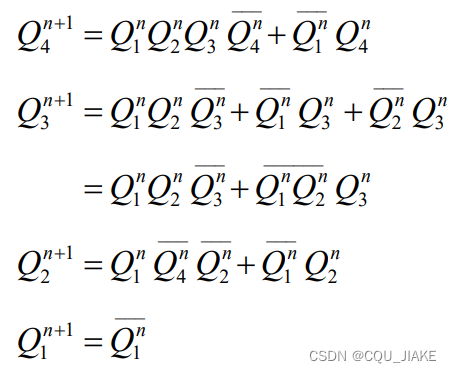
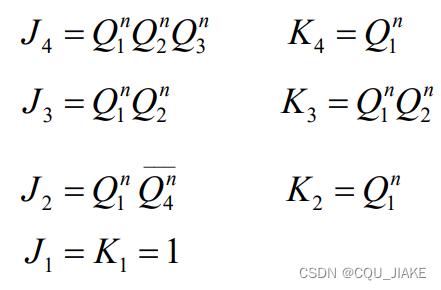
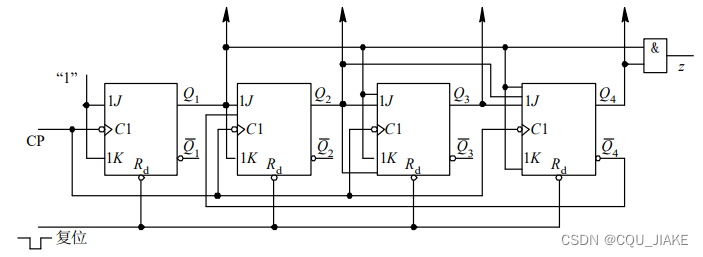
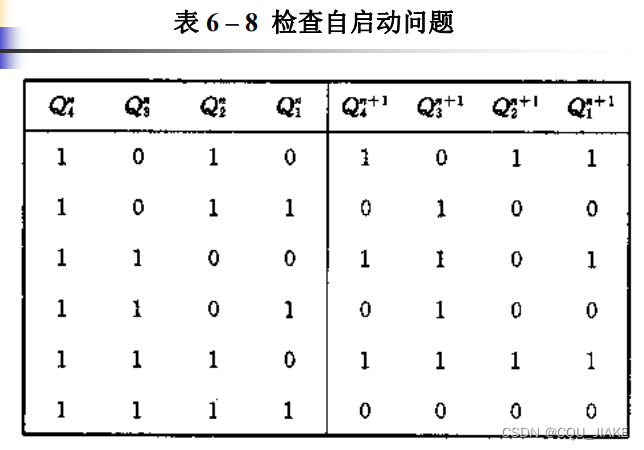
检查自启动就是要让无关状态被涵盖在连通图里，即可以到达主循环里，而不是自成一派，
如果无法自启动，就要尝试换一种卡诺图取法，以求使状态图发生改变
EG
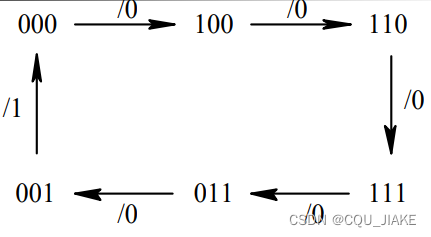
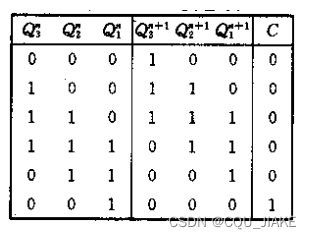
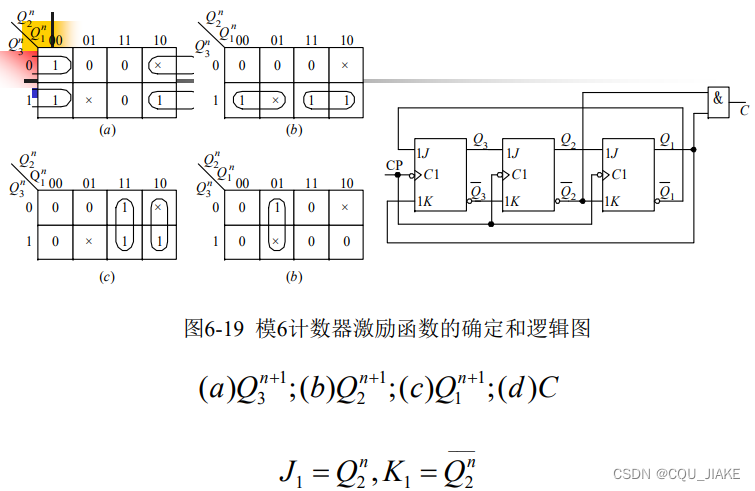
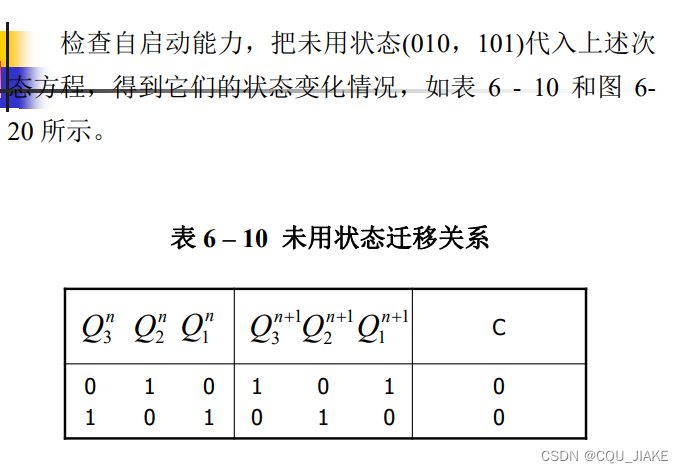
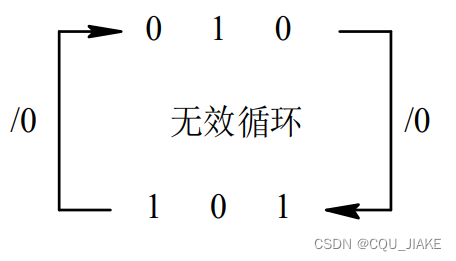出现了自成一派，连通分支数大于1，无法自启动
Q1非+Q2非=Q1&Q2非，即Q1没发生或Q2没发生等价于Q1且Q2没发生，非或转化为与或
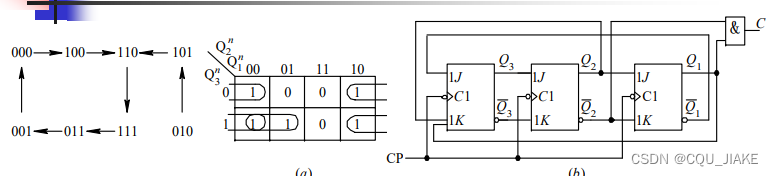
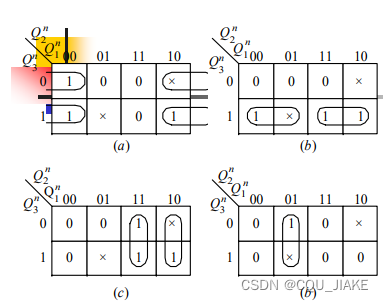原本是这样画的，无法自启动，就换一种画法，尽可能多用任意项（把其当为1）
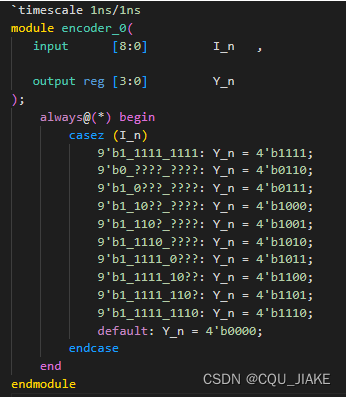
优先编码器
case
case就是该是什么就什么
casez是最后一位为高阻z，z一直为1，如果输入为z，那么直接全1，
casex不是最后一位的x，x，z值都为1，只要出现x或z的值，都会直接全为1
x,z不是未知数，是一种 符号，？代表未知数
casez允许电路使用一个未知数，casex允许使用两个
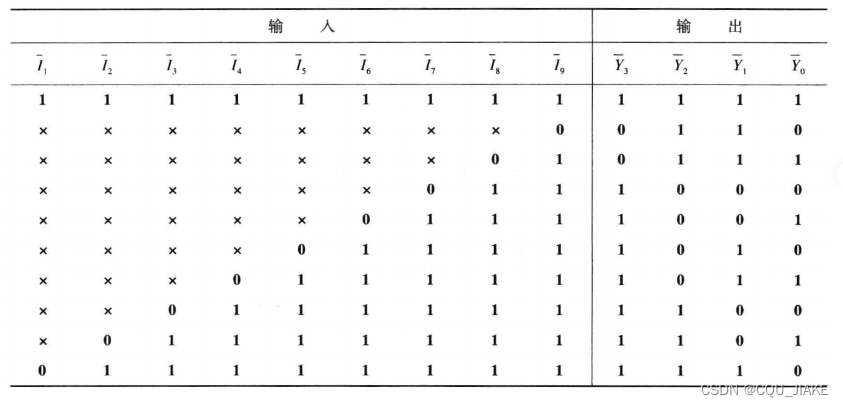
11行开始添加测试样例
