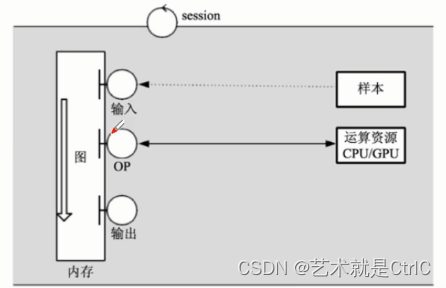
对于序列 { x n } = x 1 , x 2 , ⋯ , x n \{x_n\}= x_1, x_2, \cdots, x_n {xn}=x1,x2,⋯,xn,求其导数 { x n ′ } \{x'_n\} {xn′}。
一、精度 O ( h ) O(h) O(h)
x k ′ = { x 2 − x 1 h , k = 1 x k − x k − 1 h , k = 2 , 3 , ⋯ , n x_k' = \begin{cases} \frac{x_{2} - x_{1}}{h}, k=1 \\ \frac{x_{k} - x_{k-1}}{h}, k=2,3,\cdots, n \\ \end{cases} xk′={hx2−x1,k=1hxk−xk−1,k=2,3,⋯,n
其中,对 k = 1 k=1 k=1时进行处理,保证导数序列长度也为 n n n。
二、精度 O ( h 2 ) O(h^2) O(h2)
也即中心微分算法
x k ′ = { x 2 − x 1 h , k = 1 x k + 1 − x k − 1 2 h , k = 2 , 3 , ⋯ , n − 1 x n − x n − 1 h , k = n x_k' = \begin{cases} \frac{x_{2} - x_{1}}{h}, k=1 \\ \frac{x_{k+1} - x_{k-1}}{2h}, k=2,3,\cdots, n-1 \\ \frac{x_{n} - x_n-{1}}{h}, k=n \\ \end{cases} xk′=⎩ ⎨ ⎧hx2−x1,k=12hxk+1−xk−1,k=2,3,⋯,n−1hxn−xn−1,k=n
三、精度 O ( h 4 ) O(h^4) O(h4)
x k ′ = { x 2 − x 1 h , k = 1 x 3 − x 1 2 h , k = 2 − x k + 2 + 8 x k + 1 − 8 x k − 1 + x k − 2 12 h , k = 3 , ⋯ , n − 2 x n − x n − 2 2 h , k = n − 1 x n − x n − 1 h , k = n x_k' = \begin{cases} \frac{x_{2} - x_{1}}{h}, k=1 \\ \frac{x_{3} - x_{1}}{2h}, k=2 \\ \frac{-x_{k+2} + 8 x_{k+1} - 8 x_{k-1} + x_{k-2}}{12h}, k=3,\cdots, n-2 \\ \frac{x_{n} - x_{n-2}}{2h}, k=n-1 \\ \frac{x_{n} - x_n-{1}}{h}, k=n \\ \end{cases} xk′=⎩ ⎨ ⎧hx2−x1,k=12hx3−x1,k=212h−xk+2+8xk+1−8xk−1+xk−2,k=3,⋯,n−22hxn−xn−2,k=n−1hxn−xn−1,k=n
四、比较
设 x = sin ( t ) x=\sin(t) x=sin(t),真实导数为 cos ( t ) \cos(t) cos(t),离散采样作比较。当 T s = 0.1 T_s=0.1 Ts=0.1 时如下,可见直接微分精度较低。
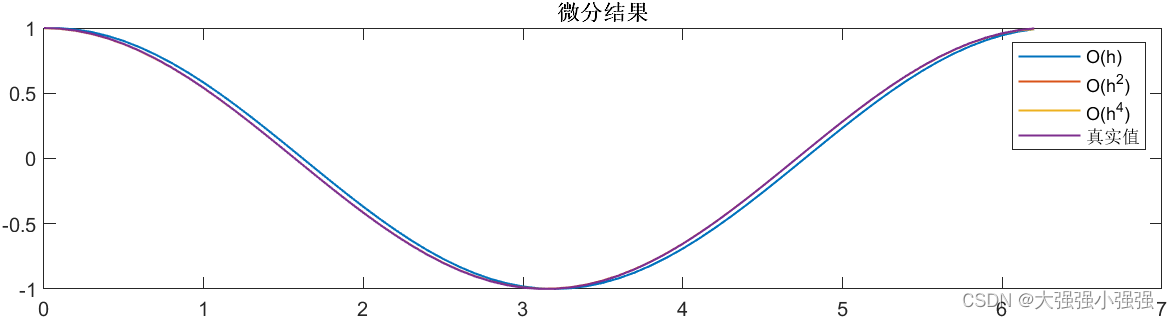
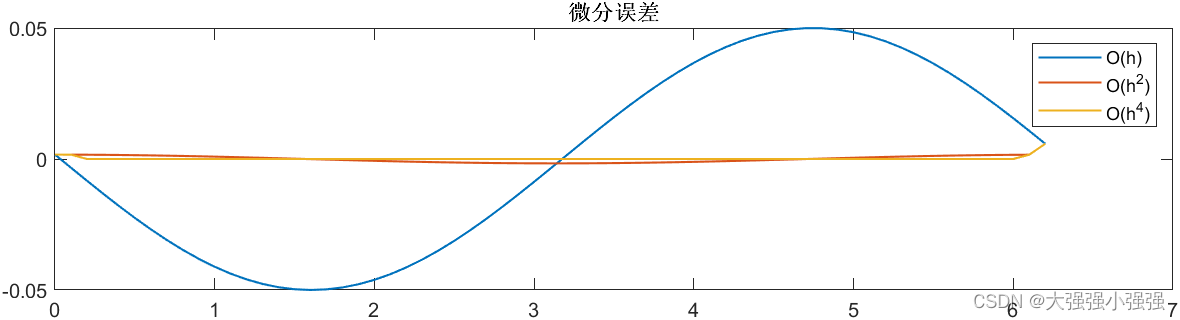
采样时间为 T s = 1 T_s=1 Ts=1 时如下
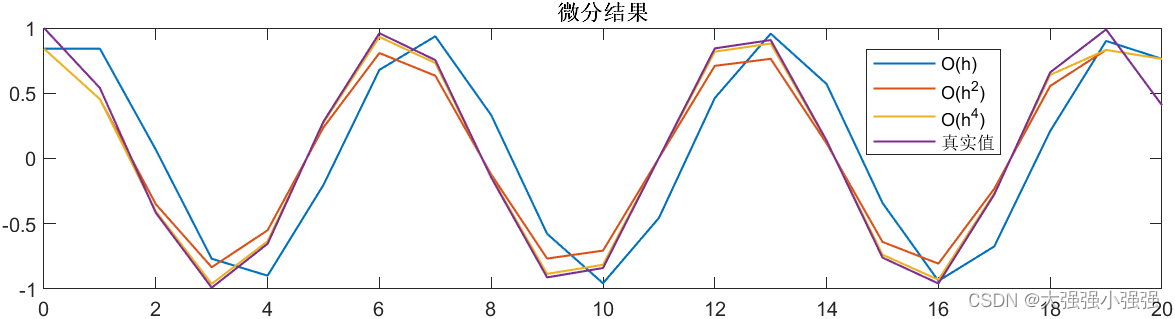
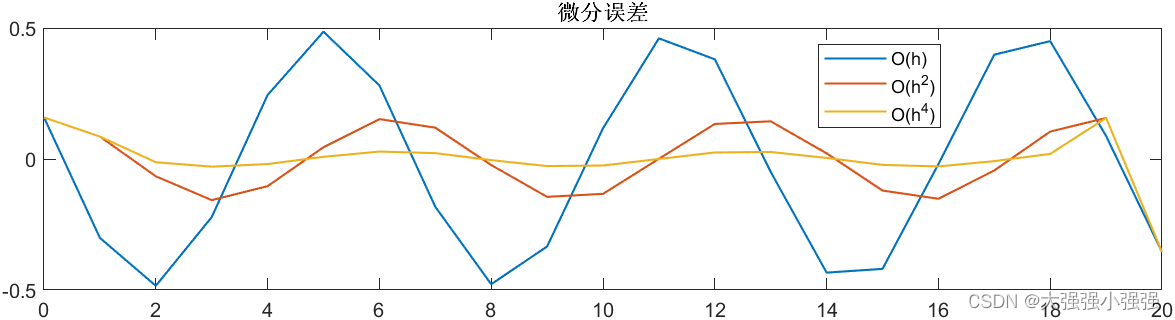
结论:很多时候中心微分就够了
代码如下
Ts = 1;
t = 0:Ts:20;
N = length(t);
t = reshape(t, [N,1]);
x = sin(t);
dx = cos(t);
dx1 = diff_1st(x, Ts);
dx2 = diff_2nd(x, Ts);
dx3 = diff_4th(x, Ts);
subplot(211);plot(t, dx1, t, dx2, t, dx3, t, dx, 'linewidth',1)
legend('O(h)', 'O(h^2)', 'O(h^4)', '真实值')
title('微分结果')
subplot(212);plot(t, dx-dx1, t, dx-dx2, t, dx-dx3, 'linewidth',1)
legend('O(h)', 'O(h^2)', 'O(h^4)')
title('微分误差')
function dx = diff_1st(x, dt)
dx = (x(2:end) - x(1:end-1)) / dt;
dx = [dx(1); dx];
end
function dx = diff_2nd(x, dt)
dx = (x(3:end) - x(1:end-2)) / (2*dt);
dx1 = (x(2)-x(1)) / dt;
dxend = (x(end)-x(end-1)) / dt;
dx = [dx1; dx; dxend];
end
function dx = diff_4th(x, dt)
dx = (-x(5:end) + 8 * x(4:end-1) - 8 * x(2:end-3) + x(1:end-4)) / (12 * dt);
dx2 = (x(3) - x(1)) / (2*dt);
dx1 = (x(2) - x(1)) / dt;
dx_end2 = (x(end) - x(end-2)) / (2*dt);
dx_end1 = (x(end) - x(end-1)) / dt;
dx = [dx1; dx2; dx; dx_end2;dx_end1];
end