目录

目录：

        1:快速排序的思想

        2:快速排序的三种形式

        3:快速排序的优化方法

---

    前言：快速排序是一种非常重要的排序我们需要掌握它，当然肯定也相比前面的那些排序有一定的难度，但是相信本篇文章会让你对快排有重新的理解，让快排变得不再那么难！！让我么一起加油吧！！

1：快速排序的思想

        在这里我们是用快速排序排升序！

        其实快速排序的思想与我们之前学过的二叉树的知识有点联系，快速排序一趟思想主要是遍历一遍数组，确定一个数的位置，我们假设这个位置是keyi，一般keyi的值为区间最左边的值，我们就是让在keyi左边数的值全部小于这个位置处的值，即小于a[keyi]，在keyi位置右边的值全部大于a[keyi]。这样说可能还是有点抽象，我们借用图来理解一下这个思想。

        在这一趟快排结束后我们就在数组中确定了一个数的位置，且这个数的位置在之后的操作不需要管了。

快排的总思想：采用了分治的思想，就是对数组进行多次的排序，让小区间有序，最后整体就会有序了。如图

        总结：快速排序是采用了分治的思想，一趟快速排序能够确定一个数的位置，然后我们只需要将该位置处左边的数组有序，与右边有序，那么整体就会有序了。

        下面让我们来手撕一下快速排序的底层具体代码吧！！

  2：快速排序的三种方法

        说实话，可能我们在平时面试的时候可能只需要掌握一种情况就可以了，但是当我们在学习的时候我们就要增加自己的内功，多认识几种方法总会是好的~~

        这些代码我们已近加上了三数取中的优化方法，至于为啥可以看到第三个标题哦。

        1:hoare提出的

        我们先直接上代码，然后我们来一起手撕这个代码！

                

void QuickSort1(int* a, int left,int right)
{
	//[begin,end],控制区间用来递归
	int midi = GetMidi(a, left, right);
	Swap(&a[midi], &a[left]);
	if (left >= right)
		return;
	int begin = left;
	int end = right;
	int keyi = left;
	while (begin < end)
	{
		//右边找小
		while (begin < end && a[end] >= a[keyi])
		{
			end--;
		}

		//左边找大
		while (begin < end && a[begin] <= a[keyi])
		{
			begin++;
		}
		Swap(&a[begin], &a[end]);

	}
	Swap(&a[keyi], &a[begin]);
	
	QuickSort1(a, left,begin-1);
	QuickSort1(a, begin + 1,right);
}

hoare大佬的思想是这样子的：首先定义两个指针，一左一右  我们姑且就认为是begin与end吧！，先假设keyi的位置为left处的位置，然后让右指针先走找到比a[keyi]值小的，在左指针走找大于a[keyi]处的值，然后交换a[begin]与a[end]，然后循环的寻找，直到begin与end相遇我们才认为我们的循环结束，最后在交换a[keyi]与a[begin]或者是a[end]因为在相遇位置处一定是begin==end的。

        代码要注意的点：第一个我们因该保留的是key位置的下标，不然在进行交换的时候我们不能将数组中的两个位置交换，他可能只是数组中的1个值与key变量进行交换。

        第二个就是我们在使用内部循环的时候要注意begin要小于end如果不小于的话，那可能我们的数组会形成越界，

        我们通过图来解析这个思路

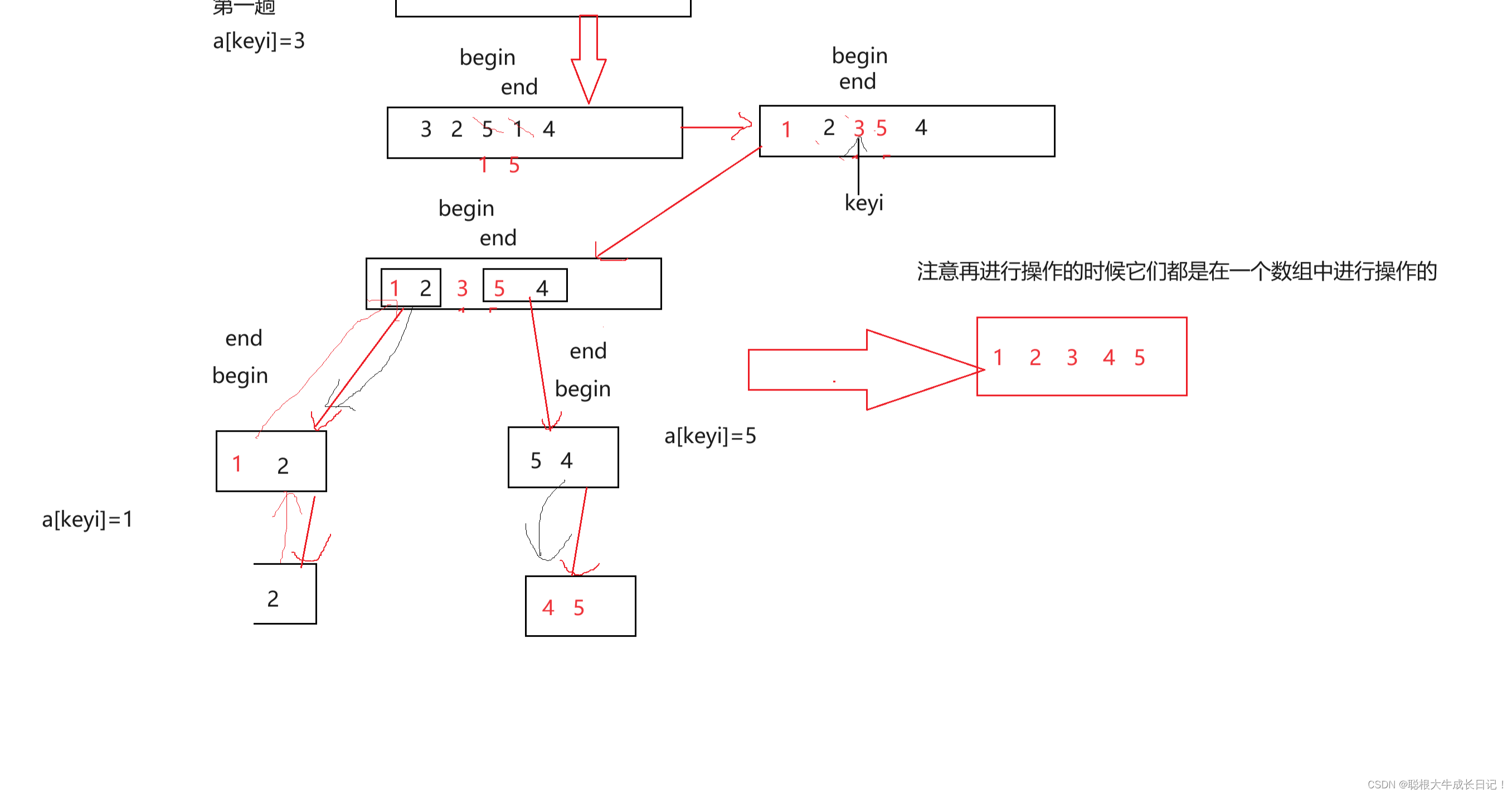如果你没看懂这个图的话，建议拿着代码在去动手画一下图。就应该能懂了。

        

2挖坑法

        老规矩还是先上代码：

        

void QuickSort3(int* a, int left, int right)
{
	int midi = GetMidi(a, left, right);
	Swap(&a[midi], &a[left]);
	//先将第一个坑给挖出来，并且值保留
	if (left >= right)
	{
		return;
	}

	int key = a[left];
	int hole = left;
	int end = right;
	int begin = left;
	while (begin < end)
	{
		//右边找小
		while (begin < end && a[end] >= key)
		{
			end--;
		}
		//将找到小的值，移动到坑处
		Swap(&a[hole], &a[end]);
		hole = end;
		//左边找大
	while (begin < end && a[begin] <= key)
		{
			begin++;
		}
		Swap(&a[hole], &a[begin]);
		hole = begin;

	}
	a[hole] = key;

	QuickSort3(a, left, hole - 1);
	QuickSort3(a, hole + 1, right);

}

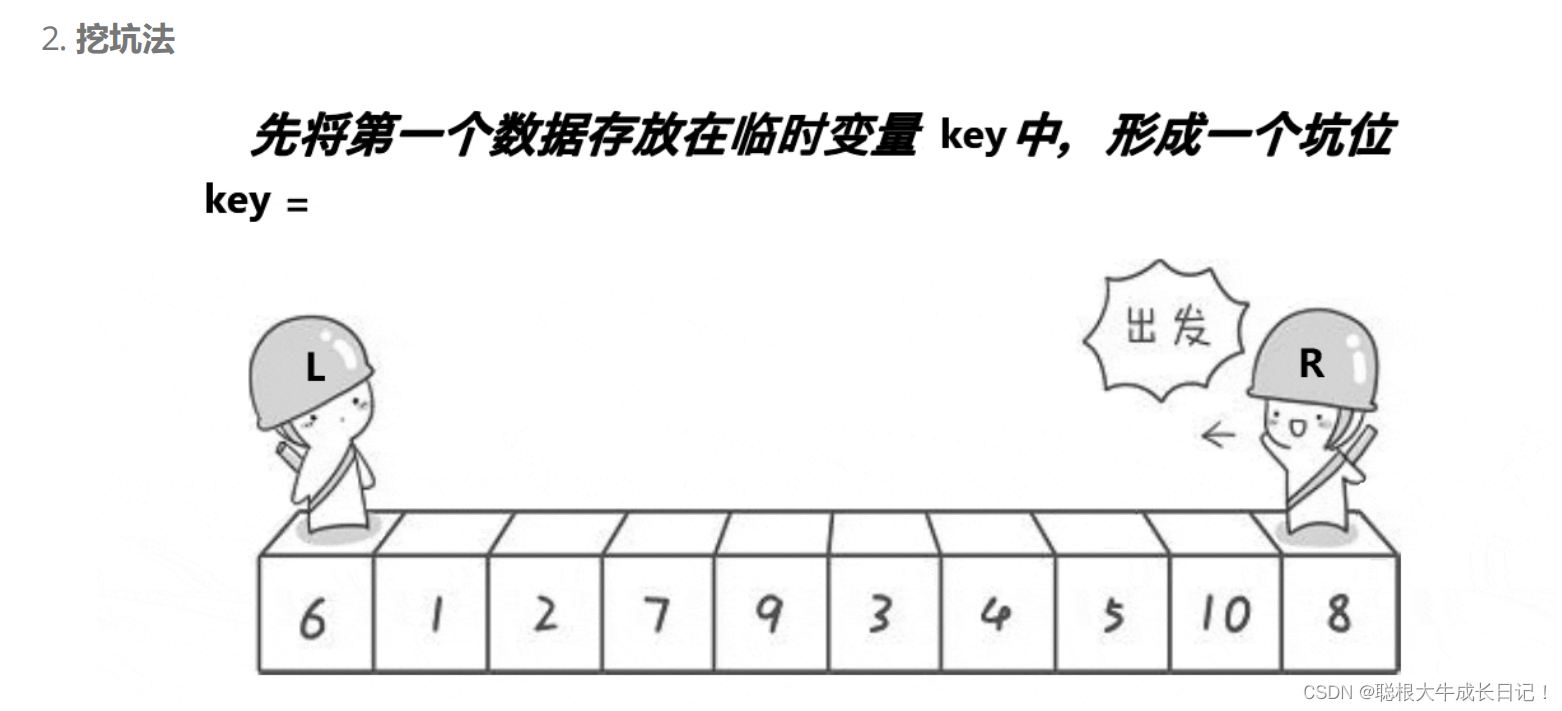
挖坑法其实本质上只是hoare方法的一种优化，它是首先将数组中第一个数的值放到一个key变量的值，在图上就是将6放到key变量中，这样我们假设我们的数组形成了一个坑位，还是采用老方法，一左一右两个指针，但是与hoare方法不同的思想就在于：右边找小，找到小了我们就将这个值放到坑位上去，然后我们将坑位变成右边这个指针处，然后左指针开始找大，找到大的值后我们将它放入坑中，在将坑位变成左指针处，循环的进行下去，直到左指针==右指针，最后我们在将key放入坑位中，这样我们的一趟快速排序就完成了，我们在采用分治的思想递归坑的左边，递归坑的右边，当递归完成的时候我们的快速排序也就完成了.

   这里我们就用图来画一趟内部的快速排序！

             

 3双指针法

void QuickSort2(int* a, int left, int right)
{
	if (left >= right)
		return;
	int midi = GetMidi(a, left, right);
	Swap(&a[midi], &a[left]);

	
	int prev = left;
	int cur = prev + 1;
	int keyi = left;
	while (cur <=right)
	{
		//cur找小，找到小，先++prev然后在交换
		if (a[cur] < a[keyi])
		{
			++prev;
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[keyi], &a[prev]);
	QuickSort2(a, left, prev - 1);
	QuickSort2(a, prev+1, right);

}

前后指针的一趟思想：

        我们先定义一个prev指针指向要分治数组的左边，在定义一个cur指针它的值等于prev指针+1，定义一个keyi为数组的左边的值，cur指针找小，当cur找到小的时候我们就先++prev指针，然后在与cur指针进行交换，当cur大于keyi的值时，我们就++cur就行，当cur大于数组最后一个值的下标时，我们的一趟循环就结束了。

        我们上一个动图来与该思路一起配合起来。

在这里我们就将快速排序的3种思想就讲解完毕了！

  如果还有不懂得小伙伴可以私信我哦！！

3：快速排序的优化

        我们知道，快速排序的时间复杂度最坏的情况下就是要排序数组是逆序的，此时快速排序的时间复杂度为O(N^2)的，为啥是这样呢？因为我们在这种情况下我们遍历一遍数组选择一个位置，所以总的来说就是O(N^2),但是在平常我们在使用的时候为什么我们说快速排序的时间复杂度是O(N*logN)呢，因为我们对三面三种情况下的代码都增加了三数取中的思想，这样能够是我们呢的快速排序形成分治的思路。防止了逆序的出现。

        代码如下：

        优化方法1：三数取中

        相信三数取中的代码的思想不是很难我们返回的是数组的下标哦，我们只需要两两进行比较就行了。

int GetMidi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	// left mid right
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])  // mid是最大值
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right]) // mid是最小
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

优化方法2:减少递归的调用次数

        我们知道递归是在栈区进行的，而栈区的空间相对于其它区域的空间来说，它并不是很大的，所以当我们递归的高度过多的时候我们的函数就会出现栈溢出的bug。

        那我们如何优化？

        首先我们知道假设我们的数组非常大，我们对他进行快排，当子数组长度非常小的时候我们假设为10，那么这个子数组肯定相对于原来的数组来说，是有序的，这时候我们采用直接插入排序就可以优化我们的快速排序了，好像库里面也是这样实现的。

        那为什么我们要当结点个数小于10的时候就不递归了呢？如下分析

我们知道二叉树中最后一层的结点个数接近数组整个长度的一半，而倒数三层所加起来的结点的个数≈%87.5，所以我们就选用了10这个数字。

        总结优化思路：规定数组大小那些不需要进行优化与直接插入排序的使用。

        代码如下：

        

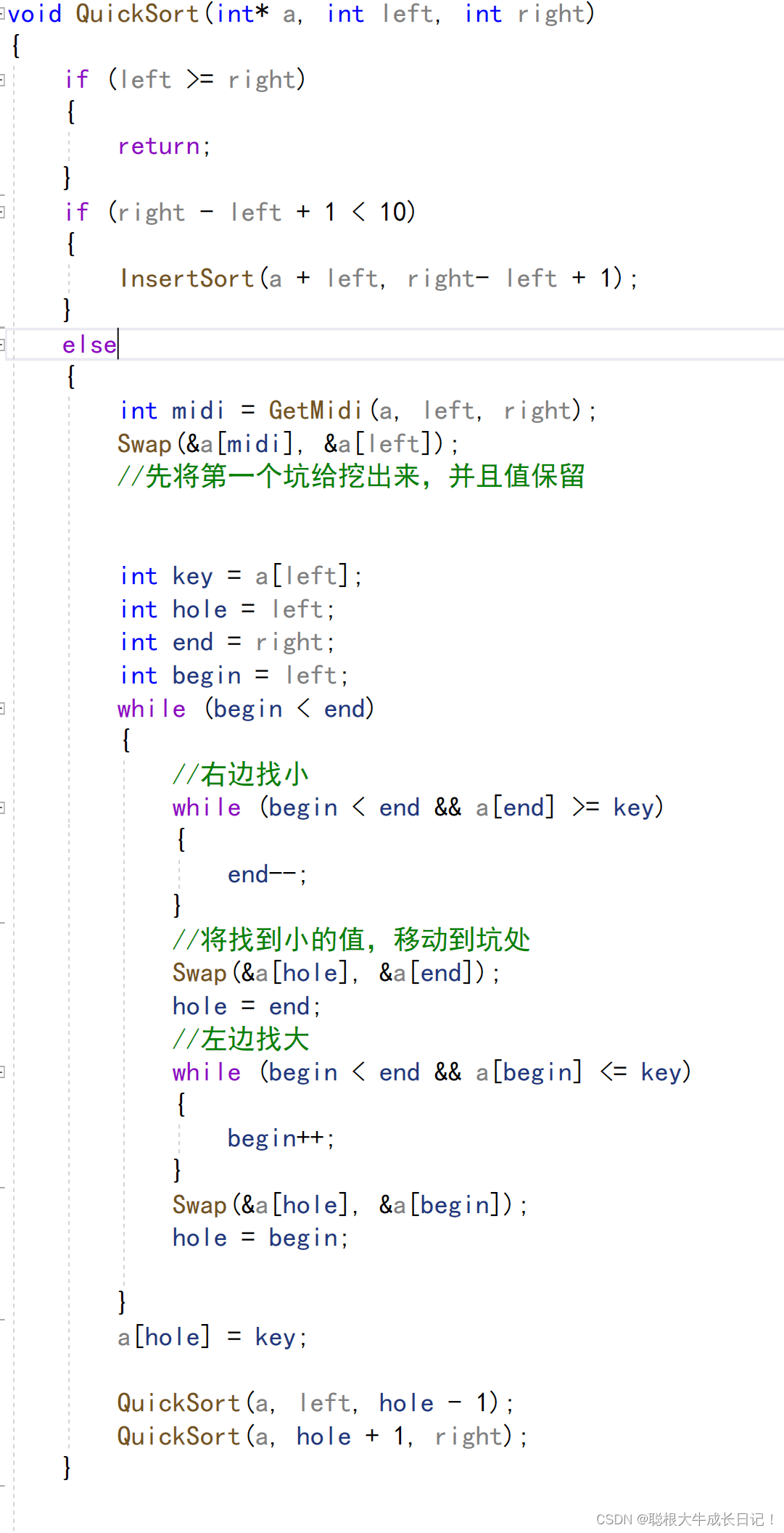
就将这条语句放入QuickSort中就行了
if (right - left + 1 < 10)
	{
		InsertSort(a + left, right- left + 1);
	}

到这里我们的快速排序就基本上手撕完毕了，感谢大家的观看，如果你觉得对你有用的话，可以点个赞哦！！