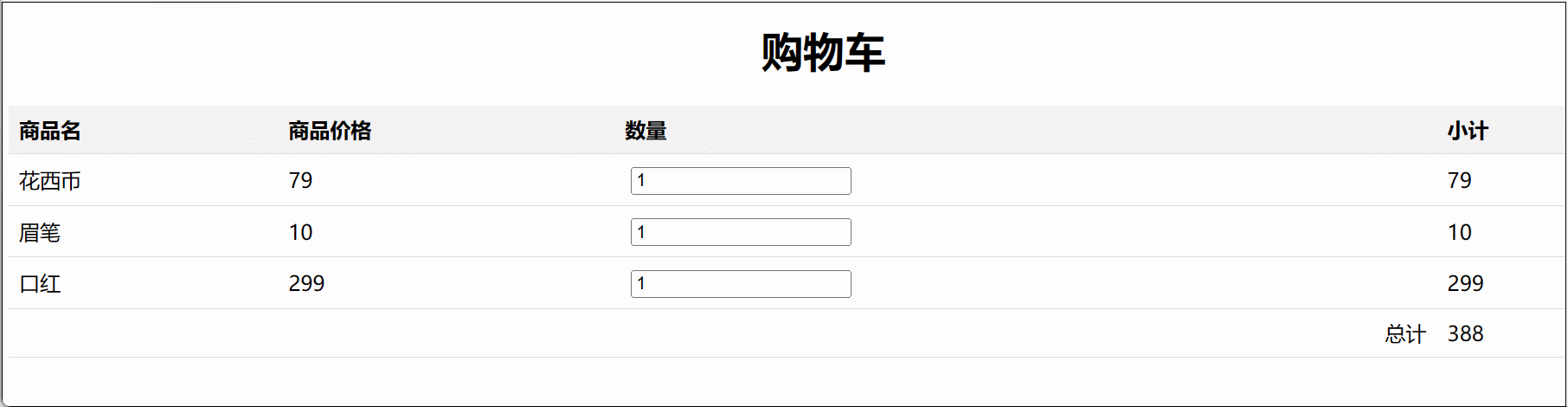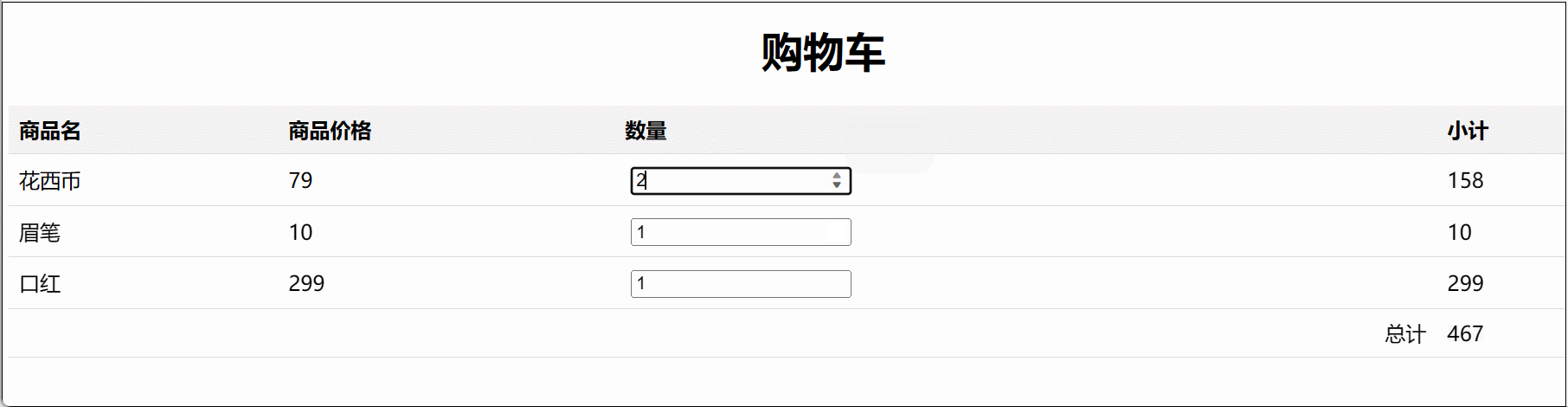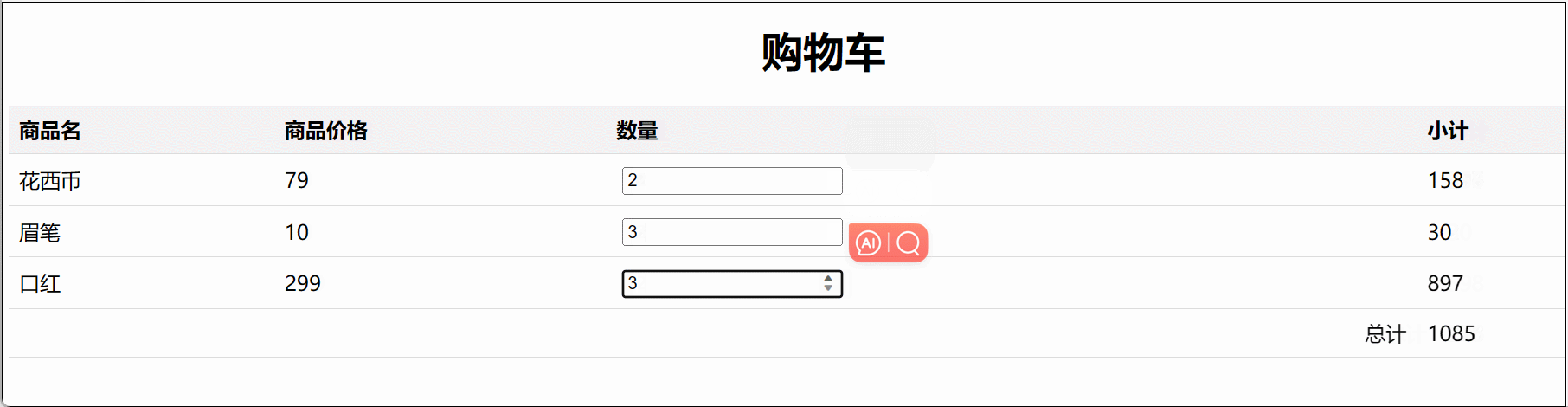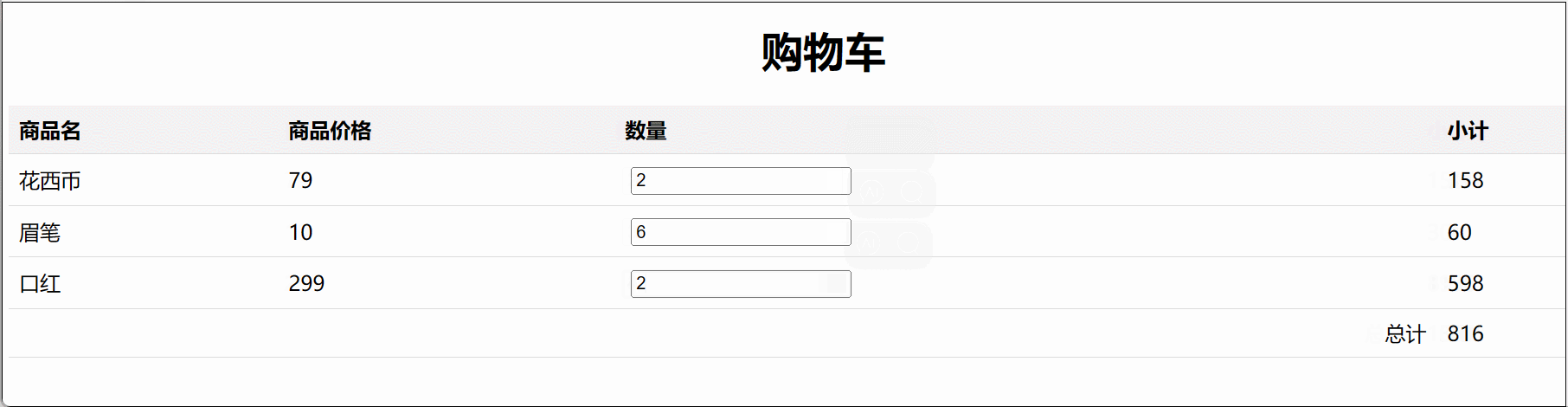
1.背包问题
1.1.01背包问题
01背包问题是在M件物品中选择若干件放在空间为W的背包中,每件物品的体积为W1,W2至Wn,价值为P1,P2至Pn,01背包的约束条件是给定几种物品,每种物品有且只有一个,并且有权值和体积两个属性。
01背包问题常常采用动态规划的方法去求解,状态转移方程为:F(W,i)=max{F(W,i-1),F(W-Wi,i)},表示前i种物品装进容量为W的背包里面获取的最大价值。
2.01背包问题:
有N件物品和一个容器是V的背包。每件物品只能使用一次。
第i件物品的体积vi,价值wi。
求解将哪些物品加入背包,使得总价值最大。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
scanf("%d%d", &v[i], &w[i]);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j--)
f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
cout << f[n][m] << endl;
return 0;
}一维数组形式:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
scanf("%d%d", &v[i], &w[i]);
for(int i = 1;i <= n; i++)
for(int j = m;j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}1.2.完全背包问题
完全背包问题是指有N件物品和一个容量为V的背包,第i件物品的重量为weight[i],价值为value[i],每件物品有无限个,求怎样可以使背包物品价值总量最大。
完全背包问题与01背包问题大致相同,唯一不同的地方体现在遍历顺序方面,倒序遍历可避免一件物品重复选取。
3.完全背包问题
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
scanf("%d%d", &v[i], &w[i]);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
for(int k = 0;k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
return 0;
}但是上面的代码很容易就超时,时间复杂度比较大。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
scanf("%d%d", &v[i], &w[i]);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}改成一维数组形式:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
scanf("%d%d", &v[i], &w[i]);
for(int i = 1;i <= n; i++)
for(int j = v[i];j <= m; j++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}1.3.多重背包问题
多重背包问题是在M种物品中选择若干件放在容量为W的背包中,每种物品有无限多个,01背包的约束条件是给定几种物品,每种物品有且只有一个,并且有权值和体积两个属性。
4.多重背包问题I
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。
多重背包的暴力解法:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
scanf("%d%d%d", &v[i], &w[i], &s[i]);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
for(int k = 0;k <= s[i] && k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
printf("%d\n", f[n][m]);
return 0;}
5.多重背包问题II
有N种物品和一个容器是V的背包
第i种物品最多有s件,每件体积是vi,价值是wi。
求解将哪些物品装入背包,可以使得物品总体积和不超过背包的容量,且价值总和最大。
数据范围:增加到2000
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 25000;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
scanf("%d%d", &n, &m);
int cnt = 0;
for(int i = 1;i <= n; i++)
{
int a, b, s;
scanf("%d%d%d", &a, &b, &s);
int k = 1;
while(k <= s)
{
cnt++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if(s > 0)
{
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for(int i = 1;i <= n; i++)
for(int j = m;j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}9.分组背包问题
有 NN 组物品和一个容量是 VV 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。 每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
{
scanf("%d", &s[i]);
for(int j = 0;j < s[i]; j++)
scanf("%d%d", &v[i][j], &w[i][j]);
}
for(int i = 1;i <= n; i++)
for(int j = m;j >= 0; j--)
for(int k = 0;k < s[i]; k++)
if(v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}2.线性DP
898.数字三角形
给定一个数字三角形,从顶部出发,在每一个结点可以选择移动至其左下方或者右下方的结点,一直走到底层,要求找出一条路径,是路径上的数字之和最大。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 510, INF = 1e9;
int n;
int a[N][N];
int f[N][N];
int main()
{
scanf("%d", &n);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= i; j++)
scanf("%d", a[N][N]);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= i; j++)
f[i][j] = -INF;
f[i][j] = a[1][1];
for(int i = 2;i <= n; i++)
for(int j = 1;j <= i; j++)
f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
int res = -INF;
for(int i = 1;i <= n; i++)
res = max(res, f[n][i]);
printf("%d\n", res);
return 0;
}895.最长上升序列I:
给定一个长度为N,求数值严格单调递增的子序列的长度最长是多少。
状态表示f[i] 集合:所有以第i个数结尾的上升子序列。属性:Max所有的上升子序列
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
scanf("%d", &n);
for(int i = 1;i <= n; i++)
scanf("%d", &a[i]);
for(int i = 1;i <= n; i++)
{
f[i] = 1;//只有a[i]一个数
f(int j = 1;j < i; j++)
if(a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for(int i = 1;i <= n; i++)
res = max(res, f[i]);
printf("%d\n", res);
return 0;
}将要输出的序列打印出来:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N], g[N];
int main()
{
scanf("%d", &n);
for(int i = 1;i <= n; i++)
scanf("%d", &a[i]);
for(int i = 1;i <= n; i++)
{
f[i] = 1;
g[i] = 0;
for(int j = 1;j < i; j++)
if(a[j] < a[j])
{
f[i] = f[j] + 1;
g[i] = j;
}
}
int k = 1;
for(int i = 1;i <= n; i++)
if(f[k] < f[i])
k = 1;
printf("%d\n", f[k]);
for(int i = 0, len = f[k];i < len; i++)
{
printf("%d ", a[k]);
k = g[k];
}
return 0;
}896.最长上升子序列II
数据范围扩展到100000
897.最长公共子序列:
第一个序列的前i个字母,和第二个序列前j个字母构成的子序列比较
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
scanf("%s%s", a+1, b+1);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
printf("%d\n", f[n][m]);
return 0;
}899.编辑距离
给定个长度不超过10的字符串以及次询问,每次询问给出一个字符串和一个操作次数上限。
对于每次询问,请你求出给定的个字符串中有多少个字符串可以在上限操作次数内经过操作变成询问给出的字符串。
每个对字符串进行的单个字符的插入、删除或替换算作一次操作。
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
return 0;
}
3.区间DP
282.石子合并:
设有 NN 堆石子排成一排,其编号为 1,2,3,…,N1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 NN 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2堆,代价为 4,得到 4 5 2, 又合并 1、2 堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=24;
如果第二步是先合并 2、3 堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 310;
int n;
int s[N];
int f[N][N];
int main()
{
scanf("%d", &n);
for(int i = 1;i <= n; i++)
scanf("%d", &s[i]);
for(int i = 1;i <= n; i++)
s[i] += s[i - 1];
for(int len = 2;len <= n; len++)
for(int i = 1;i + len - 1 <= n; i++)
{
int l = i, r = len + i - 1;
f[l][r] = 1e8;
for(int k = l;k < r; k++)
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
printf("%d\n", f[1][n]);
return 0;
}4.计数类DP
敬请期待
5.数位统计DP
338.计数问题
给定两个整数 a和 b,求 a 和 b 之间的所有数字中 0∼9的出现次数。
分别求出1的每一位上出现的次数
#include <bits/stdc++.h>
using namespace std;
int num[10];
int power10(int k)
{
int res = 1;
while(k){
res *= 10;
k --;
}
return res;
}
int getnum(int num[],int x,int y)
{
int res = 0;
for(int i = x;i <= y;i ++){
res = res * 10 + num[i];
}
return res;
}
int solve(int n,int x)//求1~n中x的出现次数
{
if(n == 0) return 0;
int tmp = n,p = 0,res = 0,t;
while(tmp){//获取数字n的每一位
p ++;
tmp /= 10;
}
tmp = n,t = p;
while(tmp){//获取数字n的每一位
num[t --] = tmp % 10;
tmp /= 10;
}
for(int i = 1;i <= p;i ++){//求x在第i位中的出现次数
if(x == 0 && i != 1){//0不可能在第一位出现
res = res + (getnum(num,1,i - 1) - 1) * power10(p - i);
if(num[i] < 1) res = res + getnum(num,i + 1,p) + 1;
else res += power10(p - i);
}
else if(x != 0){
res = res + getnum(num,1,i - 1) * power10(p - i);
if(num[i] == x) res += getnum(num,i + 1,p) + 1;
else if(num[i] > x) res += power10(p - i);
}
}
return res;
}
int main()
{
int a,b;
while(cin >> a >> b,a || b){
if(a > b) swap(a,b);
int ans1[10] = {0},ans2[10] = {0};
for(int i = 0;i < 10;i ++){
int t1 = solve(b,i),t2 = solve(max(a - 1,1),i);
if(a == 1) t2 = 0;
cout << t1 - t2 << ' ';
}
cout << '\n';
}
return 0;
}6.状态压缩DP
291.蒙德里安的梦想
求把 N×M 的棋盘分割成若干个 1×2 的长方形,有多少种方案。
例如当 N=2,M=4 时,共有 5 种方案。当 N=2,M=3 时,共有 3 种方案。
如下图所示:
![]()
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 12, M = 1 << N;
int n, m;
long long f[N][M];
bool st[M];
int main()
{
while(cin >> n >> m, n || m)
{
memset(f, 0, sizeof(f));
for(int i = 0;i < 1 << n; i++)
{
st[i] = true;
int cnt = 0;
for(int j = 0;j < n; j++)
if(i >> j & 1)
{
if(cnt & 1) st[i] = false;
cnt = 0;
}
else cnt++;
if(cnt & 1) st[i] = false;
}
f[0][0] = 1;
for(int i = 1;i <= m; i++)
for(int j = 0;j < 1 << n; j++)
for(int k = 0;k < 1 << n; k++)
if((j & k) == 0 && st[j | k])
f[i][j] += f[i - 1][k];
cout << f[m][0] << endl;
}
return 0;
}91. 最短Hamilton路径
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
#include<iostream>
#include<algorithm>
#icnlude<cstring>
using namespace std;
const int N = 20, M = 1 << N;
int n;
int w[N][N];
int f[M][N];
int main()
{
cin >> n;
for(int i = 0;i < n; i++)
for(int j = 0;j < n; j++)
cin >> w[i][j];
memset(f, 0x3f, sizeof(f));
f[1][0] = 0;
for(int i = 0;i < 1 << n; i++)
for(int j = 0;j < n; j++)
if(i >> j & 1)
for(int k = 0;k < n; k++)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n) - 1][n - 1] << endl;
return 0;
}7.树形DP
285.没有上司的舞会
Ural 大学有 N 名职员,编号为 1∼N。
他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。
每个职员有一个快乐指数,用整数 Hi 给出,其中 1≤i≤N。
现在要召开一场周年庆宴会,不过,没有职员愿意和直接上司一起参会。
在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值。
状态表示:集合所有从以u为根的子树中选择,并且不选u这个点的方案
所有从以u为根的子树中选,并且选择u这个点的方案
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 6010;
int n;
int happy[N];
int h[N], e[N], ne[N], idx;
int f[N][2];
bool has_father[N];
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
f[u][1] = happy[u];
for(int i = h[u];i != -1; i = ne[i])
{
int j = e[i];
dfs(j);
f[u][0] += max(f[j][0], f[j][1]);
f[u][1] += f[j][0];
}
}
int main()
{
scanf("%d", &n);
for(int i = 1;i <= n; i++) scanf("%d", &happy[i]);
memset(h, -1, sizeof(h));
for(int i = 0;i < n - 1; i++)
{
int a, b;
scanf("%d%d", &a, &b);
has_father[a] = true;
add(b, a);
}
int root = 1;
while(has_father[root]) root++;
dfs(root);
printf("%d\n", max(f[root][0], f[root][1]));
return 0;
}8.记忆化搜索
记忆化搜索是一种优化搜索算法的方法,通过将搜索过程可视化,可以快速找到目标节点。在记忆化搜索中,首先将搜索过程记录在一个记忆表中,然后在搜索时检查记忆表以寻找目标节点。这种方法可以大大减少搜索时间,特别是在具有大量节点的图中。
记忆化搜索通常用于解决诸如图匹配、最短路径和最小生成树等问题。在实际应用中,记忆化搜索可以通过动态规划、散列和查表等技术实现。
901.滑雪
给定一个R行C列的矩阵,表示一个矩形网格滑雪场。
矩阵中第i行第1列的点表示滑雪场的第i行第j列区域的高度。
一个人从滑雪场中的某个区域内出发,每次可以向上下左右任意一个方向滑动一个单位距离。
当然,一个人能够滑动到某相邻区域的前提是该区域的高度低于自己目前所在区域的高度。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 310;
int n, m;
int h[N][N];
int f[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dp(int x, int y)
{
int &v = f[x][y];
if(v != -1) return v;
v = 1;
for(int i = 0;i < 4; i++)
{
int a = x + dx[i], b = y + dy[i];
if(a >= 1 && a <= n && b >= -1 && b <= m && h[a][b] < h[x][y])
v = max(v, dp(a, b) + 1);
}
return v;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
scanf("%d", &h[i][j]);
memset(f, -1, sizeof(h));
int res = 0;
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
res = max(res, dp(i, j));
printf("%d\n", res);
return 0;
}