多维时序 | MATLAB实现WOA-CNN-BiGRU-Attention多变量时间序列预测（SE注意力机制）

预测效果

基本描述

1.Matlab实现WOA-CNN-BiGRU鲸鱼算法优化卷积双向门控循环单元多变量时间序列预测；
2.运行环境为Matlab2021b；
3…data为数据集，excel数据，输入多个特征，输出单个变量，考虑历史特征的影响，多变量时间序列预测，
main.m为主程序，运行即可,所有文件放在一个文件夹；
4.命令窗口输出R2、MSE、MAE、MAPE和MBE多指标评价；
5.鲸鱼算法优化学习率，隐藏层节点，正则化系数；

模型描述

注意力机制模块：
SEBlock（Squeeze-and-Excitation Block）是一种聚焦于通道维度而提出一种新的结构单元，为模型添加了通道注意力机制，该机制通过添加各个特征通道的重要程度的权重，针对不同的任务增强或者抑制对应的通道，以此来提取有用的特征。该模块的内部操作流程如图，总体分为三步：首先是Squeeze 压缩操作，对空间维度的特征进行压缩，保持特征通道数量不变。融合全局信息即全局池化，并将每个二维特征通道转换为实数。实数计算公式如公式所示。该实数由k个通道得到的特征之和除以空间维度的值而得，空间维数为H*W。其次是Excitation激励操作，它由两层全连接层和Sigmoid函数组成。如公式所示，s为激励操作的输出，σ为激活函数sigmoid，W2和W1分别是两个完全连接层的相应参数，δ是激活函数ReLU，对特征先降维再升维。最后是Reweight操作，对之前的输入特征进行逐通道加权，完成原始特征在各通道上的重新分配。

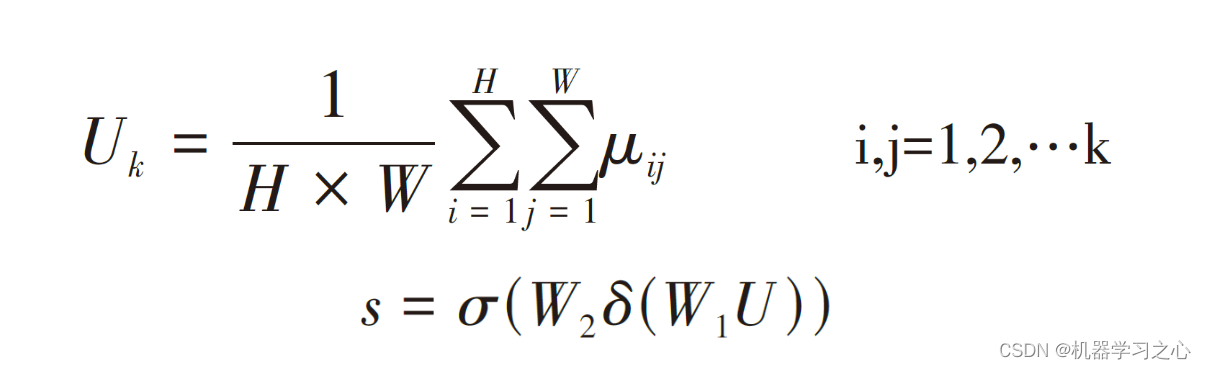
程序设计

• 完整程序和数据获取方式：私信博主回复MATLAB实现WOA-CNN-BiGRU-Attention多变量时间序列预测（SE注意力机制）。

%%  优化算法参数设置
SearchAgents_no = 8;                   % 数量
Max_iteration = 5;                    % 最大迭代次数
dim = 3;                               % 优化参数个数
lb = [1e-3,10 1e-4];                 % 参数取值下界(学习率，隐藏层节点，正则化系数)
ub = [1e-2, 30,1e-1];                 % 参数取值上界(学习率，隐藏层节点，正则化系数)

fitness = @(x)fical(x,num_dim,num_class,p_train,t_train,T_train);

[Best_score,Best_pos,curve]=WOA(SearchAgents_no,Max_iteration,lb ,ub,dim,fitness)
Best_pos(1, 2) = round(Best_pos(1, 2));   
best_hd  = Best_pos(1, 2); % 最佳隐藏层节点数
best_lr= Best_pos(1, 1);% 最佳初始学习率
best_l2 = Best_pos(1, 3);% 最佳L2正则化系数
 
%% 建立模型
lgraph = layerGraph();                                                   % 建立空白网络结构
tempLayers = [
    sequenceInputLayer([num_dim, 1, 1], "Name", "sequence")              % 建立输入层，输入数据结构为[num_dim, 1, 1]
    sequenceFoldingLayer("Name", "seqfold")];                            % 建立序列折叠层
lgraph = addLayers(lgraph, tempLayers);                                  % 将上述网络结构加入空白结构中
tempLayers = [
    convolution2dLayer([3, 1], 16, "Name", "conv_1", "Padding", "same")  % 建立卷积层,卷积核大小[3, 1]，16个特征图
    reluLayer("Name", "relu_1")                                          % Relu 激活层

lgraph = addLayers(lgraph, tempLayers);                                  % 将上述网络结构加入空白结构中

tempLayers = [
    sequenceUnfoldingLayer("Name", "sequnfold")                      % 建立序列反折叠层
    flattenLayer("Name", "flatten")                                  % 网络铺平层
       fullyConnectedLayer(num_class, "Name", "fc")                                      % 分类层
lgraph = addLayers(lgraph, tempLayers);                              % 将上述网络结构加入空白结构中
lgraph = connectLayers(lgraph, "seqfold/out", "conv_1");             % 折叠层输出 连接 卷积层输入
lgraph = connectLayers(lgraph, "seqfold/miniBatchSize", "sequnfold/miniBatchSize"); 
                                                                     % 折叠层输出连接反折叠层输入
lgraph = connectLayers(lgraph, "relu_2", "sequnfold/in");            % 激活层输出 连接 反折叠层输入

%% 参数设置
options = trainingOptions('adam', ...     % Adam 梯度下降算法
    'MaxEpochs', 500,...                 % 最大训练次数 
    'InitialLearnRate', best_lr,...          % 初始学习率为0.001
    'L2Regularization', best_l2,...         % L2正则化参数
    'LearnRateSchedule', 'piecewise',...  % 学习率下降
    'LearnRateDropFactor', 0.1,...        % 学习率下降因子 0.1
    'LearnRateDropPeriod', 400,...        % 经过训练后 学习率为 0.001*0.1
    'Shuffle', 'every-epoch',...          % 每次训练打乱数据集
    'ValidationPatience', Inf,...         % 关闭验证
    'Plots', 'training-progress',...      % 画出曲线
    'Verbose', false);

%% 训练
net = trainNetwork(p_train, t_train, lgraph, options);

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229