【算法与数据结构】JavaScript实现十大排序算法（二）

文章目录

关于排序算法
快速排序
堆排序
计数排序
桶排序
基数排序

关于排序算法

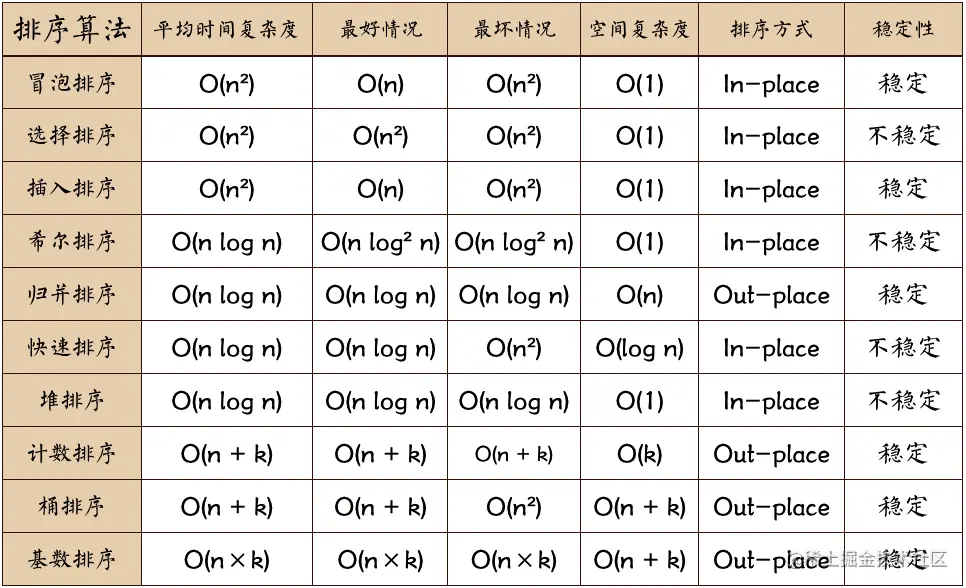
在这里插入图片描述

稳定排序： 在排序过程中具有相同键值的元素，在排序之后仍然保持相对的原始顺序。意思就是说，现在有两个元素a和b，a排在b的前面，且a==b，排序之后a仍然在b的前面，这就是稳定排序。

非稳定排序： 在排序过程中具有相同键值的元素，在排序之后可能会改变它们的相对顺序。意思是说，现在有两个元素a和b，在原始序列中a排在b前面，排序之后a可能会出现在b后面，它们的相对位置可能会发生变化。

原地排序： 在排序过程中不需要申请多余的存储空间，只利用原来存储待排数据的存储空间进行比较和交换的数据排序。这意味着在原地排序中，排序操作会直接修改原始数据，而不需要创建新的数据结构来存储排序后的结果。

非原地排序： 在排序过程中需要申请额外的存储空间来存储临时数据或排序结果，而不直接在原始数据上进行修改。

快速排序

基本思路： 通过选取一个基准元素，将数组分为两个子数组，其中一个子数组的元素都小于基准元素，另一个子数组的元素都大于基准元素。然后对这两个子数组分别进行递归排序，最终将它们合并起来，就得到了有序数组。

操作步骤：

选择一个基准元素（通常是数组中的第一个元素），定义两个空数组（左数组和右数组）；
遍历数组，将小于基准元素的元素放到左边的数组，将大于基准元素的元素放到右边的数组；
对左数组和右数组分别进行递归排序；
将左数组、基准元素、右数组合并起来，得到有序数组。

在这里插入图片描述

例题：

对 a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48] 进行从小到大排序。

  <script>
    function QuickSort(arr) {
      if (arr.length <= 1) return arr
      // 选择第一个元素作为基准元素
      const pivot = arr[0];
      let left = [], right = []
      // 将数组中比基准元素小的元素放到 left 数组，比基准元素大的元素放到 right 数组
      for (let i = 1; i < arr.length; i++) {
        arr[i] < pivot ? left.push(arr[i]) : right.push(arr[i])
      }
      // 递归地对左右两个数组进行快速排序，然后将结果合并在一起，基准元素在中间
      return QuickSort(left).concat(pivot, QuickSort(right))
    }
    let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
    QuickSort(a)
  </script>

总结： 不稳定排序，空间复杂度为O(log n)，时间复杂度为O(nlog n)。

堆排序

基本思路： 利用堆这种数据结构来实现排序操作，堆必须是一个完全二叉树 。
完全二叉树： 除了最底层的叶子节点外，每一层上的节点都有两个子节点（左子节点和右子节点），如果某一层的节点数没有达到最大值，那么这些节点必须从左向右连续存在，不能有空缺。将完全二叉树存储在一维数组中，若节点的下标为i，则左子节点下标为2i+1，右子节点下标为2i+2。

操作步骤：

建堆（Heapify）：将待排序的数组构建成一个二叉堆（通常是最大堆或最小堆）。建堆过程可以从最后一个非叶子节点开始，依次向前对每个节点进行堆调整操作，确保每个子树都满足堆的性质；
排序：建堆完成后，堆顶元素就是最大值或最小值（取决于是最大堆还是最小堆），将堆顶元素与最后一个元素交换，然后将堆的大小减一，再对堆顶元素进行堆调整，使其满足堆的性质。重复这个过程直到堆中只剩一个元素，排序完成。

例题：

对 a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48] 进行从小到大排序。

  <script>
    // 堆排序函数
    function heapSort(arr) {
      // 第一步：建立最大堆
      for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--) {
        heapify(arr, arr.length, i);
      }
      // 第二步：一个个从堆中取出元素，进行排序
      for (let i = arr.length - 1; i > 0; i--) {
        // 将当前最大的元素移到数组末尾
        [arr[0], arr[i]] = [arr[i], arr[0]];
        // 调整剩余元素为最大堆
        heapify(arr, i, 0);
      }
      return arr;
    }
    // 辅助函数：将以 i 为根的子树调整为最大堆
    function heapify(arr, n, i) {
      let largest = i;
      const left = 2 * i + 1;
      const right = 2 * i + 2;
      // 如果左子节点比根节点大，则标记左子节点
      if (left < n && arr[left] > arr[largest]) {
        largest = left;
      }
      // 如果右子节点比根节点大，则标记右子节点
      if (right < n && arr[right] > arr[largest]) {
        largest = right;
      }
      // 如果最大值不是当前节点，则交换它们，并递归调整下面的子树
      if (largest !== i) {
        [arr[i], arr[largest]] = [arr[largest], arr[i]];
        heapify(arr, n, largest);
      }
    }
    // 测试堆排序
    const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
    heapSort(arr);
  </script>

总结： 不稳定排序，原地排序算法，不需要额外的存储空间，空间复杂度为O(1)，时间复杂度为O(nlog n)。
注意： 堆排序的常数因子较大，因此在实际应用中，对于小规模数据或者数据已经近乎有序的情况，可能不如其他排序算法（如快速排序或归并排序）效率高。但对于大规模乱序数据，堆排序通常具有较好的性能。

计数排序

基本思路： 统计每个输入的相同元素的个数，然后根据这些统计信息，将元素放回其在输出数组中的正确位置。

操作步骤：

找到待排序数组中的最大值（max）和最小值（min），确定计数数组的大小范围；
创建一个计数数组（countArray），其大小为max - min + 1，用于统计每个元素在原数组中出现的次数；
遍历待排序数组，统计每个元素的出现次数并存储在计数数组中；
将结果数组返回作为排序结果。

例题：

对 a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48] 进行从小到大排序。

  <script>
    function CountSort(arr) {
      // 找到数组中的最小值和最大值
      let min = Math.min(...arr);
      let max = Math.max(...arr);
      // 创建一个计数数组，初识元素值为0，用于记录每个元素出现的次数
      let countArr = new Array(max + 1).fill(0)
      // 遍历原始数组，统计每个元素出现的次数
      for (let i in arr) {
        countArr[arr[i]]++;
      }
      // 创建一个用于存放排序结果的数组
      let sortArr = []
      // 遍历计数数组，按照顺序将元素添加到排序结果数组中
      for (let i = min; i <= max; i++) {
        if (countArr[i] > 0) {
          sortArr.push(i)
          countArr[i]--
        }
      }
      return sortArr
    }
    const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
    CountSort(arr)
  </script>

总结： 稳定排序，空间复杂度为O(k)【k是非负整数的范围（即最大元素值减去最小元素值加1）】，时间复杂度为O(n+k)【n是排序元素的个数，k是非负整数的范围】。
注意： 计数排序适用于非负整数的排序，如果待排序的元素是浮点数或负数，就不太适合使用计数排序。此外，计数排序在元素范围k较大时，会占用较大的内存空间，因此在元素范围较大的情况下，空间复杂度可能较高。

桶排序

基本思路： 将元素分布均匀到不同的桶中，然后对每个桶中的元素进行排序，最后按照桶的顺序将元素合并。

操作步骤：

确定桶的数量：首先确定要使用的桶的数量，通常桶的数量可以根据元素的范围和数量来确定；
分配元素到桶中：遍历待排序的元素，根据元素的大小将每个元素分配到相应的桶中；
对每个桶进行排序：对每个非空的桶中的元素进行排序，可以使用其他排序算法，例如插入排序或快速排序；
合并桶中的元素：按照桶的顺序，将每个桶中的元素合并成一个有序序列。

在这里插入图片描述

例题：

对 a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48] 进行从小到大排序。

  <script>
    function BucketSort(arr) {
      // 找到数组中的最大值和最小值
      let max = Math.max(...arr)
      let min = Math.min(...arr)
      // 计算桶的数量，创建并初始化桶容器
      let bucketCount = Math.floor((max - min) / arr.length) + 1
      let buckets = new Array(bucketCount)
      for (let i = 0; i < buckets.length; i++) {
        buckets[i] = []
      }
      // 将元素分配到桶中
      for (let i = 0; i < arr.length; i++) {
        const bucketIndex = Math.floor((arr[i] - min) / arr.length)
        buckets[bucketIndex].push(arr[i])
      }
      // 对每个桶中的元素进行排序
      const sortArr = []
      for (let i = 0; i < buckets.length; i++) {
        InsertionSort(buckets[i])
        sortArr.push(...buckets[i])
      }
      return sortArr
    }
    // 插入排序
    function InsertionSort(arr) {
      for (let i = 1; i < arr.length; i++) {
        let temp = arr[i]
        let j;
        for (j = i - 1; j >= 0 && arr[j] > temp; j--) {
          arr[j + 1] = arr[j]
        }
        arr[j + 1] = temp
      }
    }
    const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
    BucketSort(arr)
  </script>

总结： 稳定排序，空间复杂度为O(n+k)【 n 为待排序元素的数量，k 为桶的数量】，时间复杂度为O(n+k)【 n 为待排序元素的数量，k 为桶的数量】。
注意： 桶排序要求元素必须均匀分布在不同的桶中，否则可能导致不均匀的桶大小，影响排序性能。

基数排序

基本思路： 将所有元素统一为相同位数长度，位数长度不足的进行补零。接着从最低位开始，将每位相同的放到同一个容器里，依次进行排序。然后从最低位一直到最高位按照上述操作进行排序，就能得到有序序列。

操作步骤：

确定待排序的整数范围（通常是最小值和最大值）；
根据范围确定需要的容器数量；
将待排序的整数按照个位、十位、百位等位数进行分配到相应的容器中（这里可以使用计数排序作为每个位数上的排序算法）；
按照容器的顺序依次收集每个容器中的元素，形成新的待排序序列；
重复步骤3和步骤4，直到对所有位数都进行了排序。

例题：

对 a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48] 进行从小到大排序。

在这里插入图片描述

  <script>
    function RadixSort(arr) {
      // 获取数组中的最大值
      let max = Math.max(...arr)
      let maxDigit = getMaxDigits(max)
      for (let i = 0; i < maxDigit; i++) {
        // 创建并初始化容器
        const buckets = Array.from({ length: 10 }, () => [])
        for (let j = 0; j < arr.length; j++) {
          const digit = getDigit(arr[j], i)
          buckets[digit].push(arr[j])
        }
        arr = [].concat(...buckets)
      }
      return arr
    }
    // 获取数组中最大位数
    function getMaxDigits(max) {
      let digit = 0
      while (max > 0) {
        max = Math.floor(max / 10)
        digit++
      }
      return digit
    }
    // 获取元素的某位数上的数字
    function getDigit(num, place) {
      return Math.floor(Math.abs(num) / Math.pow(10, place)) % 10;
    }
    let arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
    let a = RadixSort(arr)
    console.log(a);
  </script>