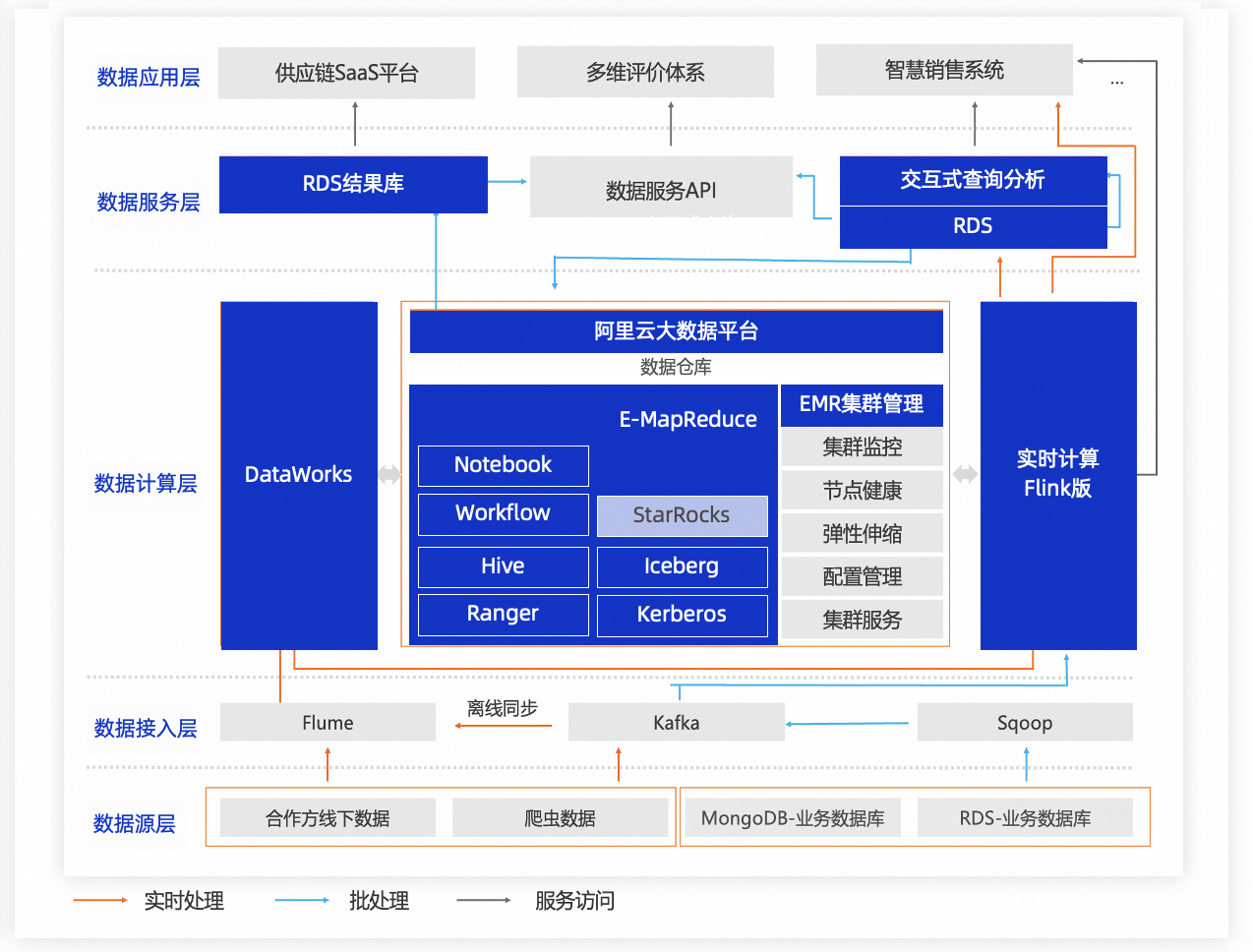
B - 树是一种自平衡的多路搜索树,能够有效地存储和检索数据,被广泛应用于文件系统、数据库等领域。以下是 B - 树的实现原理:
定义及性质:
- 定义:B - 树是一种平衡的多路查找树,它在查找、插入和删除操作上具有较高的效率。
- 性质:
- 每个节点最多有 m 个子节点,最少有「[m/2]个子节点,其中 m 称为 B-树的阶。
- 除根节点外,每个节点至少有[m/2]-1 个关键字,根节点至少有1个关键字。
C - 节点内的关键字是有序排列的,对于任意非叶子节点,其关键字 k; 满足 k < k₂ <・·< kn-1,n 为节点内关键字的个数。
- 每个关键字 k; 对应一个子节点指针 p,且指针 " 所指向的子节点中的所有关键字都小于 ki+1。
数据结构:
- 通常使用数组或链表来实现 B - 树的节点。每个节点包含以下信息:
- 一个关键字数组,用于存储节点中的关键字。
- 一个子节点指针数组,用于指向该节点的子节点。
- 一个记录当前节点中关键字个数的变量。
查找操作:
- 从根节点开始,将待查找的关键字与当前节点中的关键字进行比较。
- 如果待查找的关键字等于当前节点中的某个关键字,则查找成功。
- 如果待查找的关键字小于当前节点中的某个关键字,则沿着该关键字对应的子节点指针继续查找。
- 如果待查找的关键字大于当前节点中的所有关键字,则沿着最后一个子节点指针继续查找。
- 重复上述步骤,直到找到关键字或到达叶子节点。如果到达叶子节点仍未找到关键字,则查找失败。
插入操作:
首先通过查找操作确定待插入关键字的位置
说明该关键字已存在,插入操作失败。
如果香找成功,
如果查找失败,根据查找路径确定要插入的叶子节点。
如果插入后叶子节点的关键字个数未超过 m-1,则直接将关键字插入到叶子节点的适当位置,并保持关
键字的有序性。
如果插入后叶子节点的关键字个数超过了 m - 1,则需要对该节点进行分裂操作。将节点中间的关键字提
升到父节点,左右两部分关键字分别作为两个新的子节点,并调整父节点及更高层节点的指针和关键字
删除操作:
首先通过查找操作找到要删除的关键字所在的节点。
如果该关键字所在节点为叶子节点,且删除后节点的关键字个数不小于m/2]-1,则直接删除该关键
关
如果该关键字所在节点为叶子节点,且删除后节点的关键字个数小于[m/2]- 1,则需要进行调整操作
如向兄弟节点借关键字或与兄弟节点合并等,以保证节点的关键字个数满足 B-树的性质。
如果要删除的关键字所在节点为非叶子节点,则用该节点的前驱或后继关键字替换要删除的关键字,然后
在相应的叶子节点中删除替换后的关键字,后续的处理与删除叶子节点中的关键字类似。
示例:
下面以一个简单的 3 阶 B - 树为例,展示 B - 树的操作过程。
初始的 B - 树为空,插入关键字10 ,此时 B - 树只有一个节点,如下:
10继续插入关键字 20、30,插入后的 B - 树为:
20
/ \
10 30 插入关键字 40,此时根节点已满,需要进行分裂操作,将 20 提升到新的根节点,左右两部分分 别为 10 和
30,40,得到的 B-树如下:
20
/ \
10 30
/
40插入关键字 50,插入后的 B-树为:
20
/ \
10 30
/ \
40 50删除关键字 30,由于 30 所在节点为非叶子节点,用其前驱关键字 20 替换 30,然后在叶子节点中删除 20
得到的 B-树如下:
20
/ \
10 40
/
50B - 树通过其特殊的结构和相应的操作算法,能够在动态变化的数据集合中保持较好的平衡性,从而保证了查找、插入和删除操作的高效性。
与其他数据结构的比较
- 与二叉查找树比较:二叉查找树每个节点只有两个子节点,而 B - 树是多路分支,在相同数量的关键字情况下,B - 树的高度相对较低,查找、插入和删除操作的平均时间复杂度更优,尤其是在数据量较大时,B - 树的优势更加明显。
- 与哈希表比较:哈希表的查找操作在理想情况下时间复杂度为 ,但哈希表不支持范围查询,且在处理动态数据时可能会出现哈希冲突等问题。而 B - 树支持范围查询,且在数据动态变化时能够较好地保持平衡,性能相对稳定。
B - 树通过其独特的结构和高效的操作算法,在数据存储和检索方面具有显著优势,是许多系统中用于优化数据访问性能的重要数据结构之一 。
应用场景
- 数据库系统:B - 树常用于数据库的索引结构,如 MySQL 中的 InnoDB 存储引擎就使用了 B + 树(B - 树的一种变体)来实现索引,能够快速定位和访问数据,提高查询效率。
- 文件系统:在文件系统中,B - 树可用于管理文件和目录的索引,加快文件查找和访问速度。
- 操作系统:操作系统中的虚拟内存管理也可能会用到 B - 树,用于管理内存页的索引等。