>>往期文章：

解决0-1背包问题（方案一）:二维dp数组_呵呵哒(￣▽￣)"的博客-CSDN博客

解决0-1背包问题（方案二）：一维dp数组（滚动数组）_呵呵哒(￣▽￣)"的博客-CSDN博客

LeetCode 416.分割等和子集（动态规划【0-1背包问题】采用一维数组dp:滚动数组）

416. 分割等和子集 - 力扣（LeetCode）

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

解题思路来自代码随想录：代码随想录 (programmercarl.com)

本题要求集合里能否出现总和为 sum / 2 的子集。

看看背包问题如何来解决

只有确定了如下四点，才能把01背包问题套到本题上来。

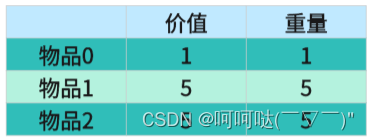
• 背包的体积为sum / 2
• 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
• 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素是不可重复放入。

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        int target = 0;
        for(int i=0;i<nums.size();i++) {
            sum += nums[i];
        }
        if (sum % 2 == 1) return false;
        target = sum / 2;
        // 初始化
        //vector<int> dp(target+1,0);
        vector<int> dp(10001, 0);
        // 遍历
        for(int i=0;i<nums.size();i++) { //遍历物体
            for(int j=target;j>=nums[i];j--) { //遍历背包
                dp[j] = max(dp[j],dp[j-nums[i]] + nums[i]);
            }
        }

        // 返回bool
        if(dp[target] == target) return true;
        return false;
    }
};
// nums = [1,5,11,5] 数组可以分割成 [1, 5, 5] 和 [11] 
// nums = [1,2,3,5] 数组不能分割成两个元素和相等的子集。


// 1 5 11 5 
// {1 5 5}   {11}

// >>分步思考和分析

// 1.求sum
//     1+5+11+5=22
//     sum = 22
// 2.求target = sum / 2
//     22/2=11

// 3.背包问题(O_O)?

// 4.递推公式
// dp[j] = max(dp[j],dp[j-nums[i]] + nums[i]);

// 5.初始化
// dp[0] = 0
// 数组dp可初始化为0

// 6.遍历方式
// 先遍历物体，在从后往前遍历背包
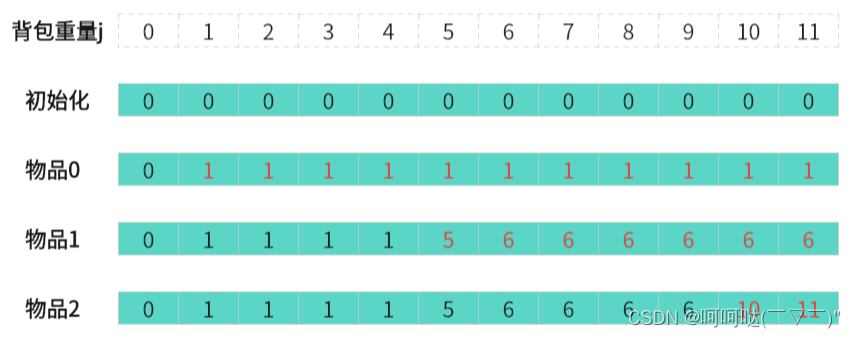
//  0 1 2 3 4 5 6 7 8 9 10 11  j
//  | | | | | | | | | |  | | 
//  --------------------------------
//  0 0 0 0 0 0 0 0 0 0 0  0   初始化
//  0 1 1 1 1 1 1 1 1 1 1  1    价值（max）
//  0 1 1 1 1 5 6 6 6 6 6  6    价值（max）
//  0 1 1 1 1 5 6 6 6 6 6  11   价值（max）
//  0 1 1 1 1 5 6 6 6 6 10 11   价值（max）