本专栏内容为：八大排序汇总 通过本专栏的深入学习，你可以了解并掌握八大排序以及相关的排序算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：八大排序汇总
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

堆排序算法

堆排序就是利用堆(假设利用大顶堆)进行排序的方法。它的基本思想是，将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大值。如此反复执行，便能得到一个有序序列了。

例如下图所示，图1是一个大顶堆，90为最大值，将90与20(末尾元素) 互换，如图2所示，此时90就成了整个堆序列的最后一个元素，将20经过调整，使得除90以外的结点继续满足大顶堆定义(所有结点都大于等于其孩子)，见图3，然后再考虑将30与80互换…

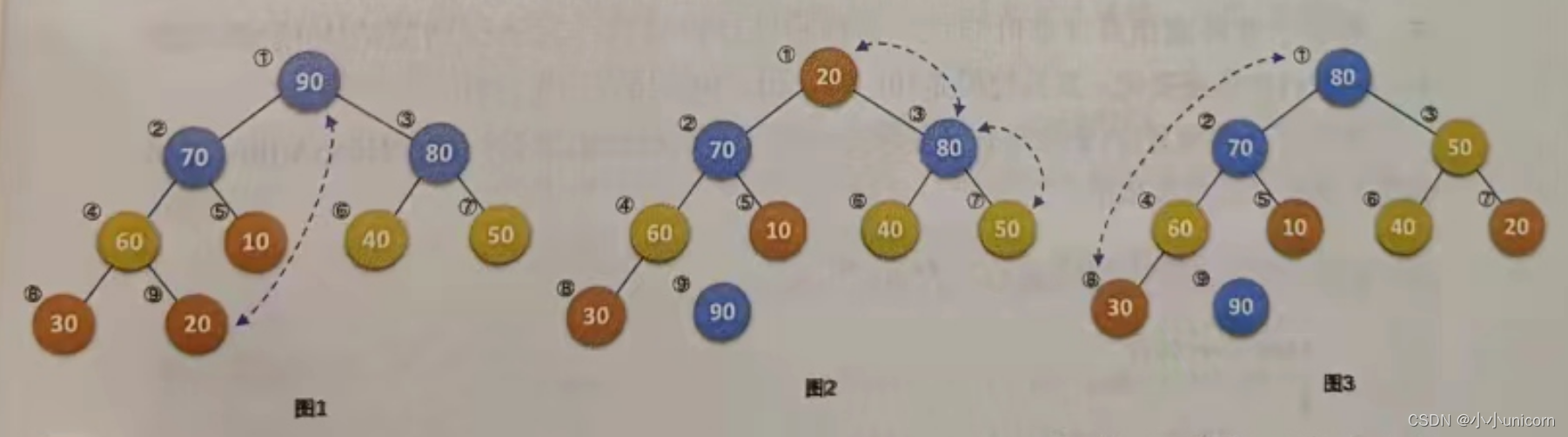
也就是说，我们一开始把排序数据构建成一个大顶堆，然后每次找到一个较大值进行一次排序交换时，要让剩余的数据仍旧满足大顶堆的结构，这就为后面继续排序带来了快捷和高效。相信大家有些明白堆排序的基本思想了，不过要实现它还需要解决两个问题:
(1)如何由一个无序序列构建成一个堆?
(2)如何在输出堆顶元素后，调整剩余元素成为一个新的堆?

要解释清楚它们，让我们来看代码:

注意：排序用到的结构与函数在第一部分：排序的基本概念与分类。我们已经实现。详情请点击：八大排序（一）--------排序的基本概念与分类

void HeapSort(SqList* L)/* 对顺序表L进行堆排序 */
{

    int i;
    for (i = L->length / 2; i > 0; i--)/* 把L中的r构建成一个大顶堆 */
        HeapAdjust(L, i, L->length);
    for (i = L->length; i > 1; i--)
    {
        swap(L, 1, i);/* 将堆顶记录和当前未经排序子序列最后一记录交换 */
        HeapAdjust(L,1,i - 1);/* 将L->r[1..i-1]重新调整为大顶堆 */
    }
}

从代码中也可以看出，整个排序过程分为两个for循环。

第一个循环要完成的就是将现在的待排序序列构建成一个大顶堆。

第二个循环要完成的就是逐步将每个最大值的根结点与末尾元素交换，并且再调整其成为大顶堆。

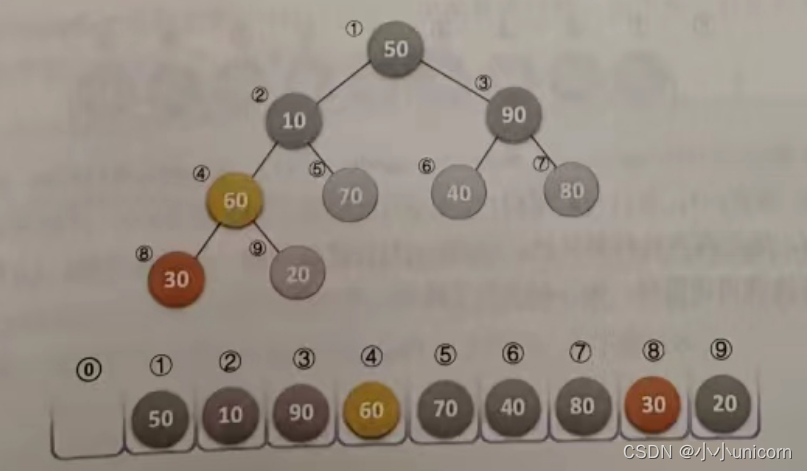
假设我们要排序的序列是{50,10,90,30,70,40,80,60.20}，那么L.length=9，第一个for循环，代码第4行，i是从[9/2]=4开始，4->3->2->1的变量变化。为什么不是从1到9或者从9到1，而是从4到1呢?其实我们看了下图就明白了，它们都有什么规律?它们都是有孩子的结点。注意灰色结点的下标编号就是1、2、3、4。

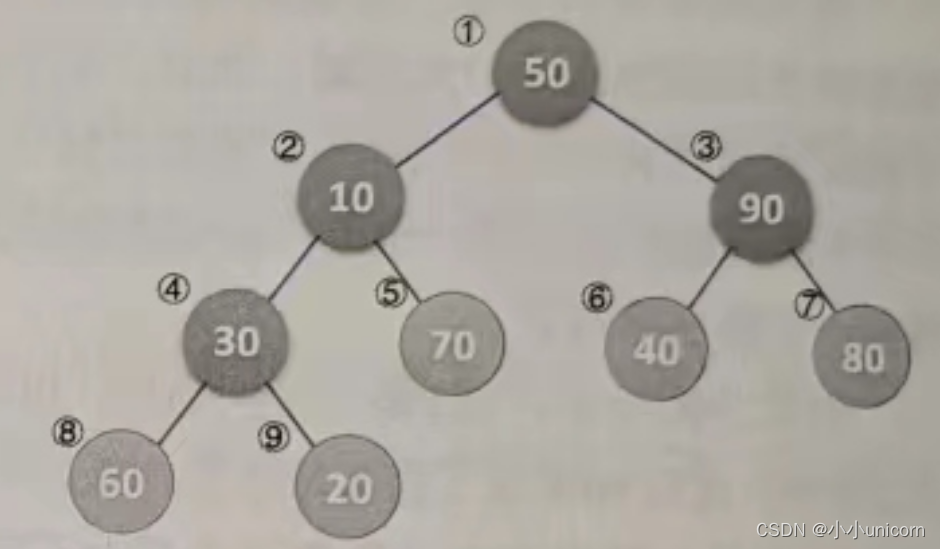
我们所谓的将待排序的序列构建成为一个大顶堆，其实就是从下往上、从右到左，将每个非终端结点(非叶结点)当作根结点，将其和其子树调整成大顶堆。的4->3->2->1的变量变化，其实也就是30，90，10、50的结点调整过程。

既然已经弄清楚i的变化是在调整哪些元素了，现在我们来看关键的HeapAdjust(堆调整)函数是如何实现的。

void HeapAdjust(SqList* L, int s, int m)
{/* 本函数调整L->r[s]的关键字，使L->r[s..m]成为一个大顶堆 */
    int temp, j;
    temp = L->r[s];
    for (j = 2 * s; j <= m; j *= 2)
    {
        if (j < m && L->r[j] < L->r[j + 1])/* 沿关键字较大的孩子结点向下筛选 */
            ++j;/*1为关键字中较大的记录的下标 */
        if (temp >= L->r[j])
            break;/* rc应插入在位置s上 */
        L->r[s] = L->r[j];
        s = j;
    }
    L->r[s] = temp;/* 插入 */
}

(1)函数第一次被调用时，s=4，m=9，传入的SqList参数的值为length=9，r[10]={0,50,10,90,30,70,40,80,60,20}。

(2)第4行，将L.r[s]=L.r[4]=30赋值给temp，如下图所示。

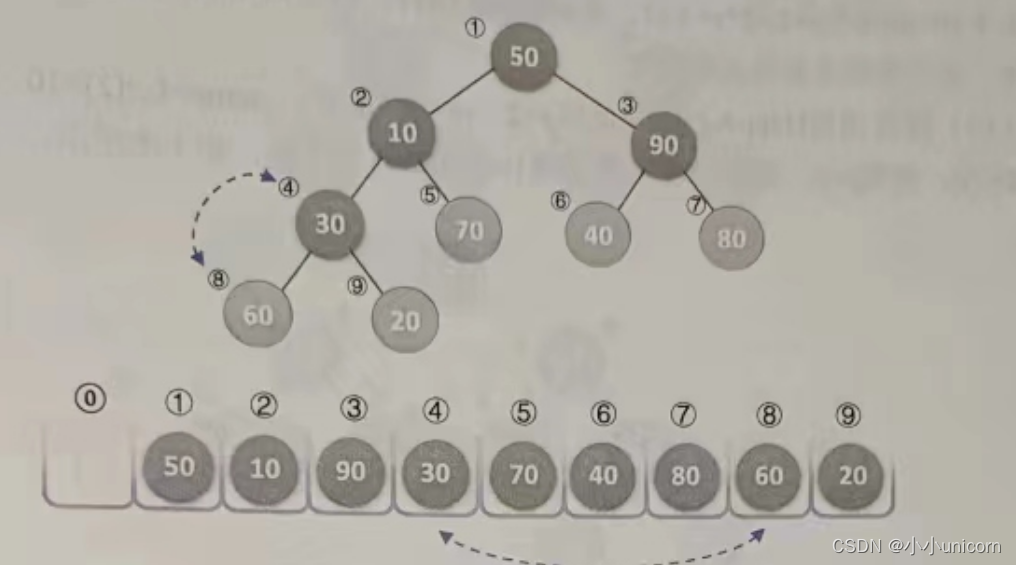
(3)第5~13行，循环遍历其结点的孩子。这里i变量为什么是从2s开始呢?又为什么是j=2递增呢?原因还是二叉树的性质，因为我们这棵是完全二叉树，当前结点序号是s，其左孩子的序号一定是2s，右孩子的序号一定是2s+1，它们的孩子当然也是以2的位数序号增加，因此j变量才是这样循环。

(4)第7行和第8行，此时j=2*4=8，j<m说明它不是最后一个结点，如果L.r[i]<L.r[j+1]，则说明左孩子小于右孩子。我们的目的是要找到较大值，当然需要让j+1以便变成指向右孩子的下标。当前30的左右孩子是60和20，并不满足此条件，因此j还是8。

(5)第9行和第10行，temp=30，L.r[j]=60，并不满足条件。

(6)第11行和第12行，将60赋值给L.r[4]，并令s=j=8。也就是说，当前算出，以30为根结点的子二叉树，当前最大值是60，在第8的位置。注意此时L.r[4]和L.r[8]的值均为60。

(7)再循环因为j=2*j=16，m=9，j>m，因此跳出循环。

(8)第14行，将temp=30赋值给L.r[s]=L.r[8]，完成30与60的交换工作。如下图所示。本次函数调用完成。

(9)再次调用HeapAdjust，此时s=3，m=9。第4行，temp=L.r[3]=90，第7行和第8行，由于40<80得到j+1=2*s+1=7。第9行和第10行，由于90>80，因此退出循环，最终本次调用，整个序列未发什么改变。

(10)再次调用HeapAdjust，此时s=2，m=9。第4行，temp=L.r[2]=10，第7行和第8行，60<70，使得=5。最终本次调用使得10与70进行了互换，如下图所示。

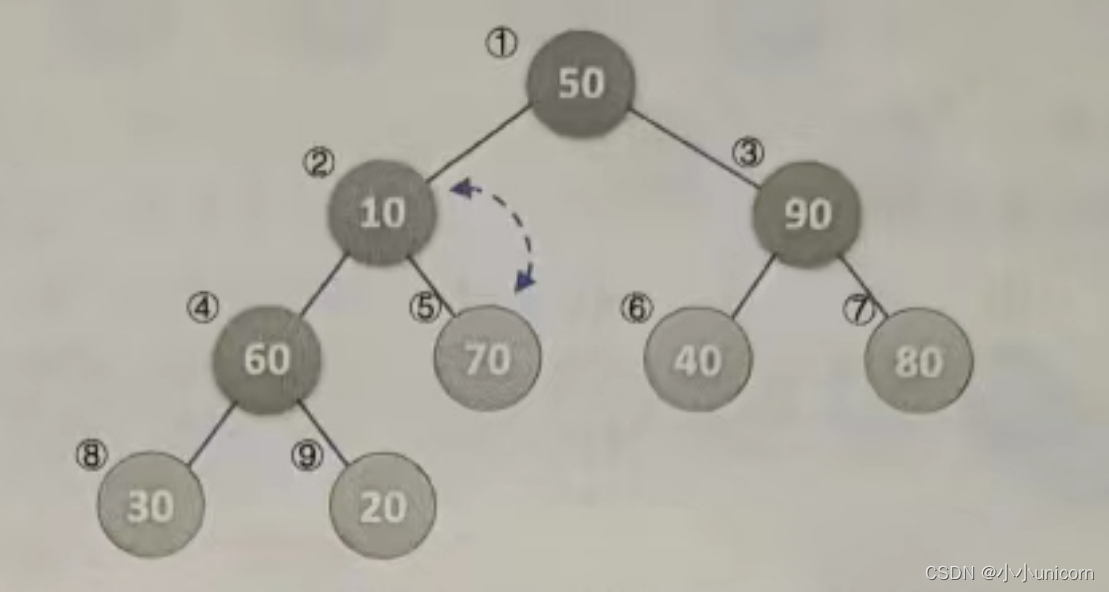
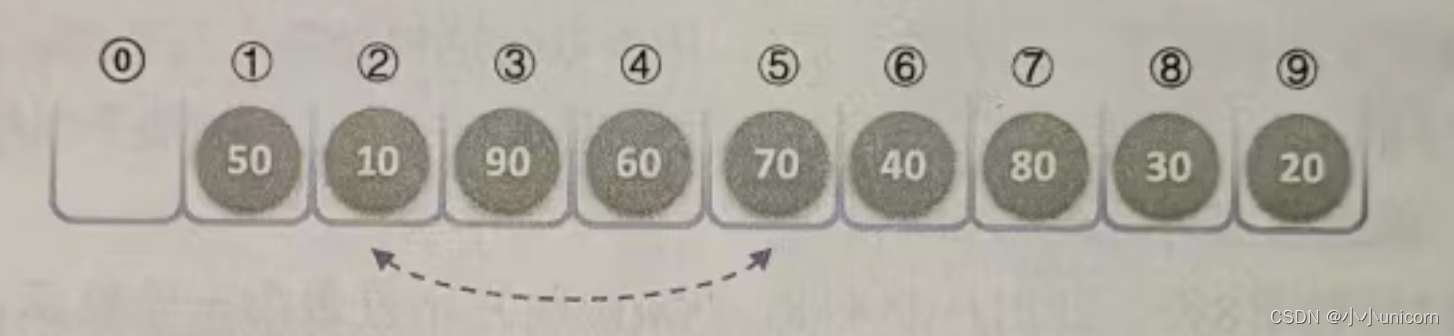
(11)再次调用HeapAdjust，此时s=1，m=9。第4行，temp=L.r[1]=50，第7行和第8行，70<90，使得j=3。第11行和第12行，L.r[1]被赋值了90，并且s=3，再循环，由于2j=6并未大于m，因此再次执行循环体，使得L.r[3]被赋值了80，完成循环后，L.[7]被赋值为50，最终本次调用使得50、90、80进行了轮换，如下图所示。

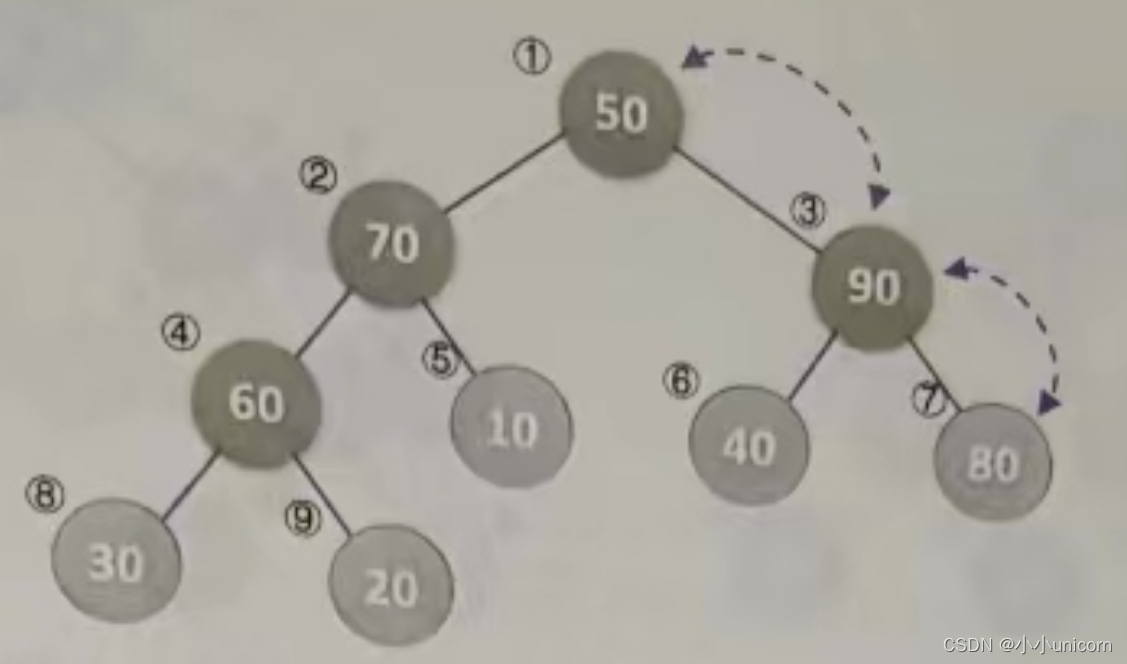
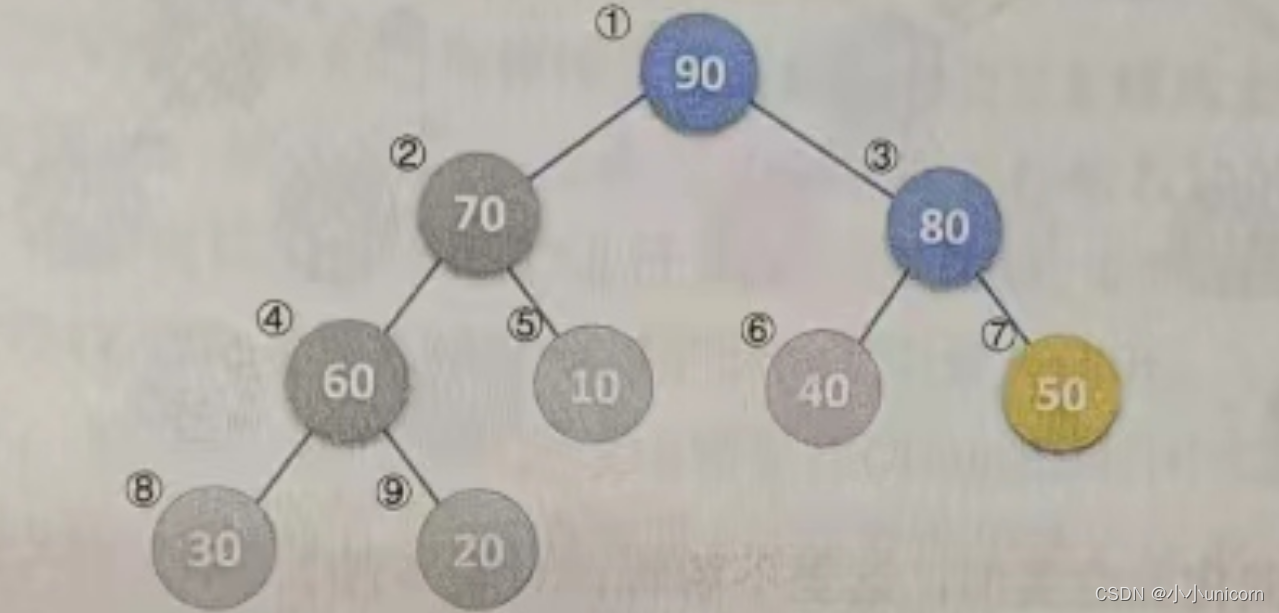
到此为止，我们构建大顶堆的过程算是完成了，也就是HeapSort函数的第4行和第5行循环执行完毕。

或许是有点复杂，如果不明白，多试着模拟计算机执行的方式走几遍，应该就可以理解其原理。接下来HeapSort函数的第6~11行就是正式的排序过程，由于有了前面的充分准备其实这个排序就比较轻松了。下面是这部分代码:

for (i = L->length; i > 1; i--)
    {
        swap(L, 1, i);/* 将堆顶记录和当前未经排序子序列最后一记录交换 */
        HeapAdjust(L,1,i - 1);/* 将L->r[1..i-1]重新调整为大顶堆 */
    }

(1)当i=9时，第8行，交换20与90，第9行，将当前的根结点20进行大顶堆的调整，调整过程和刚才流程一样，找到它左右子结点的较大值，互换，再找到其子结点的较大值互换。此时序列变为{80,70,50,60,10,40,20,30,90}，如下图所示。

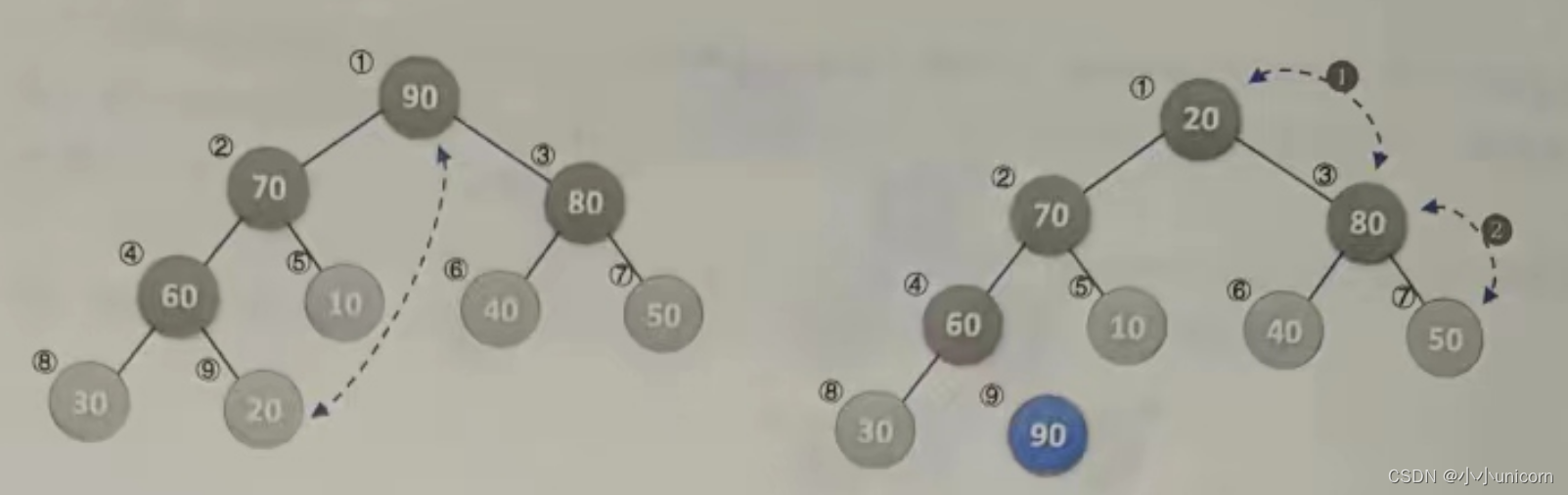
(2)当i=8时，交换30与80，并将30与70交换，再与60交换，此时序列变为{70,60,50,30,10,40,20,80,90}，如下图所示。

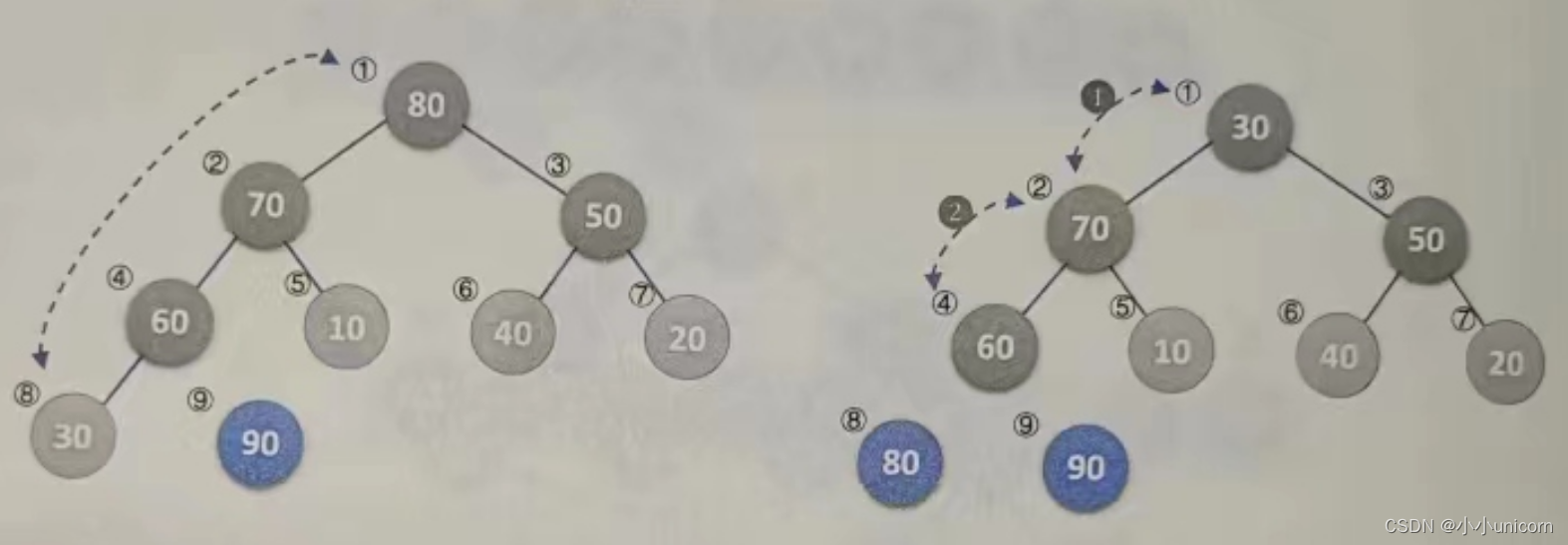
(3)后面的变化完全类似，这里不解释，只看下图。


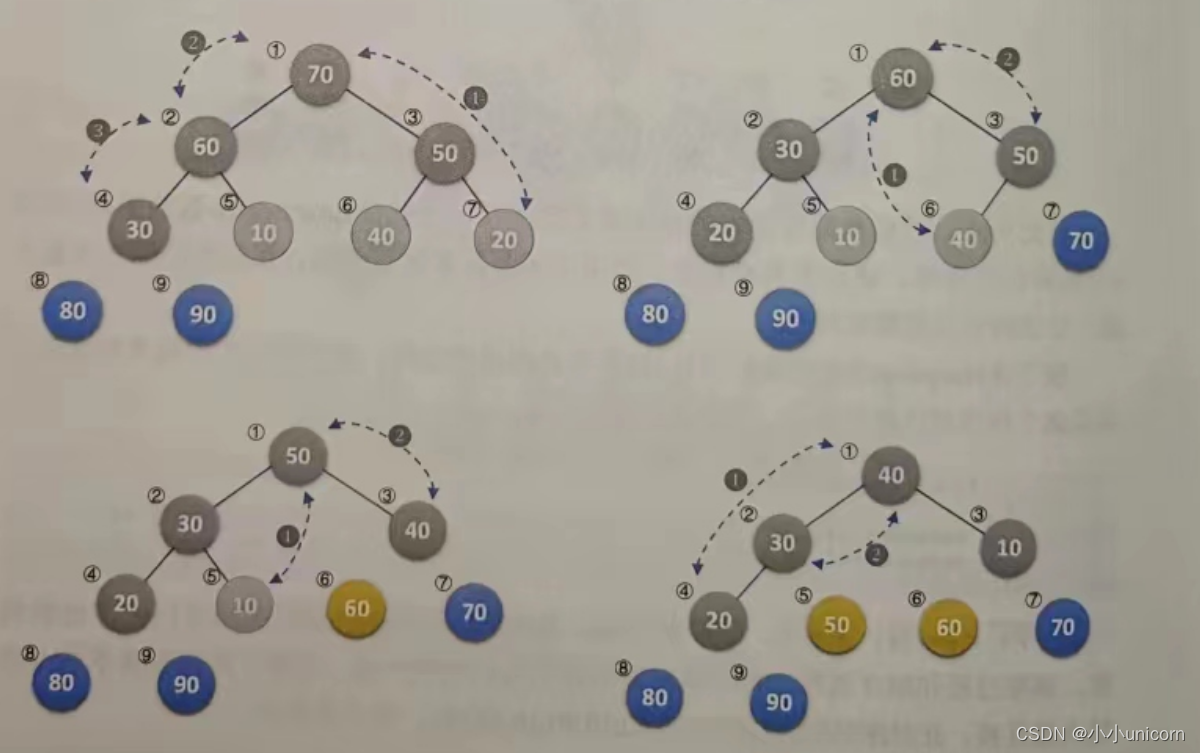
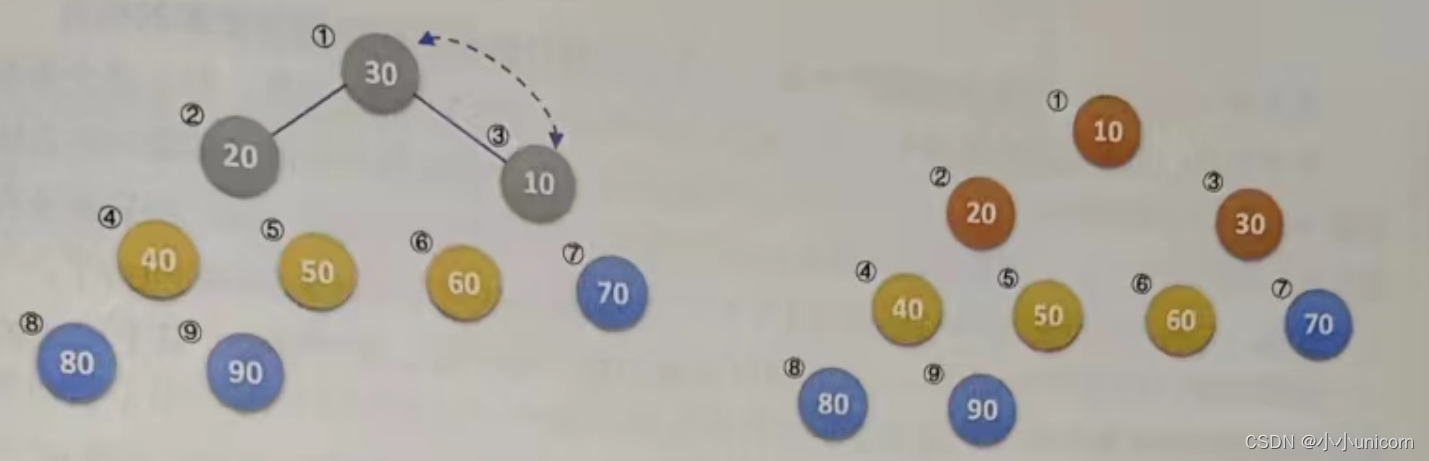
最终就得到一个完全有序的序列了。

堆排序复杂度分析

堆排序的效率到底有多高呢?我们来分析一下。

它的运行时间主要消耗在初始构建堆和在重建堆时的反复筛选上。

在构建堆的过程中，因为我们是完全二叉树从最下层最右边的非终端结点开始构建，将它与其孩子进行比较，若有必要进行互换，对于每个非终端结点来说，其实最多进行两次比较和互换操作，因此整个构建堆的时间复杂度为O(n)。

在正式排序时，第i次取堆顶记录重建堆需要用O(log i)的时间(完全二叉树的某个结点到根结点的距离为([log₂i]+1)，并且需要取n-1次堆顶记录，因此，重建堆的时间复杂度为O(nlogn)。

所以总体来说，堆排序的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感，因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n²)的时间复杂度了。
空间复杂度上，它只有一个用来交换的暂存单元，也非常的不错。不过由于记录的比较与交换是跳跃式进行的，因此堆排序也是一种不稳定的排序方法。

另外，由于初始构建堆所需的比较次数较多，因此，它并不适合待排序序列个数较少的情况。

注意：排序用到的结构与函数在第一部分：排序的基本概念与分类。我们已经实现。详情请点击：八大排序（一）--------排序的基本概念与分类