647. 回文子串

链接: 647. 回文子串
给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：s = “abc”
输出：3
解释：三个回文子串: “a”, “b”, “c”
示例 2：

输入：s = “aaa”
输出：6
解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

解法（动态规划）：
算法思路：
我们可以先「预处理」⼀下，将所有⼦串「是否回⽂」的信息统计在 dp 表⾥⾯，然后直接在表⾥⾯统计 true 的个数即可。

1.状态表示*
为了能表⽰出来所有的⼦串，我们可以创建⼀个 n * n 的⼆维 dp 表，只⽤到「上三⻆部分」
即可。
其中， dp[i][j] 表⽰： s 字符串 [i, j] 的⼦串，是否是回⽂串。

2.状态转移方程
对于回⽂串，我们⼀般分析⼀个「区间两头」的元素：

1. 当 s[i] != s[j] 的时候：不可能是回⽂串， dp[i][j] = 0 ；
2. 当 s[i] == s[j] 的时候：根据⻓度分三种情况讨论：
   • ⻓度为 1 ，也就是 i == j ：此时⼀定是回⽂串，dp[i][j] = true ；
   • ⻓度为 2 ，也就是 i + 1 == j ：此时也⼀定是回⽂串， dp[i][j] =true ；
   • ⻓度⼤于 2 ，此时要去看看 [i + 1, j - 1] 区间的⼦串是否回⽂： dp[i][j]= dp[i + 1][j - 1] 。

综上，状态转移⽅程分情况谈论即可。

3. 初始化
因为我们的状态转移⽅程分析的很细致，因此⽆需初始化。

4. 填表顺序
根据「状态转移⽅程」，我们需要「从下往上」填写每⼀⾏，每⼀⾏的顺序⽆所谓

5. 返回值
根据「状态表⽰和题⽬要求」，我们需要返回 dp 表中 true 的个数

代码：

 int countSubstrings(string s) {
           int n=s.size();

        vector<vector<int>> dp(n,vector<int>(n));
        dp[0][0]=1;
        int sum=1;
        for(int j=1;j<n;j++)
        {
            for(int i=0;i<=j;i++)
            {
                if(s[j]==s[i])
                {
                    if(j==i||j==i+1) dp[i][j]=1;
                    if(j-i>1)
                    {
                        dp[i][j]=dp[i+1][j-1];
                    }
                }
                if(dp[i][j]) sum++;
            }
        }
        return sum;

    }

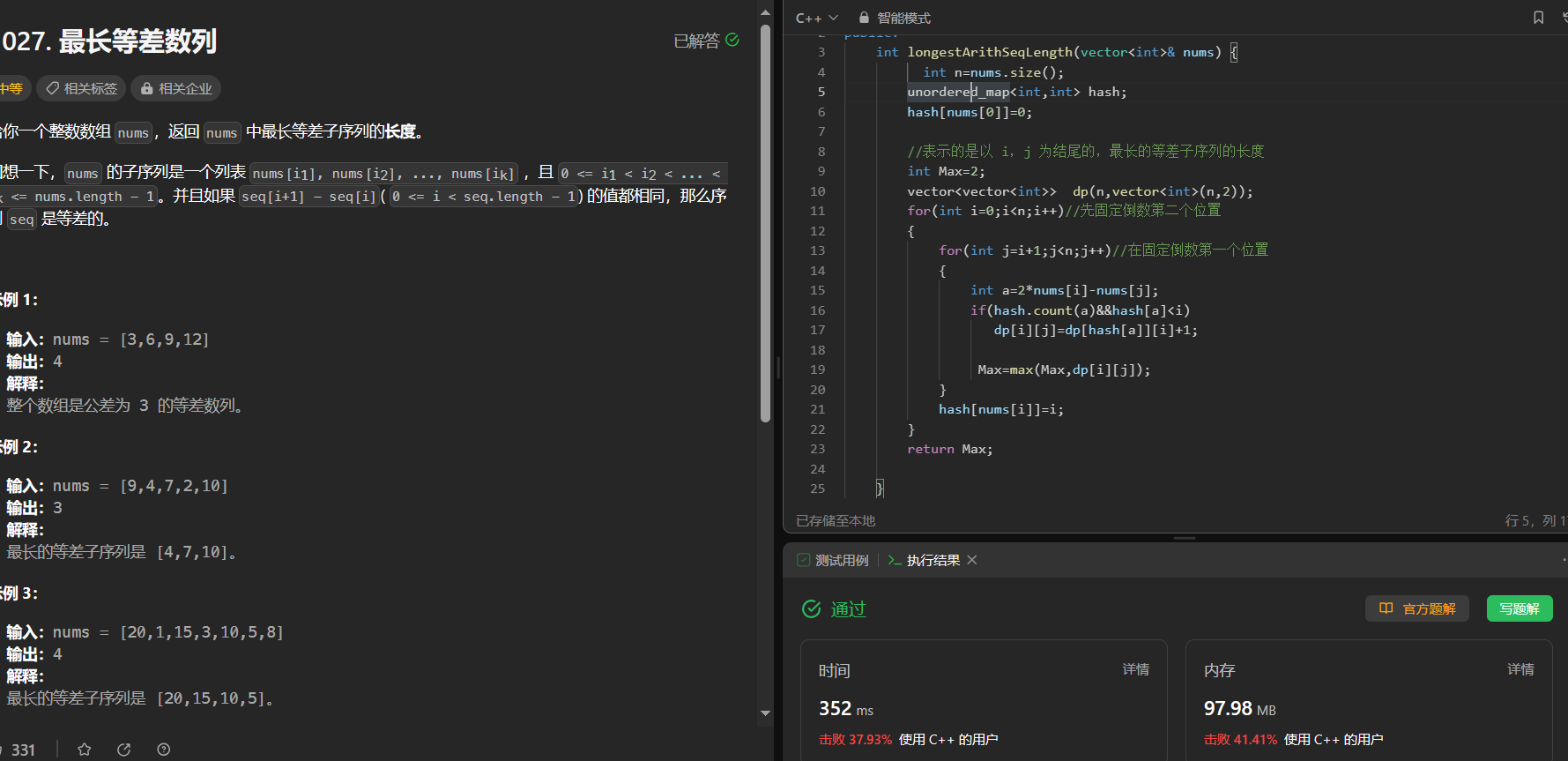
5. 最长回文子串

链接: 5. 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。
示例 2：

输入：s = “cbbd”
输出：“bb”

解法思路：

• a. 我们可以先⽤ dp 表统计出「所有⼦串是否回⽂」的信息
• b. 然后根据 dp 表⽰ true 的位置，得到回⽂串的「起始位置」和「⻓度」。 那么我们就可以在表中找出最⻓回⽂串。

关于「预处理所有⼦串是否回⽂」，已经在上⼀道题⽬⾥已经讲解过了。

代码：

  string longestPalindrome(string s) {
        int n=s.size();

        vector<vector<int>> dp(n,vector<int>(n));
        dp[0][0]=1;
        int sum=1;
        string ret(1,s[0]);
        for(int j=1;j<n;j++)
        {
            for(int i=0;i<=j;i++)
            {
                if(s[j]==s[i])
                {
                    if(j==i||j==i+1) dp[i][j]=1;
                    if(j-i>1)
                    {
                        dp[i][j]=dp[i+1][j-1];
                    }
                }
                if(dp[i][j])
                {
                    if(j-i+1>sum)
                    {
                        sum=j-i+1;
                        string tmp(s.begin()+i,s.begin()+j+1);
                        ret=tmp;
                    }
                }
            }
        }
        return ret;

    }