参考文章：https://arxiv.org/abs/2210.00379

1. 概述

  神经辐射场（NeRF）模型是一种新视图合成方法，它使用体积网格渲染，通过MLP进行隐式神经场景表达，以学习3D场景的几何和照明。
  应用：照片编辑、3D表明提取、人体建模、3D表达和视图合成等。
  特点：模型自监督。对于一个场景，只需要多视图图像及其姿态，而无需3D或深度监督。

2. NeRF模型

  NeRF模型将3D场景表达为用神经网络表示的辐射场。辐射场描述了各点在各视角下的颜色和密度。即$$F(x,\theta ,\varphi )\to (c,\sigma )$$其中$x$为点的3D坐标，$(\theta ,\varphi )$为视线的水平角与俯仰角，$c$表示颜色，$\sigma$表示体积网格密度。该函数使用MLP（记为$F_{\Theta }$）进行近似。$(\theta ,\varphi )$也可表达为3维的单位方向向量$d$。
  该表达需要满足多视图一致性，即$\sigma$（场景的内容）与视角无关，而$c$与坐标和视角均相关。通常来说，会设计两个MLP，第一个MLP输入$x$，输出$\sigma$与高维特征向量$h$：$$\sigma ,h=\text{σ-MLP}(x)$$高维特征向量$h$与视线方向$d$拼接后输入第二个MLP得到$c$：$$c=\text{c-MLP}([h;d])$$由于密度和颜色都完全被MLP表达，因此这种方法被称为隐式场景表达。

3. 新视图合成

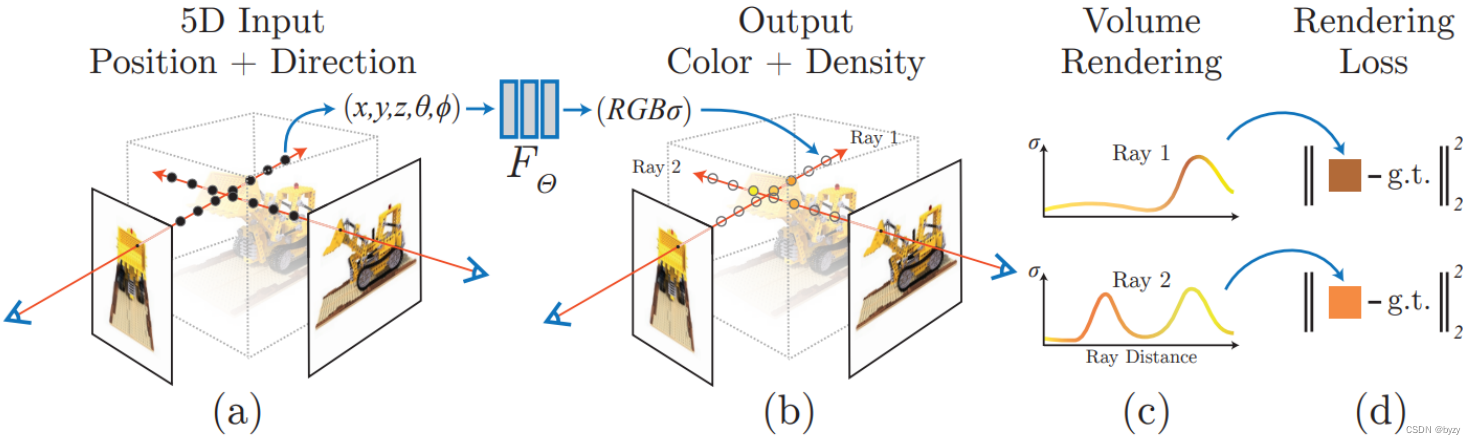
1. 对于待合成图像的每个像素，使用相机射线穿过场景并生成采样点（上图(a)）。
2. 对每个采样点，使用射线方向和采样位置，输入NeRF MLP计算局部颜色与密度（上图(a)与(b)之间的连接处）。
3. 使用体积网格渲染，从采样点的色彩和密度生成图像。

4. 体积网格渲染

  设相机射线为$r(t)=o+td$，其中$o$为相机位置，$d$为射线方向。则可按下式得到色彩$C(r)$：$$C(r)={\int }_{t_1}^{t_2}T(t)\cdot \sigma (r(t))\cdot c(r(t),d)\cdot dt$$其中$\sigma (r(t))$和$c(r(t),d)$为射线$r(t)$处的体积网格密度和颜色。
  $T(t)$为累积透明度，表示射线从$t_1$到$t$不被拦截的概率：$$T(t)=\exp \left(-{\int }_{t_1}^t\sigma (r(u))\cdot du\right)$$  通过追踪待合成图像的像素对应的相机射线，可计算积分。但是通常会通过分层抽样法来计算其近似值。具体来说，射线会被分为等长的$N$段，然后在各段内均匀抽样一个点，并用求和近似上面的积分：$$\hat{C}(r)=\sum _{i=1}^N{\alpha }_i{T}_i{c}_i,其中T_i=\exp \left(-\sum _{j=1}^{i-1}{\sigma }_j{\delta }_j\right)$$其中${\delta }_i$为采样点$i$与$i+1$的距离；$({\sigma }_i,c_i)$为射线上采样点$i$的密度和颜色（使用NeRF MLP计算）。${\alpha }_i$为采样点$i$处alpha合成的透明度/不透明度：$${\alpha }_i=1-\exp ({\sigma }_i{\delta }_i)$$

5. 期望深度计算

  期望的深度可使用积累透明度沿射线计算：$$d(r)={\int }_{t_1}^{t_2}T(t)\cdot \sigma (r(t))\cdot t\cdot dt$$上式同样可使用求和近似：$$\hat{D}(r)=\sum _{i=1}^N{\alpha }_i{t}_i{T}_i$$某些深度正则化方法会使用期望深度将密度限制为类似（在场景表面取峰值的）delta函数的形式，或是保证深度的平滑性。

6. 损失函数

  对每个像素，考虑其平方误差光度损失，以优化MLP参数。总损失为：$$L=\sum _{r\in R}\Vert \hat{C}(r)-C_{gt}(r){\Vert }_2^2$$其中$C_{gt}(r)$是与射线$r$关联像素的真实颜色，$R$是待合成图像的相机射线集合。

7. 位置编码

  NeRF模型通常会使用位置编码，因其有利于渲染图像的细节重建。原始的位置编码$\gamma$是在点$x$的坐标（归一化到$[-1,1]$）以及射线单位方向向量$d$的每个分量$v$上进行的：$$\gamma (v)=(\sin (2^0\pi v),\cos (2^0\pi v),\sin (2^1\pi v),\cos (2^1\pi v),\cdots ,\sin (2^{N-1}\pi v),\cos (2^{N-1}\pi v))$$其中$N$为用户定义的维度参数。