引言

以往我们遇到的深度学习问题中，对于神经网络的输入一般都是一个向量，输出可能是一个类别。如果增加输入的复杂度，例如输入的是多个向量，或者每次输入的向量的个数是会改变的。例如，在文字处理中，如果把一句话中的每一个单词作为一个向量，那么一个输入就会有多个向量，又因为不同样本的句子长度不同，所以每次输入的向量的个数也是会改变的。

那么输出会是什么情况呢？
第一种可能性是输入的每个向量都对应了一个输出，输入和输出的长度是一样的。例如输入一句话，让机器判断这句话中的每一个单词的词性，那么此时输入输出的长度就是一样的。
第二种情况是只需要输出一个label。例如文本情感分析，输入一句话让机器判断这句话是正面的还是消极的等等。
第三种情况是，不知道需要多少输出，由机器自己判断输出的数量。例如机器翻译，输入和输出是不同的语言。

本文主要介绍第一种情况的解决方案，这种情况又叫做 Sequence Labeling 。

Sequence Labeling

想要实现输入多个向量，输出同样数目的标签label，有一种解决方案就是FC（Fully-connected，一个神经网络），对于每一个向量执行一次FC，然后输出对应的标签。

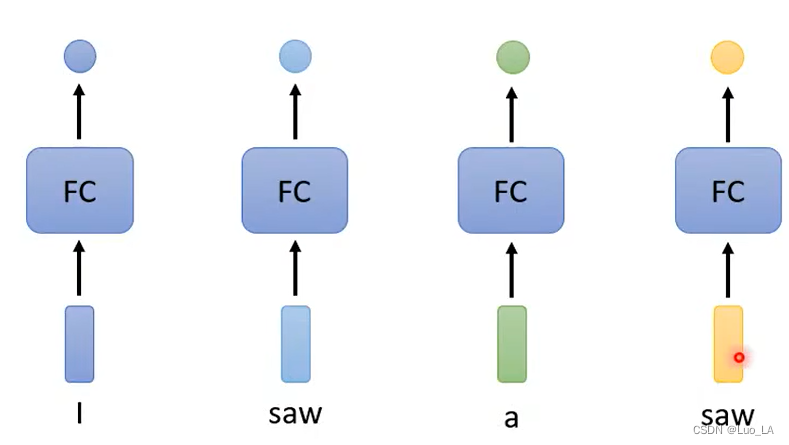
但是这样做有很大的弊端。例如在判断词性的例子中，我们将一句话作为一个输入，而一句话由多个单词组成，每个单词都有其对应的向量（向量的生成方式有两种，one-hot encoding 和 word embedding）。我们让每个单词都经过一次FC，得到其对应的词性。但是在上图的例子中，一句话中的两个saw是不同词性的，但是通过相同的网络得到输出没有理由是不一样的，因为输入的向量完全一样。

那么可以考虑这句话的上下文信息，把一个单词的相邻单词也考虑进去。一次输入一个window里面的向量。

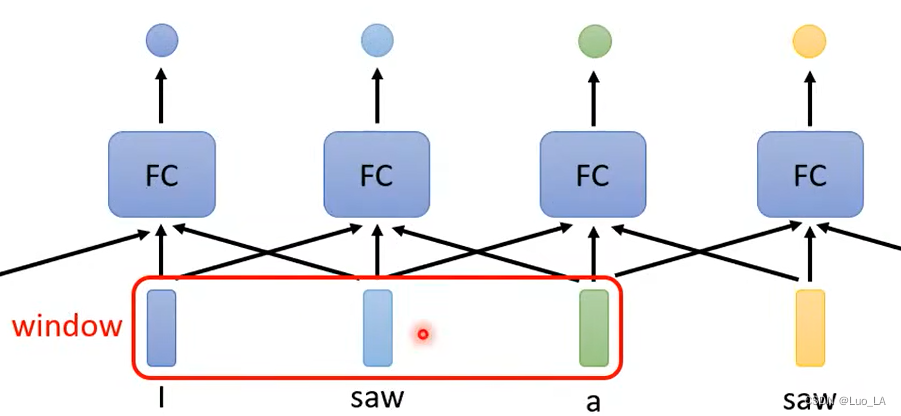
但是这样的方法还是有弊端，如果我们有一个任务不是要考虑一个window就可以解决的，而是要考虑整句话才能解决。那么把window设置成一句话的长度可以吗？显然不行，因为我们一开始就说过，每一个输入样本的长度是不定的。那么把window设置成所有样本输入中最长的那个样本的长度可以吗？看似可以，但是这样做会需要学习太多的参数，可能会造成过拟合。那么有什么解决方法呢？这就需要用到本文要介绍的 self-attention 机制。

Self-attention

Self-attention 是怎么应用的呢？ 首先要把一整个句子中的所有向量都经过 Self-attention，输入几个向量，就输出几个向量。得到的输出向量都考虑了整个句子的所有上下文信息。然后再将考虑了整句话信息的向量作为输入，进行FC得到对应的输出标签。

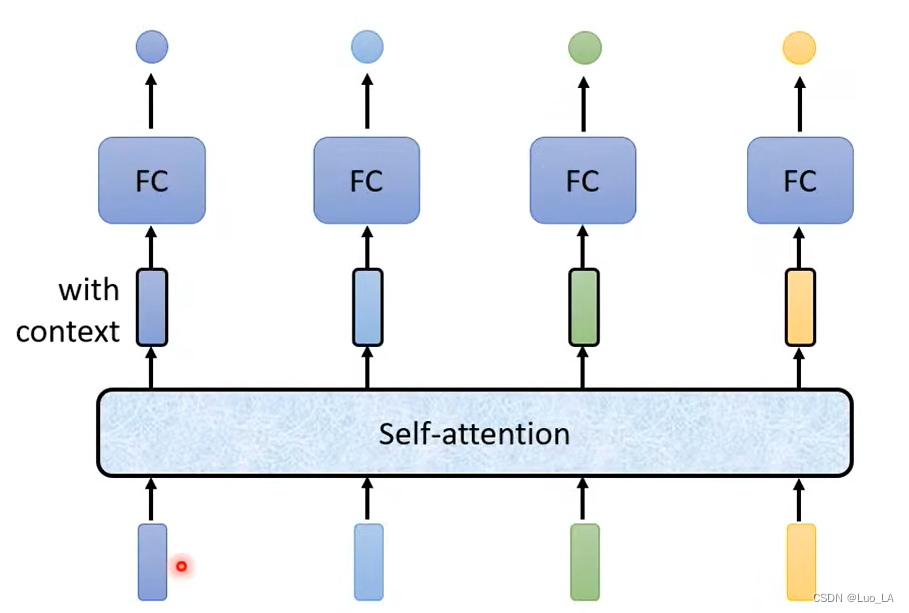
Self-attention 是怎么运作的呢？
首先 Self-attention 的输入是多个向量，这些向量可能是一整个神经网络的输入，也可能是某个隐藏层的输出，所以在这里用 $a$ 来表示输入。输出的向量用 $b$ 来表示，每一个 $b$ 都是考虑了所有的 $a$ 而生成的。下面我们介绍 $b$ 是如何产生的，以 $b^1$ 为例。

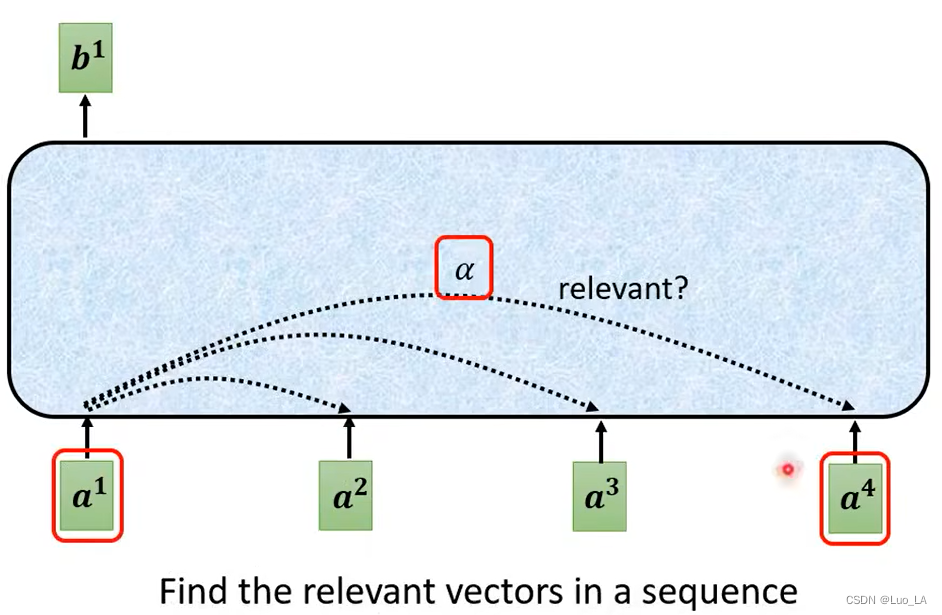
首先我们要根据 $a^1$ 找到整句话中和 $a^1$ 相关的其它向量。每一个相关的向量和 $a^1$ 的关联程度用一个数值 $\alpha$ 来表示。

那么我们怎么找到其它向量和 $a^1$ 之间的关联性呢？我们使用 Dot-product 的计算方式得到 $\alpha$ 。将两个向量作为输入，分别乘一个矩阵后得到两个新的矩阵 $q和k$，然后$q和k$做内积，得到一个数值就是 $\alpha$。

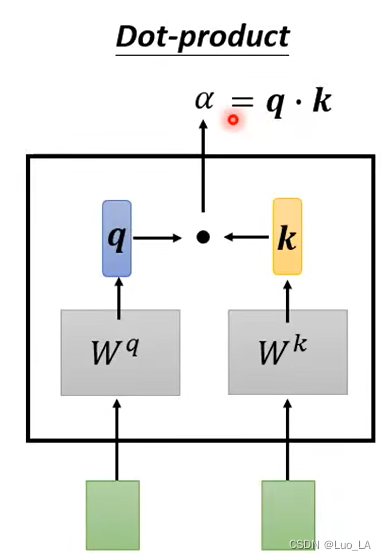
那么我们现在将这种得到 $\alpha$ 方式运用到我们的 self-attention 中。对于 $a^1$ ，我们要对它分别和 $a^2$ $a^3$ $a^4$ 计算关联性。首先 $a^1$ 乘上 $W^q$ 得到 $q^1$ 向量，$q^1$ 有个名字叫做 query。接下来 $a^2$ $a^3$ $a^4$ 都要乘上 $W^k$ 得到 $k$ 向量，$k$ 有个名字叫做 key。$q和k$ 做内积就得到了 $alpha$， $alpha$ 又叫做 attention score。${\alpha }_{1,2}$ 就表示 $a^1$ 和 $a^2$之间的 attention score。

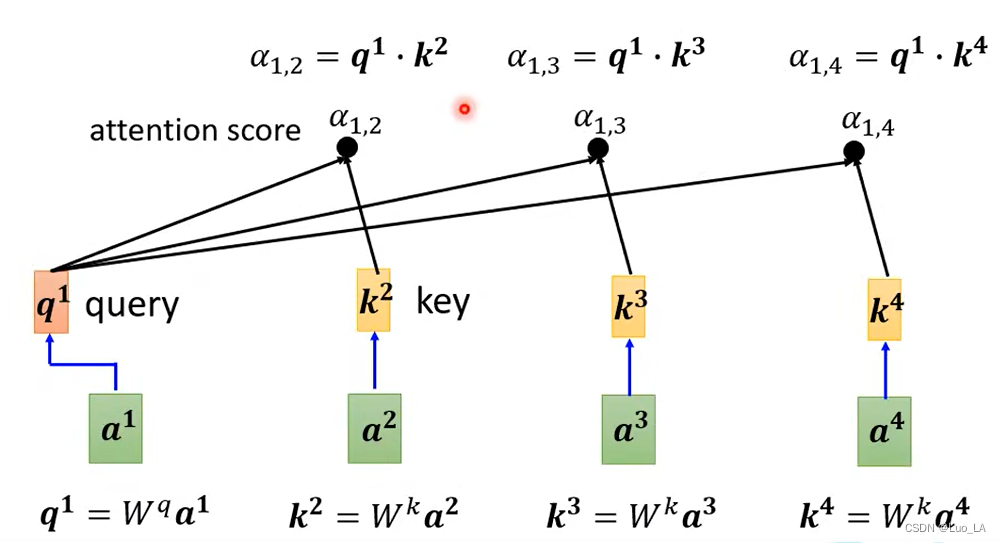
在实际操作中， $a^1$ 也要和自己计算关联性，也要将 $a^1$ 乘上 $W^k$ 得到 $k^1$ ，然后去计算自己的关联性。

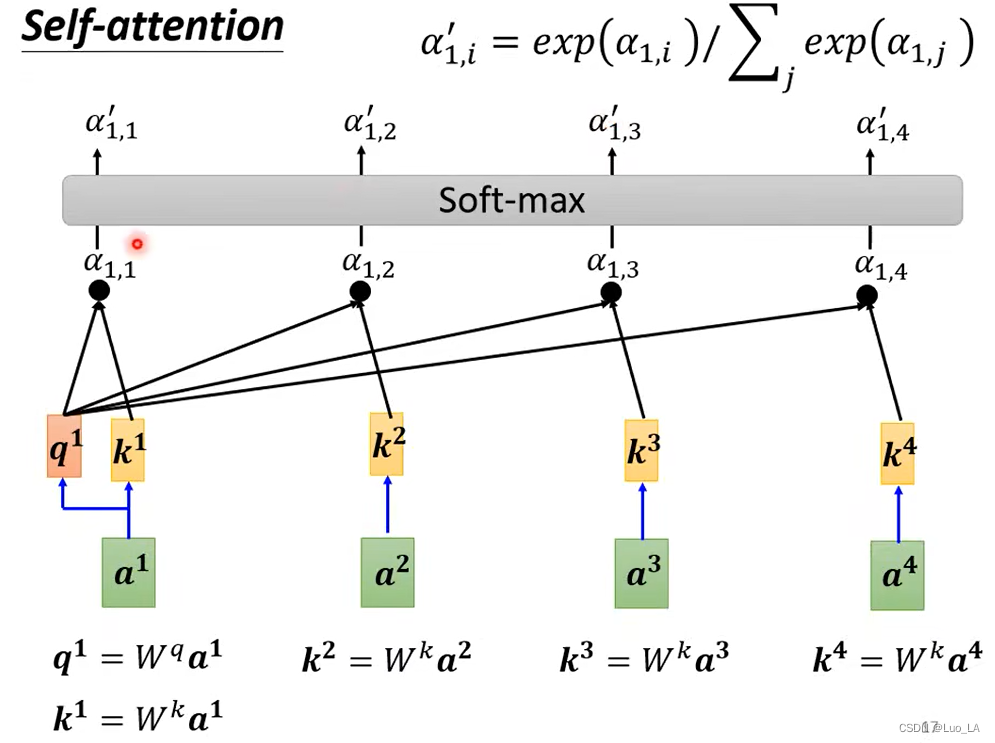
计算出 $a^1$ 和所有向量之间的关联性之后，接下来要做一个 soft-max，得到 ${\alpha }^{\prime }$。

然后我们根据 ${\alpha }^{\prime }$ 抽取出这句话中的重要信息。我们将输入的每个向量先乘一个矩阵 $W^v$ 得到新的向量 $v$，然后再对每个 $v$ 乘上对应的 ${\alpha }^{\prime }$ 再加起来就得到了向量 $b_1$。

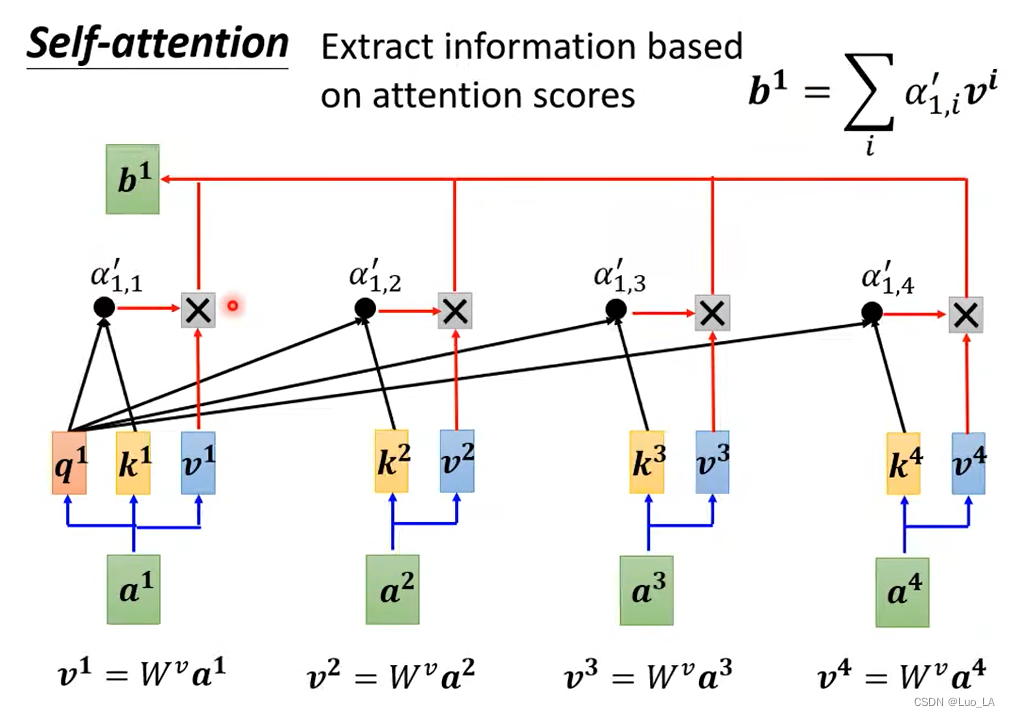
根据上面的介绍，我们会想象到，如果 $a^1$ 和 $a^2$ 的关联性比较强，${\alpha }_{1,2}^{{}^{\prime }}$ 得到的值比较大，那么最终得到的 $b^1$ 的值就可能会比较接近 $a^2$ 。

矩阵乘法

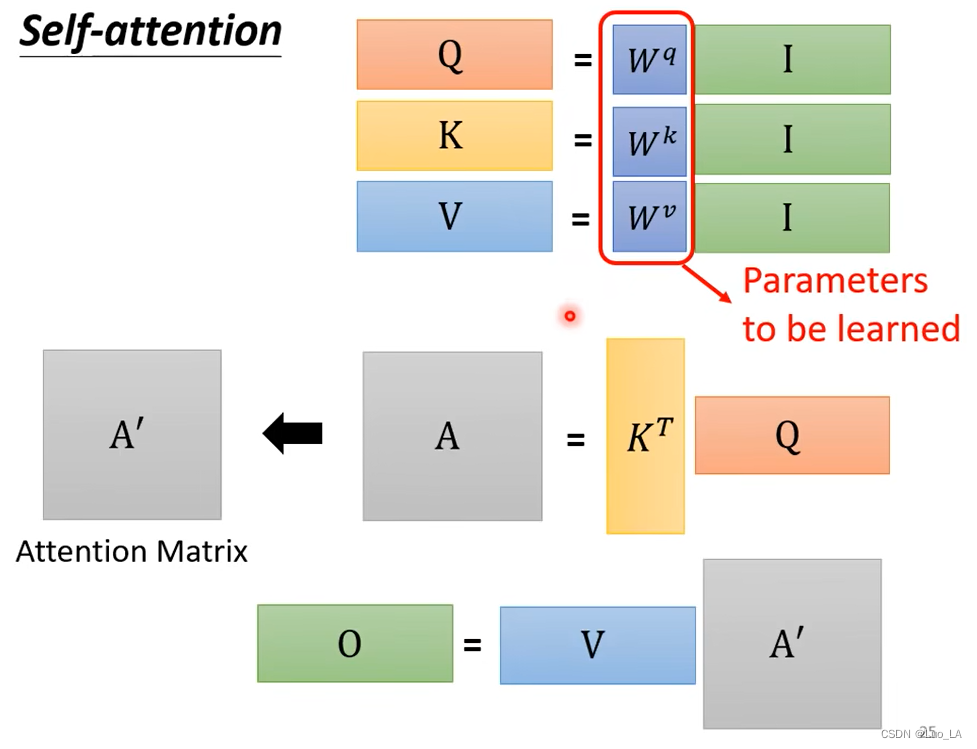
现在我们通过矩阵乘法的角度来看一看 self-attention 是怎样运作的。

第一步，以 $q$ 为例，因为每个 $a^i$ 都是乘一个矩阵得到对应的 $q^i$，$q^i=W^q{a}^i$。我们把 $a^i$ 拼接起来看作是一个矩阵 $I$，矩阵 $I$ 的每一列就是 self-attention 的每一个输入，然后对 $I$左乘矩阵 $W^q$，得到矩阵 $Q$， $Q$ 的每一列就是 $q^i$ 。同理，我们可以得到 $K,V$。

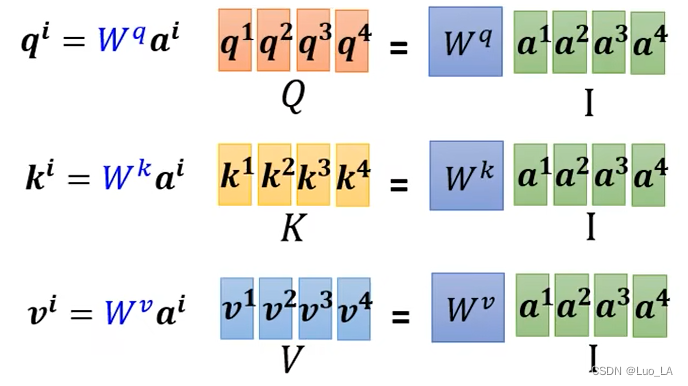
第二步，计算 attention score。我们把 $k^i$ 拼接起来看作一个矩阵 $K^T$，每个 $k^i$ 当作这个矩阵的一行，然后乘上矩阵 $q^1$，就得到了一个矩阵，这个矩阵的每一行就是 $a^1$ 的每一个与之关联的 attention score。

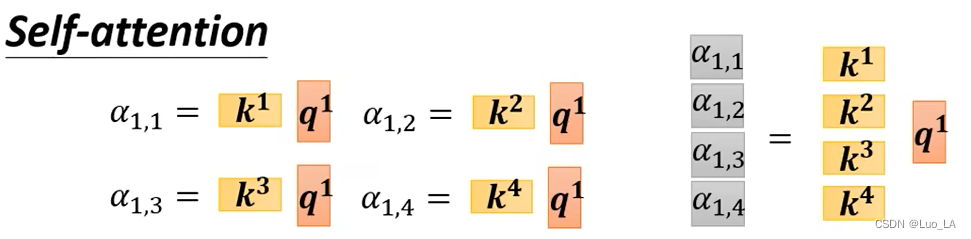
同理， $a^2,a^3,a^4$ 也要计算 attention score，我们把 $q^i$ 当作一个矩阵的列拼接成一个矩阵 $Q$。 $Q$ 左乘 $K^T$ 就得到了所有输入向量的 attention score，表示成矩阵 $A$，然后对 $A$ 的每一列做 soft-max。

第三步，我们计算输出。我们把 $v^i$ 拼接起来成矩阵 $V$，然后乘上矩阵 $A^{\prime }$，得到输出矩阵 $O$。

综上，self-attention 的运作机制其实就是一连串的矩阵乘法。在这一系列矩阵中，只有矩阵$W^q,W^k,W^v$是未知的，是需要通过训练学习的参数。

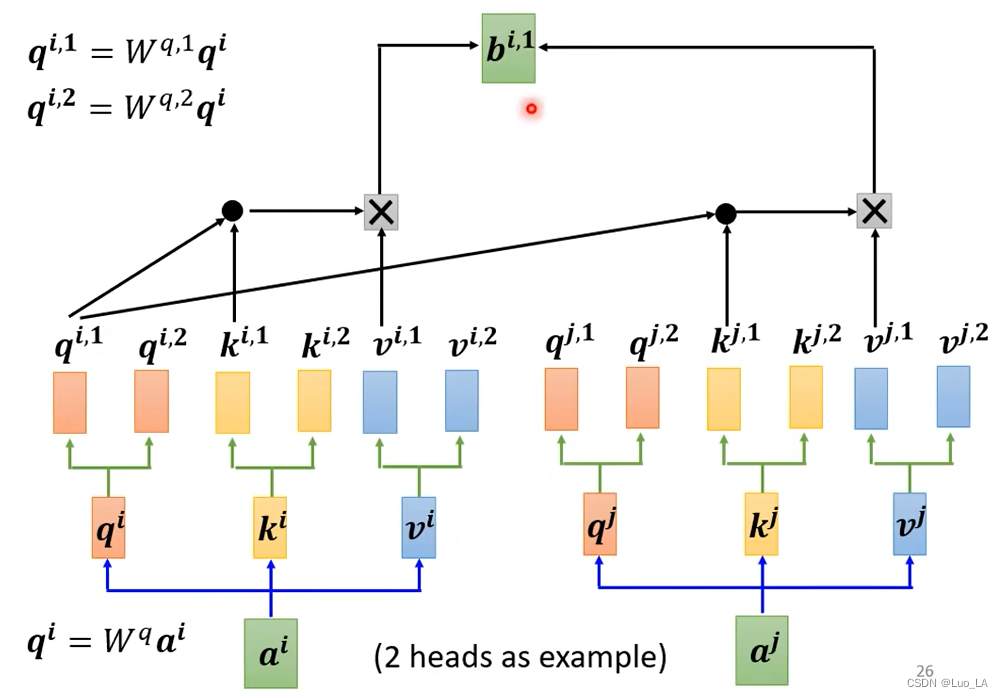
Muti-head Self-attention（多头注意力机制）

以 2 heads 为例，先把输入向量 $a$ 乘以一个矩阵得到 $q$，再把 $q$ 乘以两个不同的矩阵得到两个不同的 $q$，这两个 $q$ 用来表示两种不同的相关性。$q$ 有两个，对应的 $k和v$ 也都有两个。 然后分别计算得到 $b^{i,1}，b^{i,2}$。

把 $b^{i,1}，b^{i,2}$ 拼接起来，左乘一个矩阵，得到 $b^i$。