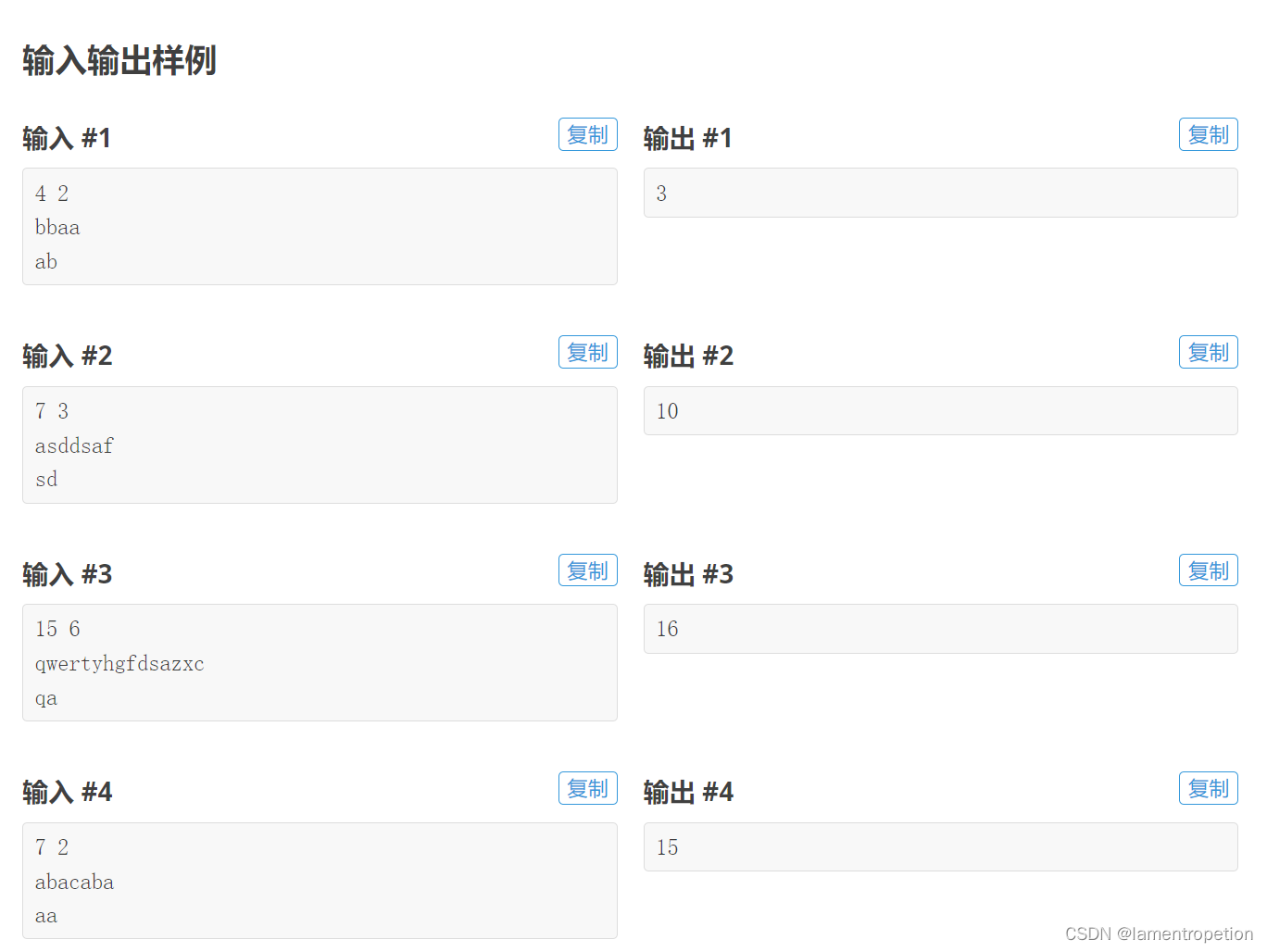
Problem - F - Codeforces

题意：

 

思路：

首先有个很明显的结论是：替换的字符一定是那两个字符之一

那么替换成哪个字符贡献更大不确定，因此考虑DP

因为有操作次数限制，直接把操作放进状态里

为了计算贡献，需要把前缀 t1 的数量也放进状态里

然后就暴力分类讨论转移就好了

#include <bits/stdc++.h>

using namespace std;

constexpr int N = 2e2 + 10;
constexpr int mod = 998244353;

std::string s, t;

int n, K;
int pre[N];
int dp[N][N][N];

void solve() {
    std::cin >> n >> K >> s >> t;
    s = " " + s;
    t = " " + t;

    //特判
    int cnt = 0;
    if (t[1] == t[2]) {
        if (K != 0) {
            for (int i = 1; i <= n; i ++) {
                if (s[i] != t[1]) {
                    s[i] = t[1];
                    cnt ++;
                    if (cnt >= K) break;
                }
            }
        }
        cnt = 0;
        for (int i = 1; i <= n; i ++) {
            if (s[i] == t[1]) cnt ++;
        }
        std::cout << cnt * (cnt - 1) / 2 << "\n";
        return;
    }
    for (int i = 1; i <= n; i ++) {
        pre[i] = pre[i - 1] + (s[i] == t[1]);
    }

    memset(dp, -0x3f, sizeof(dp));
    dp[0][0][0] = 0;
    for (int i = 1; i <= n; i ++) {
        for (int j = 0; j <= K; j ++) {
            for (int k = 0; k <= i; k ++) {
                //不操作
                if (s[i] != t[1] && s[i] != t[2]) {
                    dp[i][j][k] = std::max(dp[i][j][k], dp[i - 1][j][k]);
                } 
                if (s[i] == t[1] && k >= 1) {
                    dp[i][j][k] = std::max(dp[i][j][k], dp[i - 1][j][k - 1]);
                }
                if (s[i] == t[2]) {
                    dp[i][j][k] = std::max(dp[i][j][k], dp[i - 1][j][k] + k);
                }
                //操作
                //变为t1
                if (j >= 1 && k >= 1) dp[i][j][k] = std::max(dp[i][j][k], dp[i - 1][j - 1][k - 1]);
                //变为t2
                if (j >= 1) dp[i][j][k] = std::max(dp[i][j][k], dp[i - 1][j - 1][k] + k); 
            }
        }
    }

    int ans = 0;
    for (int j = 0; j <= K; j ++) {
        for (int k = 0; k <= n; k ++) {
            ans = std::max(ans, dp[n][j][k]);
        }
    }

    std::cout << ans << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t = 1;
    while(t --) {
        solve();
    }
    return 0;
}