来源:力扣(LeetCode)
描述:
给你一个 n 个节点的无向无根树,节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ,其中 coins[i] 可能为 0 也可能为 1 ,1 表示节点 i 处有一个金币。
一开始,你需要选择树中任意一个节点出发。你可以执行下述操作任意次:
- 收集距离当前节点距离为 2 以内的所有金币,或者
- 移动到树中一个相邻节点。
你需要收集树中所有的金币,并且回到出发节点,请你返回最少经过的边数。
如果你多次经过一条边,每一次经过都会给答案加一。
示例 1:
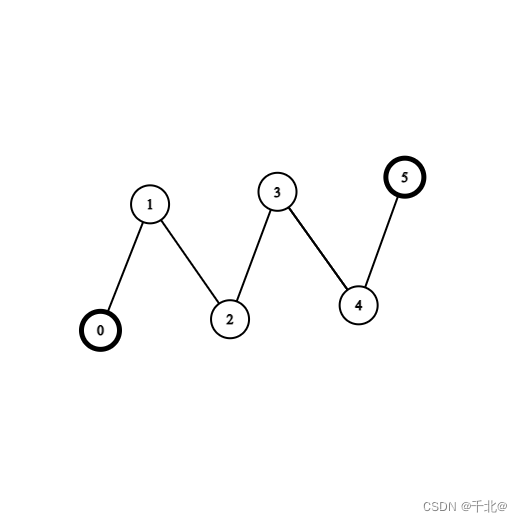
输入:coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
输出:2
解释:从节点 2 出发,收集节点 0 处的金币,移动到节点 3 ,收集节点 5 处的金币,然后移动回节点 2 。
示例 2:
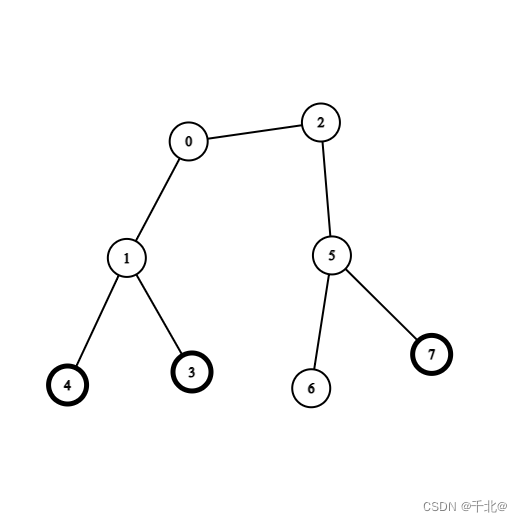
输入:coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
输出:2
解释:从节点 0 出发,收集节点 4 和 3 处的金币,移动到节点 2 处,收集节点 7 处的金币,移动回节点 0 。
提示:
- n == coins.length
- 1 <= n <= 3 * 104
- 0 <= coins[i] <= 1
- edges.length == n - 1
- edges[i].length == 2
- 0 <= ai, bi < n
- ai != bi
- edges 表示一棵合法的树。
方法:两次拓扑排序
思路与算法
对于给定无根树中度数为 111 的节点,我们称其为「叶节点」。可以发现,对于每一个「叶节点」l,如果 l 上没有金币,那么我们就没有必要走到 l。这是因为对于 l 唯一相邻的那个节点 l′ ,它可以收集到在 l 可以收集到的所有金币,那么:
-
如果我们从 l 开始出发,那么可以改成从 l′ 开始出发,经过的边数一定减少;
-
如果我们不从 l 开始出发,那么到达 l′ 之后不必再走向 l,经过的边数一定减少。
因此,我们可以不断地移除给定无根树中没有金币的「叶节点」。当某个「叶节点」被移除后,它唯一相邻的那条边也需要被移除,这样可能会有新的节点变为「叶节点」。我们不断迭代地重复这个过程,直到所有的「叶节点」上都有金币为止。
这一步可以使用基于广度优先搜索的拓扑排序解决。我们首先将所有「叶节点」加入队列中,随后不断从队列中取出节点,将它标记为删除,并判断其唯一相邻的节点是否变为「叶节点」。如果是,就将相邻的节点也加入队列中。
当所有的「叶节点」上都有金币时,我们应该如何解决给定的问题呢?我们可以先思考,如果操作变为「收集距离当前节点距离为 0 以内的所有金币」该如何解决。当距离为 0 时,我们必须要走到对应的节点上才能收集金币,而每个「叶节点」上都有金币,因此我们必须遍历到所有的「叶节点」,这也意味着我们遍历了整颗树。从任一节点出发,遍历整颗树并返回原节点,会经过树上的每条边一次,而树的边数等于点数减一,因此答案为 2(n′ − 1) ,其中 n′ 时经过上文移除后,无根树中节点的数量。
如果操作变为「收集距离当前节点距离为 1 以内的所有金币」呢?我们可以进一步思考得到:当我们即将遍历到「叶节点」时,可以直接返回,因为此时我们与「叶节点」的距离为 1,可以直接收集到金币,不需要走到「叶节点」。因此,我们遍历的范围,就是将树中所有叶节点以及它们唯一相邻的那条边移除后的新树。在新树中的金币可以通过遍历获得到,而不在新树中的金币会在遍历到与其距离为 1 的某个节点时获取到。
因此,当操作变为「收集距离当前节点距离为 2 以内的所有金币」时,我们的方法仍然是类似的,我们只需要将新树中所有的「叶节点」以及它们唯一相邻的那条边移除,得到的新新树就是需要遍历的范围。
这一步同样可以使用基于广度优先搜索的拓扑排序解决。我们进行 222 次如下的操作:首先将所有「叶节点」加入初始队列中,随后不断从初始队列中取出节点,将它标记为删除。
细节
如果 新新树 中没有任何节点,说明在初始的无根树中,存在一个节点可以直接获取到所有金币,答案为 0,否则答案为 2× ( 新新树 中的节点数量 −1)。
代码:
class Solution {
public:
int collectTheCoins(vector<int>& coins, vector<vector<int>>& edges) {
int n = coins.size();
vector<vector<int>> g(n);
vector<int> degree(n);
for (const auto& edge: edges) {
int x = edge[0], y = edge[1];
g[x].push_back(y);
g[y].push_back(x);
++degree[x];
++degree[y];
}
int rest = n;
{
/* 删除树中所有无金币的叶子节点,直到树中所有的叶子节点都是含有金币的 */
queue<int> q;
for (int i = 0; i < n; ++i) {
if (degree[i] == 1 && !coins[i]) {
q.push(i);
}
}
while (!q.empty()) {
int u = q.front();
--degree[u];
q.pop();
--rest;
for (int v: g[u]) {
--degree[v];
if (degree[v] == 1 && !coins[v]) {
q.push(v);
}
}
}
}
{
/* 删除树中所有的叶子节点, 连续删除2次 */
for (int _ = 0; _ < 2; ++_) {
queue<int> q;
for (int i = 0; i < n; ++i) {
if (degree[i] == 1) {
q.push(i);
}
}
while (!q.empty()) {
int u = q.front();
--degree[u];
q.pop();
--rest;
for (int v: g[u]) {
--degree[v];
}
}
}
}
return rest == 0 ? 0 : (rest - 1) * 2;
}
};
时间 764ms 击败 32.86%使用 C++ 的用户
内存 216.27MB击败 50.00%使用 C++ 的用户
复杂度分析
- 时间复杂度: O(n)。构造图的邻接表,度数数组以及拓扑排序都需要 )O(n) 的时间。
- 空间复杂度: O(n)。即为图的邻接表,度数数组以及拓扑排序中的队列需要使用的空间。
author:力扣官方题解