栈

用两个栈实现队列

栈：只允许在一头进行入队和出队，先进后出

队列：只允许一头入队，另一头出队，先进先出

如果先都放入一个栈中，就是倒序的，然后再把第一个栈中的元素依次移动到另一个栈中，又倒了一次序，就是正序了，即先进先出

class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }//先都放入一个栈中

    int pop() {
        int res;
        while(!stack1.empty()){
            stack2.push(stack1.top());//把第一个栈中的元素倒到第二个栈中
            stack1.pop();
        }
        res=stack2.top();//此时第二个栈的第一个元素就是最先入队的元素
        stack2.pop();
        while(!stack2.empty()){
            stack1.push(stack2.top());//再把第二个栈的元素都倒到第一个中，目的是为了下一步的入队，即从尾部放入元素
            stack2.pop();
        }
        return res;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

包含min函数的栈

有一个误区是，只用一个值存储当前栈的最小值，但如果这个最小值出栈后，就没了

所以函数就是要，根据栈的状态，时刻更新最小值

那就是说当前栈有几个元素，就应该用几个元素保存最小值，表示分别在栈有几个元素时所存储的最小值

所以用两个栈，一个栈就是存值的，另一个就是当前栈的最小值，那么操作就是每入栈一个元素，就和上个Min栈中的栈顶元素（表示前面所有元素的Min)比较,如果比它小，就让当前的栈的min为这个新入的元素，如果不是，那就依旧保留之前的min,直到遇到一个比它小的才更新。

stack<int>common;
stack<int>minnum;
void push(int val) {
	common.push(val);
	if (minnum.empty() || minnum.top() > val) {
		minnum.push(val);
	}
	else {
		minnum.push(minnum.top());
	}
}
void pop() {
	common.pop();
	minnum.pop();
}
int top() {
	return common.top();
}
int min() {
	return minnum.top();
}

有效括号序列 

遇到左括号序列就入栈，遇到右括号序列就出栈

最后如果栈有余或者遇到右括号但是栈为空，就是false

怎么保证遇到的右括号是和当前左括号栈的栈顶元素匹配？

不应该让左括号系列入栈，而是应该让接下来期望遇到的元素入栈，如果还是左括号序列，就接着入栈期望元素，如果遇到了不是左括号序列的元素，那么正确的必须是栈顶元素的期望的元素，不然就是错误的。

stack<int>s1;
for (int i = 0; i < s.length(); i++) {
	if (s[i] == '(') {
		s1.push(')');
	}
	else if (s[i] == '[') {
		s1.push(']');
	}
	else if (s[i] == '{') {
		s1.push('}');
	}
	if (s1.empty()) {
		return false;
	}
	else if (s1.top() == s[i]) {
		s1.pop();
	}
}
return s1.empty();

火车入栈问题

题意为根据入栈顺序判断能否给出指定的出栈顺序

用三个栈，一个栈为入栈顺序，一个栈为出栈顺序，一个辅助栈来模拟

根据入栈顺序，依次入栈，每入栈一个元素，就判断一下和当前出栈顺序的栈顶元素是否相同，如果不相同，接着按照入栈顺序往辅助栈里入元素，直到当前元素和出栈顺序的栈顶元素相同，就开始尝试出栈，直到当前元素和出栈顺序的栈顶元素不同，再接着入栈

可以有剪枝，就是如果原入栈是单调的，那么

最后如果入栈栈空了，辅助栈的栈顶元素和出栈栈的栈顶元素不同，那就是false

关于指定栈元素数量的出栈可能情况有多少种

思路1：根据第一个元素的出栈顺序，完成一次情况的划分

分析：1) 如果元素a在1号位置，那么只可能a进栈，马上出栈，此时还剩元素b、c、d等待操作，就是子问题f (3)； 2) 如果元素a在2号位置，那么一定有一个元素比a先出栈，即有f (1)种可能顺序（只能是b），还剩c、d，即f (2)， 根据乘法原理，一共的顺序个数为f (1) * f (2)； 3) 如果元素a在3号位置，那么一定有两个元素比1先出栈，即有f (2)种可能顺序（只能是b、c），还剩d，即f (1)， 根据乘法原理，一共的顺序个数为f (2) * f (1)； 4) 如果元素a在4号位置，那么一定是a先进栈，最后出栈，那么元素b、c、d的出栈顺序即是此小问题的解，即 f (3)； 结合所有情况，即f (4) = f (3) + f (2) * f (1) + f (1) * f (2) + f (3); 为了规整化，我们定义f (0) = 1；于是f (4)可以重新写为： f (4) = f (0)*f (3) + f (1)*f (2) + f (2) * f (1) + f (3)*f (0) 然后我们推广到n，推广思路和n=4时完全一样，于是我们可以得到： f (n) = f (0)*f (n-1) + f (1)*f (n-2) +... + f (n-1)*f (0)

第一个元素在几号位置，就说明在入栈栈紧邻的后面几个元素入了栈，由它确定一个栈区间（这个区间里除了第一个元素之外怎么出的不管，但是要保证第一个元素是这个区间最后一个出的），然后出栈消除掉。之后就是下一个剩余规模的的第一个元素出栈位置问题。

思路2：根据最后出栈的元素，完成一次情况的划分

1……k……n，第k个元素最后出栈的可能情况

k最后出栈，表明k入栈时，栈里没有元素，即k-1前的元素都已完成，和k之后的没关系，独立过程。同时表明，k出栈时，k后的元素都已完成出栈，即以k为端点确定了两个栈区间。

k之前怎么出的我不管，k之后怎么出的也不管，但是要保证没有出k，即k入栈后就一直没动过，直到都动完了最后再出k

前者是说k-1的规模，后者是说n-k（不包含k，即k+1到n,共有n-k-1+1个数)的规模,(相加即n-1,少的1就是k）

 

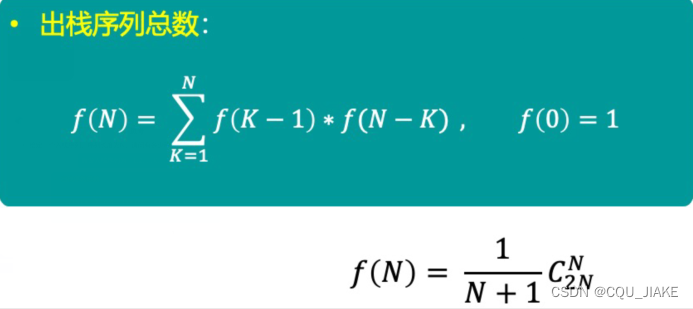
Catalan数