一、基本知识
1、基本统计量
- 总体:研究对象的某个感兴趣的指标。
- 样本:从总体中随机抽取的独立个体X1,X2,…,Xn,一般称(X1,…,Xn)为一个样本,可以看成一个n维随机向量,它的每一取组值(x1,…,xn)称为样本的观测值。
- 统计量:样本是总体的代表,抽取后不直接利用样本的观测值进行推断,而是把样本所包含的有关信息集中起来进行研究,即针对研究的目的构造样本的某种函数,称为样本函数,只包含样本信息的样本函数就是统计量。根据研究目的,下面介绍常见的统计量。
平均值、中位数、众数、方差、均方差(标准差)、极差就不介绍了。
- 分位数:满足
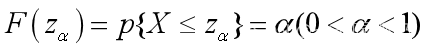 的Zα称为分布函数F的α分位数。
的Zα称为分布函数F的α分位数。 - 偏度:
 反映数据分布对称性指标。 当P1>0是称为右偏,即数据位于均值右边的居多;当P1<0是左偏,即数据位于均值左边的居多;当P1≈0时,数据分布关于均值对称。
反映数据分布对称性指标。 当P1>0是称为右偏,即数据位于均值右边的居多;当P1<0是左偏,即数据位于均值左边的居多;当P1≈0时,数据分布关于均值对称。 - 峰度:
 。计算正态分布的峰度值为3(均匀分布的峰度是1.8),若P2>3,表示数据分布有沉重的尾巴,即很多数据离均值较远。
。计算正态分布的峰度值为3(均匀分布的峰度是1.8),若P2>3,表示数据分布有沉重的尾巴,即很多数据离均值较远。 - k阶原点矩:

- k阶中心矩:
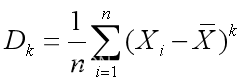
- 变异系数(Coefficient of Variation):
 (两组变量量纲不同时的差异程度比较),常常用于反映重要程度的权系数。
(两组变量量纲不同时的差异程度比较),常常用于反映重要程度的权系数。
二、统计回归模型基础
1、回归模型
处于同一个大系统下各个变量,它们相依存,相互制约,却又不能判定为确定的函数关系,这类关系称为相关关系。例如作物的产量与施肥量相关,人的身高与体重相关。
一般地,考虑多个变量的情形,将考察的目标的变量Y称为因变量,而影响它的其它各个变量称为自变量或可控变量。在给定可控变量X1,X2,…,Xp的一组观测值x1,x2,…,xp,若Y的条件数学期望 存在,称其为Y关于X1,X2,…,Xp的回归函数。
存在,称其为Y关于X1,X2,…,Xp的回归函数。
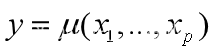 称为Y对X1,…,Xp的回归方程。
称为Y对X1,…,Xp的回归方程。
 【2.1】称为Y对X1,…,Xp的回归模型。特别当
【2.1】称为Y对X1,…,Xp的回归模型。特别当![]() 时,称【2.1】为正态回归模型,其中ε表示模型的拟合误差,又称为残差或随机扰动项。理想的模型应当是
时,称【2.1】为正态回归模型,其中ε表示模型的拟合误差,又称为残差或随机扰动项。理想的模型应当是![]()
![]() 越小越好。
越小越好。
回归函数μ(x1,…,xp)是确定性的函数,一般不知道,只能通过经验公式S(x1,…,xp)来作为其估计函数,记为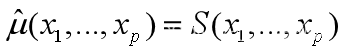 习惯上称
习惯上称 为经验回归方程。
为经验回归方程。
回归与拟合的区别:
回归和拟合是统计学中常用的两个概念,它们有一些相似之处,但也有一些不同之处。
回归是指通过分析数据的关系,建立一个模型来描述自变量和因变量之间的关系。回归分析的目标是预测因变量的值,并评估自变量对因变量的影响程度。回归可以用于解决预测和关联分析等问题。
拟合是指将一个数学模型与已有的数据拟合,以找到最能代表这些数据的模型参数。拟合的目标是通过调整模型的参数值,使得模型的预测值与实际观测值之间的误差最小化。拟合可以用于寻找最佳拟合曲线或曲面等。
总的来说,回归和拟合都是通过建立数学模型来描述数据的变化趋势和关系。回归更关注变量之间的关系和预测能力,而拟合更关注模型与数据之间的拟合程度。
2、线性回归模型和多项式回归模型
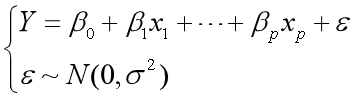 【2.2】
【2.2】
为p元线性回归模型,其中 是回归系数。
是回归系数。
 【2.3】
【2.3】
为p阶多项式回归。
由于【2.2】有较好的检验和误差分析,常常把【2.3】转化为【2.2】: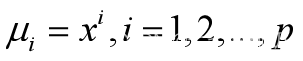 就将p阶多项式回归转换为p元线性回归。
就将p阶多项式回归转换为p元线性回归。
3、回归系数求解
回归模型的系数采用最小二乘估计法,对Y,X1,…,Xp作了n次观测,得到系列观测值
构造函数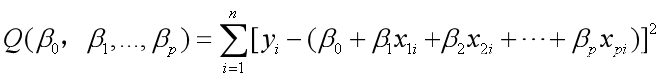
为了求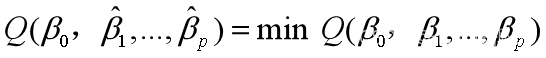 (即求关于β0,β1,…,βp的最小值)
(即求关于β0,β1,…,βp的最小值)
记

称SST为总偏差平方和(即y1,y2,…,yn之间的误差)
称SSE为残差平方和(即预测值与真实值之间的误差)
称SSR为回归平方和(即回归自变量引起的误差)
 为观测值对应的理论值。
为观测值对应的理论值。
在假设H0: 不全为0,
不全为0,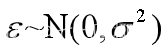 成立的情况下,可以推出
成立的情况下,可以推出 且相互独立。
且相互独立。
建模的目的,主要是用自变量x的变化来解释因变量y的变化,即希望SST值主要是SSR引起的,SSE很小,而由概率统计知识知道
 【2.4】
【2.4】
给定显著水平α,查F分布临界值![]() 若由【2.4】算出来的F值满足F>Fα(p,n-p-1)就认为SSR远远大于SSE,即模型有效。
若由【2.4】算出来的F值满足F>Fα(p,n-p-1)就认为SSR远远大于SSE,即模型有效。
同时,由于

即在模型有效时,可以用SSE/(n-p-1)来作为σ2的无偏估计值。
显著水平:
在统计学中,显著水平(significance level)指的是在假设检验中作为判断标准的阈值。它用来评估统计检验结果是否足够显著,即对于给定的观察数据,是否可以拒绝原假设。
一般来说,显著水平通常以 α(alpha)表示,取值范围在0到1之间。常见的显著水平有0.05(或5%)和0.01(或1%)等。α的选择通常取决于具体情况和研究的要求。
在进行假设检验时,我们首先设定一个原假设(null hypothesis),通常表示没有效应或没有关系,然后根据观察数据计算统计量,并计算出相应的p值(p-value)。p值表示观察数据达到或超过统计量所示的极端情况的概率。
然后,我们将p值与预先设定的显著水平进行比较。如果p值小于或等于显著水平,通常就拒绝原假设,认为观察数据具有统计显著性。反之,如果p值大于显著水平,就无法拒绝原假设,没有足够的证据表明观察结果是显著的。
显著水平的选择需要权衡研究的目的、统计方法和实际需求。通常,较低的显著水平要求有更强的证据才能拒绝原假设,但也可能增加犯第一类错误(拒绝真实的原假设)。而较高的显著水平则减少了犯第一类错误的可能性,但也增加了犯第二类错误(接受错误的原假设)的风险。
4、回归显著性检验
(1)回归方程显著性检验问题:软件计算R2和F值
在回归方程的显著性检验中,R方(R-Squared)和F值(F-value)是常用的统计指标。
R方是衡量回归方程对观察数据的拟合程度的一个度量。它的取值范围在0到1之间,越接近1表示回归方程能够很好地解释观察数据的变异。R方可以解释因变量的变异中,由回归方程中的自变量解释的比例。然而,它并不能直接说明回归方程是否显著。
F值是用于检验回归方程的整体显著性的统计量。它基于回归方程中解释的变异与未解释的变异之间的比例。F值的计算涉及一系列步骤,其中包括计算均方差、残差平方和、回归平方和等。F值的计算结果会与自由度相关,并进行与显著水平的比较。
在实际应用中,许多统计软件(如R、Python中的statsmodels和scikit-learn、SPSS、Excel等)都可以计算回归方程的R方和F值。这些软件会自动给出关于回归方程显著性的统计结果和相应的p值。一般来说,如果F值的p值小于预先设定的显著水平(如0.05),则可以认为回归方程是显著的,即至少有一个自变量对因变量的解释能力是统计显著的。
需要注意的是,R方和F值虽然是回归分析的重要指标,但不应作为唯一的判断依据。在实际应用中,还应综合考虑其他指标、模型的实际意义以及研究的背景和目的。
(2)回归系数显著性检验问题:T检验
T检验是用于检验回归模型中回归系数的显著性的一种统计方法。它通过计算回归系数的估计值与其标准误之比得到T值,并与自由度相关的T分布进行比较来判断回归系数的显著性。
在回归模型中,每个自变量都有一个相应的回归系数,用于衡量该自变量对因变量的影响程度。T检验用于检验每个回归系数是否显著不等于零,即判断自变量是否对因变量的解释能力是统计显著的。
T检验中使用的统计量是T值,它的计算公式为回归系数的估计值与其标准误之比。T值的计算结果与自由度相关,并与T分布进行比较。一般而言,如果T值的绝对值较大,那么说明回归系数显著不等于零,即自变量对因变量的解释能力是统计显著的。
在实际应用中,许多统计软件(如R、Python中的statsmodels和scikit-learn、SPSS、Excel等)都可以计算回归系数的T值和相应的p值。p值是在零假设成立的情况下观察到的T值或更极端结果的概率。一般而言,如果回归系数的p值小于预先设定的显著水平(如0.05),则可以认为该回归系数是显著的。
需要注意的是,T检验只能检验单个系数的显著性,而不能判断多个系数之间的比较。此外,在进行T检验时,还应满足检验的前提条件,如误差项的正态性、方差齐性等。此外,通过T检验得出的显著性是基于样本数据的推断,仍需要根据具体研究的背景和目的判断其实际意义和重要性。
(3)回归方程“最优”问题:经验调整
在回归分析中,经验调整(empirical adjustment)是一种通过对回归方程进行调整以获得更好拟合和更准确的预测的方法。
回归方程的拟合程度可以由R方值(R-squared)来衡量,R方值越接近1表示模型对数据的解释能力越强。然而,仅仅使用R方值来选择最佳模型可能存在问题,因为一个复杂的模型可以通过增加自由度而提高拟合程度,但可能过度拟合了数据,导致在新数据上表现不佳。
经验调整的目标是在保持模型解释力的同时,尽量避免过度拟合。一种常见的经验调整方法是利用特定的准则来选择自变量的子集,例如AIC(赤池信息准则)或BIC(贝叶斯信息准则)等。这些准则考虑了模型的拟合程度和模型的复杂度,鼓励选择较简单的模型,以避免过度拟合。
另一个常用的经验调整方法是交叉验证(cross-validation)。交叉验证将数据集分为训练集和验证集,使用训练集来拟合模型,并使用验证集评估模型的预测性能。通过比较不同模型的平均误差或其他性能指标,可以选择具有较好预测性能的模型。
需要注意的是,经验调整不是一种唯一的方法,适用于所有情况。选择最佳的经验调整方法将取决于具体的数据特征、研究目标和背景知识。在进行经验调整时,应该根据问题的要求和假设仔细选择模型和调整方法,同时要避免过度调整或过度拟合的问题。
要注意的是,给定显著水平α,计算F值与临界值![]() 比较即可;计算R值,与临界值
比较即可;计算R值,与临界值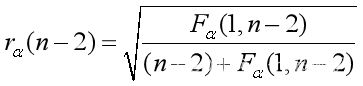 关于t检验也可以由系数的1-a置信区间估计来完成:若置信区间内包含0,则相应的系数显著为0,否则就不显著。(很多统计参考书,称R为可决系数,即可解释机会)
关于t检验也可以由系数的1-a置信区间估计来完成:若置信区间内包含0,则相应的系数显著为0,否则就不显著。(很多统计参考书,称R为可决系数,即可解释机会)