=========================================================================
个人主页
代码仓库
C语言专栏
初阶数据结构专栏
Linux专栏
=========================================================================
接上篇二叉树和堆的引入
=========================================================================
目录
前言
建堆
插入数据向上调整算法建堆
移动数据向上调整算法建堆
无序数组从H-1层向上移动的向下调整算法建堆
堆排序
TOP-K问题
前言
上篇文章详细讲解了堆,最后在执行完整代码后我们发现在删除堆中的数据时可以实现排序,当然这不是偶然,一切都是有迹可循的,今天就来讲解下用堆来实现排序,以及使用堆排序解决TopK问题。
建堆
插入数据向上调整算法建堆
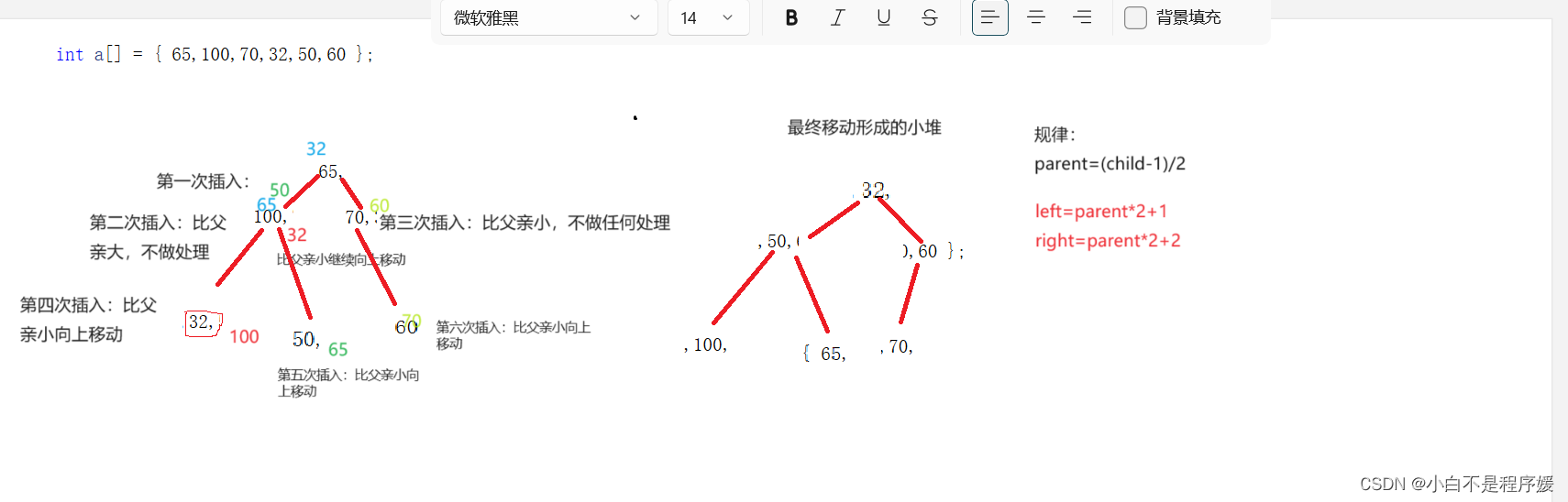
上篇文章中我们就实现了这个步骤,在主函数中创建了个数组然后将数组中的每个数据使用插入函数和向上调整算法函数依次插入动态开辟的空间中,每插入一个数据作为孩子和父亲相比较,根据大小交换位置,最终实现大/小堆。
插入函数
void HPPush(HP* php, HPDatatype x)
{
assert(php);
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDatatype* tmp = (HPDatatype*)realloc(php->a, sizeof(HPDatatype)*newcapacity);
if (tmp == NULL)
{
perror("realloc failed");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size] = x;
php->size++;
HPadjustUp(php->a, php->size-1);
}进入函数首先判断空间大小是否足够 ,不够的话使用realloc库函数开辟空间,开辟不成功直接退出,开辟成功的话赋值和修改size和容量。
向上调整函数和交换函数
void HPadjustUp(HPDatatype* a, int child)
{
//找到父亲
int parent = (child - 1) / 2;
//根为0 当和根交换后child为0
while (child > 0)
{
//当child小时和父亲交换 建成小堆
//当child大时和父亲交换 建成大堆
if (a[parent] > a[child])
{
swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}进入向上调整函数根据我们上篇内容提供父亲和孩子之间下标的关系,依次向上调整根据我们的需要和父亲孩子的大小关系,用交换函数实现大/小堆。
void swap(HPDatatype* x, HPDatatype* y)
{
HPDatatype tmp = *x;
*x = *y;
*y = tmp;
}
为防止局部变量出交换函数作用域被销毁,这里我们使用指针交换。
这种方式的缺点:
1.需要动态开辟空间,造成空间浪费。
2.需要完整的堆实现的代码,比较麻烦不是很推荐。
我们可以使用下面的方法对上面的函数进行优化。
移动数据向上调整算法建堆
根据我们这个方法的名字就可以判断我们这个方法是不需要动态开辟额外的空间,只需要使用数组下标通过向上调整算法函数来实现。
实现代码
for (int i = 1; i < n; i++)
{
HPadjustUp(a, i);
}这里我们将数组中的第一个数据作为一个堆通过下标的移动让后面的数字和前面的数字比较,也就相相当于前面的数字作为父亲后面的数字作为孩子,父亲和孩子使用向上调整函数进行调整实现堆。
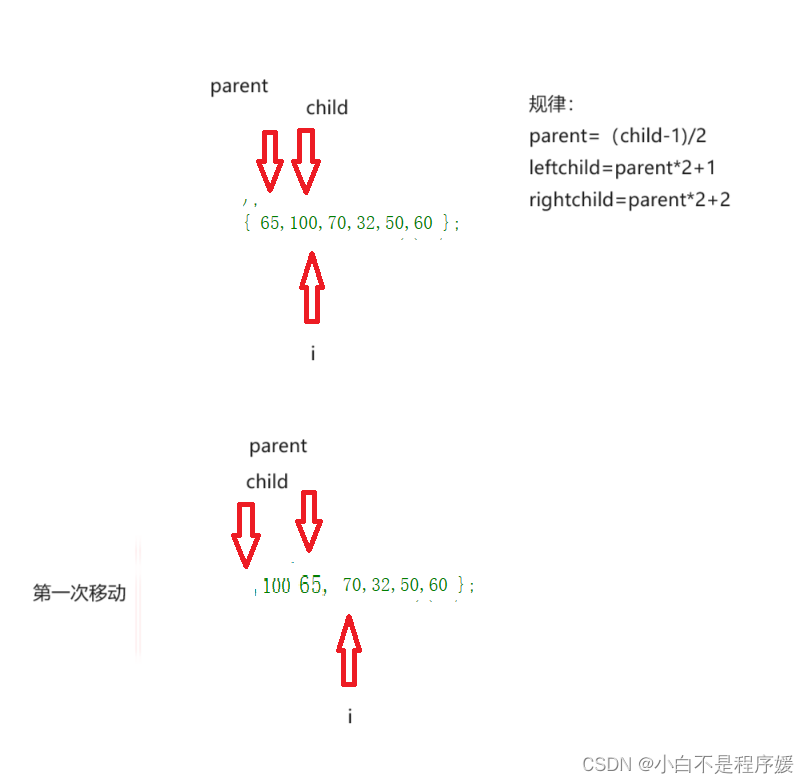
像这样经过多次的移动就形成我们的堆。
无序数组从H-1层向上移动的向下调整算法建堆
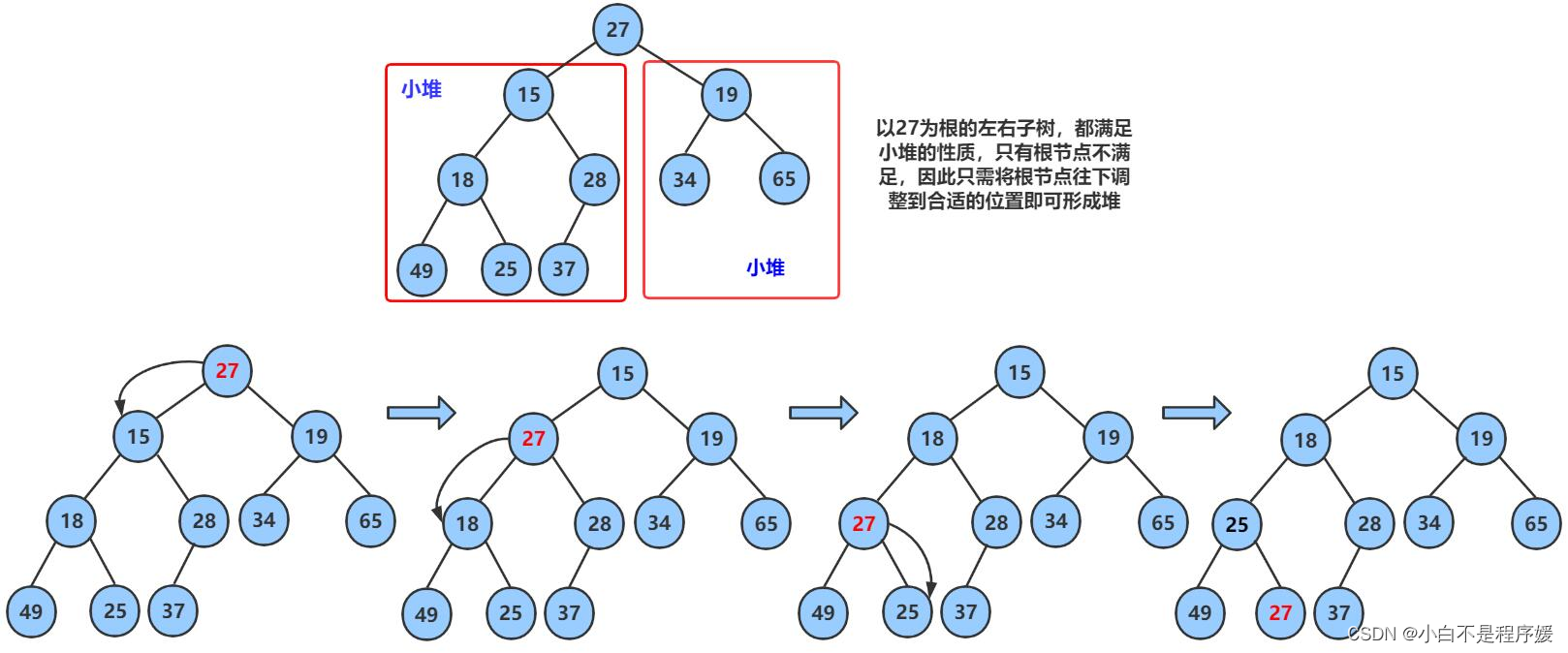
上篇文章我们介绍了向下移动的调整算法,但是这个算法有个前提就是除根外的左右子树都要是堆,但是我们这里给定一个无序数组先让这个数组模拟成堆,除根外左右子树有可能都不是堆,就无法实现向下调整算法,这样我们从倒数第一个非子叶结点开始向下调整也就是最后一个结点的父亲开始向下调整,我们直到数组在空间中是连续的,那我们从这个结点开始没向下调整依次,这个结点向前移动依次这样就将一个大堆分成各个小堆,完成向下调整了。
实现代码
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}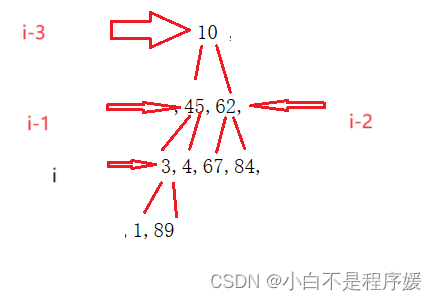
像这样经过多次的向下调整,最终就可以实现堆。
堆排序
在实现堆排序之前我们先思考下升序和降序需要建什么堆?
我们这里直接给出答案:
升序:建大堆
降序:建小堆
问什么会是这样呢?
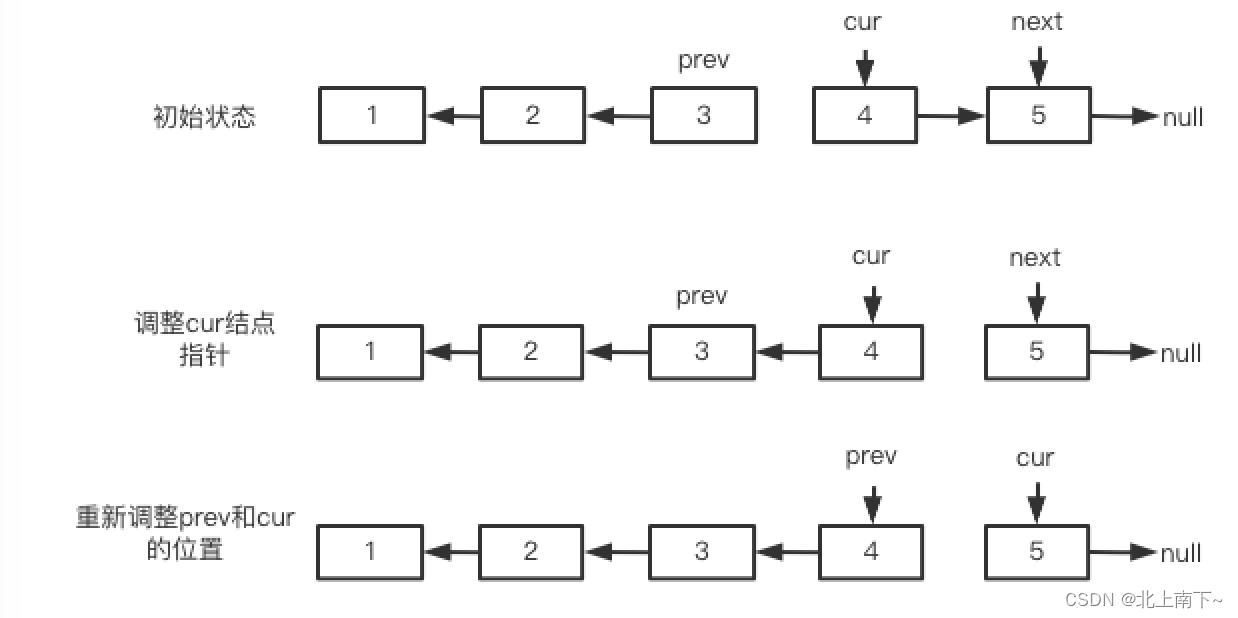
在上篇文章中堆的删除中,我们已经隐含的告诉大家了,如果我们要删除堆中的数据时直接向前移动数据会造成不是原有的大堆或者小堆,因此我们将根结点的数据和最后一个数据交换,两个子树依然是堆然后进行向下调整,size向前移动。我们不做删除这一步是不是就是排序!
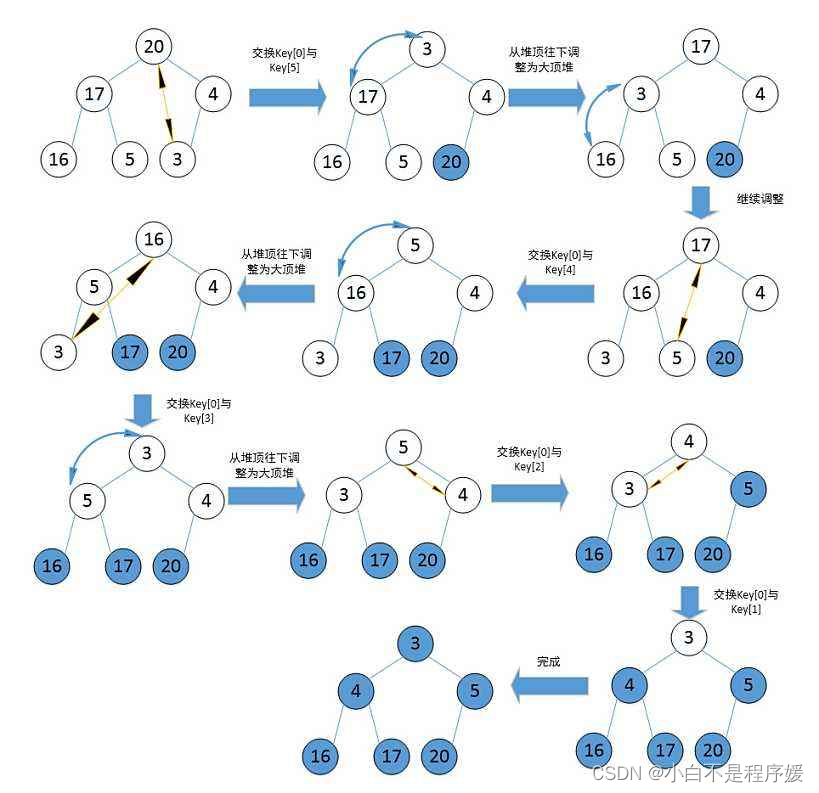
实现代码
int end = n - 1;
while (end > 0)
{
swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
end--;
}TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
void PrintTopK(const char* filename, int k)
{
// 1. 建堆--用a中前k个元素建堆
FILE* fout = fopen(filename, "r");
if (fout == NULL)
{
perror("fopen fail");
return;
}
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror("malloc fail");
return;
}
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &minheap[i]);
}
// 前k个数建小堆
for (int i = (k-2)/2; i >=0 ; --i)
{
AdjustDown(minheap, k, i);
}
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
int x = 0;
while (fscanf(fout, "%d", &x) != EOF)
{
if (x > minheap[0])
{
// 替换你进堆
minheap[0] = x;
// 向下调整算法函数
AdjustDown(minheap, k, 0);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
printf("\n");
free(minheap);
fclose(fout);
}
// fprintf fscanf
void CreateNDate()
{
// 造数据
int n = 10000000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < n; ++i)
{
int x = (rand() + i) % 10000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
int main()
{
//CreateNDate();
PrintTopK("data.txt", 5);
return 0;
}
文件操作知识忘了的话自己回顾下。
今天的内容到这里就结束了,感谢大家的观看!可以在评论区多多交流和探讨,指出我的错误!
下篇文章将讲解完全二叉树的实现!请大家敬请期待!!!