第二十四章原理篇：DBB

上班真的好累哦！
理论上应该从RepVGG开始写重参化的，而且上星期就打算写来着！
但是上班真的好累哦完全提不起精神在周末打字看论文！

参考教程：
https://arxiv.org/pdf/2103.13425.pdf
https://github.com/DingXiaoH/DiverseBranchBlock

文章目录

介绍
原理
- conv-bn => conv
- branch addition => conv
- sequential conv => conv
- depth concatenation=>conv
- avgpooling => conv
- multi-scale conv=>conv
代码实现
- transforms
- - conv-bn => conv
  - branch addition => conv
  - sequential conv => conv
  - depth concatenation=>conv
  - avgpooling => conv
  - multi-scale conv=>conv
- DiverseBranchBlock
- - init
  - get_equivalent_kernel_bias

介绍

diverse branch block，就如同它的名称一样，是一个block形式的设计，这个block有多种分支组合，比如卷积、多尺度卷积、平均池化等。在训练阶段是正常的每个分支都会用到，在inference阶段则会将多分支合并到一起，变成一个卷积层来进行部署，从而实现相对于单卷积层的模型，在参数量不增加的情况下，带来明显的效果提升。

早在inception net时期就已经揭示过多分支结构和不同尺度复杂度支路的组合给模型的特征提取能带来明显效果提升。但是这种复杂的结构，在inference阶段就会显得有点累赘，因为小操作太多了，与gpu的并行计算能力不太匹配，从而速度上会有所下降。

由于业务需要或硬件限制，我们并不能无限地提升我们要训练的卷积网络的大小。在评价一个网络的水平时，一般也会对它的表现、时间损耗和计算量等多方面进行评估。

作者使用重参数化的方法，在卷积网络中插入复杂的模块来提高它的表现能力，同时保证原来的预测时间不会增加。通过“在训练阶段复杂化模型并在预测阶段将它还原”的方法解耦训练时间和预测时间，基于这一目的，对模型修改后的结构做出了以下两个要求：

能够有效提升模型的表现。
能够成功被还原为原结构。

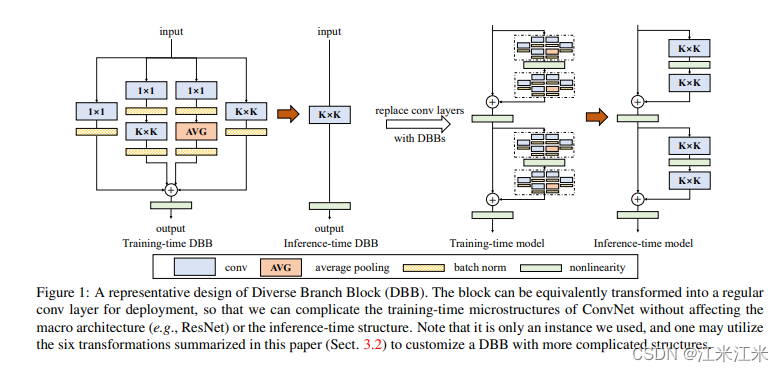
上图是一个dbb结构的示意图，在途中dbbblock使用了四种分支，其中分别包括了1x1卷积，1x1卷积+kxk卷积，1x1卷积+avg池化，kxk卷积。在测试阶段，这四个分支被合并到一起，组成一个kxk的卷积，从而在保证结果的情况下减少参数量。

原理

dbb实现的核心原理是卷积计算的同质性和可加性。

用 $\bigotimes$ 符号代表卷积，那么在两个相同结构的卷积操作上有：
$\bigotimes(pF) = p(I\bigotimes F)\\ I\bigotimes F^{(1)} + I \bigotimes F^{(2)} = I\bigotimes(F^{(1)}+F^{(2)})$
基于这一点，论文中提出来六中转换的情况。
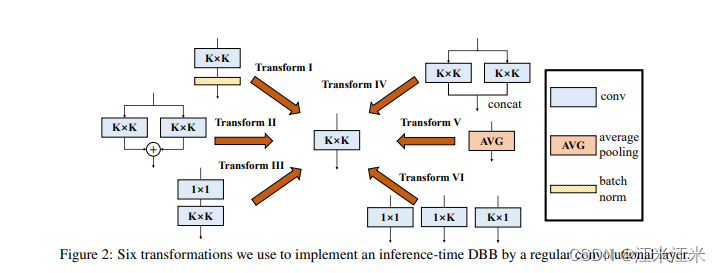
在这里插入图片描述

conv-bn => conv

第一种转换是带bn层的卷积转成普通的卷积。这种转换是很常用的，一个featuremap经过卷积+bn的组合后，得到的输出为：
$\begin{align} O_j &= ((I\bigotimes F_j) - \mu_j)\frac{\gamma_j}{\omicron_j} + \beta_j \\ & = \frac{\gamma_j}{\omicron_j} (I\bigotimes F_j)-\frac{\gamma_j}{\omicron_j}\mu_j + \beta_j \\ &=I \bigotimes(\frac{\gamma_j}{\omicron_j} F_j) -\frac{\gamma_j}{\omicron_j}\mu_j + \beta_j \end{align}$

branch addition => conv

并行的多个结构相同的卷积，根据卷积的可加性，可以直接相加合并到一起。
$I\bigotimes F^{(1)} + I \bigotimes F^{(2)} = I\bigotimes(F^{(1)}+F^{(2)})$

sequential conv => conv

可以把一组连续的1x1卷积-bn-kxk卷积-bn组合成一个kxk卷积。这也是例子中最复杂的一种变换。在这里不考虑组卷积。

首先先按照bn和conv的融合，将1x1卷积，KxK卷积先分别与各自相接的bn融合在一起。
现在我们得到两个卷积层，每一层的滤波器大小分别是
$F^{(1)} \in R^{D\times C\times1\times1}$ 和 $F^{(2)} \in R^{D\times C\times K\times K}$
那么这一层的输出可以写成：
$(I\bigotimes F^{(1)} + REP(b^{(1)}))\bigotimes F^{(2)} + REP(b^{(2)})$
我们的目的是找到一个signle conv，它的kernel和bias满足：
$\bigotimes F' + REP(b')$
我们来续写一下：
$\begin{align} O'&= (I\bigotimes F^{(1)} + REP(b^{(1)}))\bigotimes F^{(2)} + REP(b^{(2)})\\ &=I\bigotimes F^{(1)} \bigotimes F^{(2)} +REP(b^{(1)})\bigotimes F^{(2)} + REP(b^{(2)}) \end{align}$
其中 $F^{(1)}$ 是一个1x1卷积，它只实现了通道上的变化，而没有进行空间上的操作，所以可以通过重组KxK的参数实现两者的合并。

depth concatenation=>conv

inception单元在各分支最后使用concatenation的操作来堆叠组合来自不同分支的结果，假如多个分支的卷积结构相同，那么沿通道拼接结果就等价于把每个分支的卷积核沿通道拼接。

avgpooling => conv

大小为K，stride为s的平均池化，相当于使用了同样的大小为K，步长为s的卷积。只不过这个卷积核的参数是固定的。
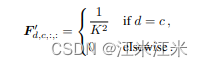
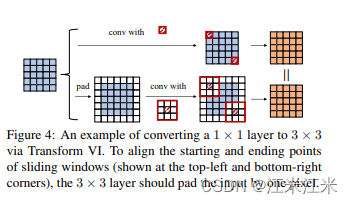
在这里插入图片描述

multi-scale conv=>conv

通过padding的方式来实现不同大小的卷积核的融合。
在这里插入图片描述

代码实现

transforms

参考github源码看一下代码每一种transform是怎么实现的。

conv-bn => conv

实现bn和conv的融合。

def transI_fusebn(kernel, bias, bn):
    gamma = bn.weight
    std = (bn.running_var + bn.eps).sqrt()
    return kernel * ((gamma / std).reshape(-1, 1, 1, 1)), bias + bn.bias - bn.running_mean * gamma / std

和公式里写的一样，直接对参数进行乘法计算。符合卷积的同质性。

branch addition => conv

根据卷积的可加性，直接对多个卷积进行相加即可。

def transII_addbranch(kernels, biases):
    return sum(kernels), sum(biases)

sequential conv => conv

序列卷积的融合：1x1-BN-kxk-BN。我们只写group=1的情况。

def transIII_1x1_kxk(k1, b1,  k2, b2):
	k = F.conv2d(k2, k1.permute(1,0,2,3))
	b_hat = (k2*b1.reshape(1,-1,1,1)).sum((1,2,3))
	return k, b_hat +b2

depth concatenation=>conv

def transIV_depthconcat(kernels, biases):
    return torch.cat(kernels), torch.cat(biases)

avgpooling => conv

def transV_avg(channels, kernel_size, groups):
    input_dim = channels // groups
    k = torch.zeros((channels, input_dim, kernel_size, kernel_size))
    k[np.arange(channels), np.tile(np.arange(input_dim), groups), :, :] = 1.0 / kernel_size ** 2
    return k

multi-scale conv=>conv

def transVI_multiscale(kernel, target_kernel_size):
    H_pixels_to_pad = (target_kernel_size - kernel.size(2)) // 2
    W_pixels_to_pad = (target_kernel_size - kernel.size(3)) // 2
    return F.pad(kernel, [H_pixels_to_pad, H_pixels_to_pad, W_pixels_to_pad, W_pixels_to_pad])

DiverseBranchBlock

DBB类中，比较关键的两个函数：

init() 在init函数中初始化了dbbblock模块，并定义了多个分支，具体来说，这几个分支分别是：dbb_origin, dbb_avg, dbb_1x1和dbb_1x1_kxk。
get_equivalent_kernel_bias(): 在这个函数中进行分支的融合和转换，并获得合并成一个kxk卷积的kernel和bias。

init

我们首先来看一下init中定义的几个分支都是什么样子的结构。

dbb_orgin: 简单的kernel大小为k的卷积+bn

dbb_origin = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=stride, padding=padding, dilation=dilation, groups=groups)

dbb_1x1：简单的kernel大小为1的卷积+bn

self.dbb_1x1 = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=1, stride=stride,padding=0, groups=groups)

dbb_avg：有两种结构
如果group数比out_channels小，则在最开始加上了1x1的组卷积。

self.dbb_avg.add_module('conv', nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=1,stride=1, padding=0, groups=groups, bias=False))
self.dbb_avg.add_module('bn', BNAndPadLayer(pad_pixels=padding, num_features=out_channels))
self.dbb_avg.add_module('avg', nn.AvgPool2d(kernel_size=kernel_size, stride=stride, padding=0))

否则只使用一个平均池化：

self.dbb_avg.add_module('avg', nn.AvgPool2d(kernel_size=kernel_size, stride=stride, padding=0))

最后还要跟上一个bn层。

self.dbb_avg.add_module('avgbn', nn.BatchNorm2d(out_channels))

dbb_1x1_kxk：相对来说比较复杂的卷积序列。

self.dbb_1x1_kxk = nn.Sequential()
if internal_channels_1x1_3x3 == in_channels:
	self.dbb_1x1_kxk.add_module('idconv1', IdentityBasedConv1x1(channels=in_channels, groups=groups))
else:
	self.dbb_1x1_kxk.add_module('conv1', nn.Conv2d(in_channels=in_channels, out_channels=internal_channels_1x1_3x3,
	                                            kernel_size=1, stride=1, padding=0, groups=groups, bias=False))
self.dbb_1x1_kxk.add_module('bn1', BNAndPadLayer(pad_pixels=padding, num_features=internal_channels_1x1_3x3, affine=True))
self.dbb_1x1_kxk.add_module('conv2', nn.Conv2d(in_channels=internal_channels_1x1_3x3, out_channels=out_channels,
                                            kernel_size=kernel_size, stride=stride, padding=0, groups=groups, bias=False))
self.dbb_1x1_kxk.add_module('bn2', nn.BatchNorm2d(out_channels))

在训练阶段，会正常使用这几个分支，并把结果求和。在预测阶段，则需要把分支合并起来。

get_equivalent_kernel_bias

在这个部分，会对多个分支进行合并。

dbb_orgin：合并conv和bn。

这个分支只有简单的conv和bn，可以使用我们transform中第一个方法直接进行合并。

k_origin, b_origin = transI_fusebn(self.dbb_origin.conv.weight, self.dbb_origin.bn)

dbb_1x1：合并1x1卷积和bn。

这个分支是1x1卷积和bn，在合并完成后，还需要把合并后的kernel变成我们预期的大小。

k_1x1, b_1x1 = transI_fusebn(self.dbb_1x1.conv.weight, self.dbb_1x1.bn)
k_1x1 = transVI_multiscale(k_1x1, self.kernel_size)

dbb_1x1_kxk：合并1x1-bn-kxk-bn

这个分支存在两个卷积+bn的组合。在把卷积和对应的bn分别融合后，再进行1x1卷积和3x3卷积串联的组合。

k_1x1_kxk_first, b_1x1_kxk_first = transI_fusebn(k_1x1_kxk_first, self.dbb_1x1_kxk.bn1)
        k_1x1_kxk_second, b_1x1_kxk_second = transI_fusebn(self.dbb_1x1_kxk.conv2.weight, self.dbb_1x1_kxk.bn2)
        k_1x1_kxk_merged, b_1x1_kxk_merged = transIII_1x1_kxk(k_1x1_kxk_first, b_1x1_kxk_first, k_1x1_kxk_second, b_1x1_kxk_second, groups=self.groups)

dbb_avg：进行池化和bn的融合。

池化层在这里要先转换成卷积层，在和bn融合在一起。

k_avg = transV_avg(self.out_channels, self.kernel_size, self.groups)
k_1x1_avg_second, b_1x1_avg_second = transI_fusebn(k_avg.to(self.dbb_avg.avgbn.weight.device), self.dbb_avg.avgbn)

如果在定义的时候，池化层前面还使用了1x1卷积，那么还需要把这个卷积和新的池化层融合在一起。

k_1x1_avg_first, b_1x1_avg_first = transI_fusebn(self.dbb_avg.conv.weight, self.dbb_avg.bn)
            k_1x1_avg_merged, b_1x1_avg_merged = transIII_1x1_kxk(k_1x1_avg_first, b_1x1_avg_first, k_1x1_avg_second, b_1x1_avg_second, groups=self.groups)

最后的相加组合

在多分支结构中，不同分支的结果是通过加法组合在一起的，所以最后还需要一个相加的计算。

return transII_addbranch((k_origin, k_1x1, k_1x1_kxk_merged, k_1x1_avg_merged), (b_origin, b_1x1, b_1x1_kxk_merged, b_1x1_avg_merged))

最终我们得到的是一个大小为kxk的新的卷积和bias。它会直接作为我们新建的卷积层的参数，在部署/预测阶段使用。

kernel, bias = self.get_equivalent_kernel_bias()
        self.dbb_reparam = nn.Conv2d(in_channels=self.dbb_origin.conv.in_channels, out_channels=self.dbb_origin.conv.out_channels,
                                     kernel_size=self.dbb_origin.conv.kernel_size, stride=self.dbb_origin.conv.stride,
                                     padding=self.dbb_origin.conv.padding, dilation=self.dbb_origin.conv.dilation, groups=self.dbb_origin.conv.groups, bias=True)
        self.dbb_reparam.weight.data = kernel
        self.dbb_reparam.bias.data = bias