Problem - E - Codeforces

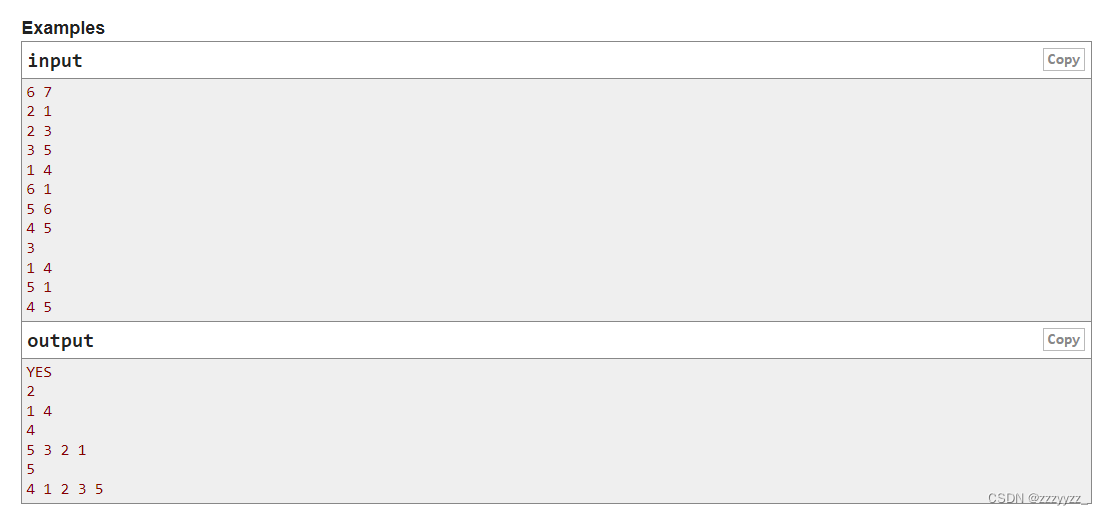
思路：这个题看到之后想到了不可能的情况，就是如果度为奇数就一定不可能实现都是偶数，但是后面就不知道怎么搞了。正解是欧拉定理的应用把算是，首先对于给定的q个要求，我们从a->b连一条边，如果此时生成的图由许多个欧拉回路组成，并且我们还知道给定的这个图是联通的，那么我们就可以生成一颗树，树上的欧拉回路一定会经过每条边两次，所以如果生成的这个图由欧拉回路组成，那么我们一定可以使得每条边经过偶数次，否则如果不由欧拉回路组成，那么就是问我们至少加几条边能够形成欧拉回路，由欧拉回路的条件知道，如果图是联通的，那么如果每个点的度数是偶数，那么这个图一定存在一个欧拉回路，所以现在就变成了加几条便能够使得这个图的每个点的度都是偶数，那么就是找到所有奇数度的顶点数量cnt，那么需要加的变数就是cnt/2条，最后输出路径的时候只需要在建立的树上每次找父节点，类似于最近公共祖先的方法，就可以得到路径。

主要考察了欧拉回路，以及树上的欧拉回路一定会经过每条边两次

// Problem: E. Moment of Bloom
// Contest: Codeforces - Codeforces Round 749 (Div. 1 + Div. 2, based on Technocup 2022 Elimination Round 1)
// URL: https://codeforces.com/contest/1586/problem/E
// Memory Limit: 512 MB
// Time Limit: 3000 ms

#include<bits/stdc++.h>
#include<sstream>
#include<cassert>
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
const double eps=1e-7;
const int N=5e5+7 ,M=1e6+7, INF=0x3f3f3f3f,mod=1e9+7,mod1=998244353;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}

int T,hackT;
int n,m,k;
int d[N];
int h[N],e[M],ne[M],idx;
PII edge[N];
int f[N];
int fa[N];
int depth[N];

void add(int a,int b) {
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

int find(int x) {
	if(x!=f[x]) f[x]=find(f[x]);
	return f[x];
}

void dfs(int u,int father,int dep) {
	fa[u]=father;
	depth[u]=dep;
	for(int i=h[u];i!=-1;i=ne[i]) {
		int j=e[i];
		
		if(j==father) continue;
		dfs(j,u,dep+1); 
	}
}

void get(int a,int b,vector<int> &vis) {
	vector<int> x,y;
	bool flag=false;
	if(depth[a]<=depth[b]) swap(a,b),flag=true;
	
	while(depth[a]!=depth[b]) {
		x.push_back(a);
		a=fa[a];
	}
	
	if(a==b) {
		x.push_back(b);
		if(flag) {
			for(int i=x.size()-1;i>=0;i--) vis.push_back(x[i]);
		}else {
			for(int i=0;i<x.size();i++) vis.push_back(x[i]);
		}
		return ;
	}
	
	while(fa[a]!=fa[b]) {
		x.push_back(a);
		y.push_back(b);
		a=fa[a],b=fa[b];
	}
	
	x.push_back(a);
	y.push_back(b);
	a=fa[a];
	
	if(flag) {
		for(int i=0;i<y.size();i++) vis.push_back(y[i]);
		vis.push_back(a);
		for(int i=x.size()-1;i>=0;i--) vis.push_back(x[i]);
	}else {
		for(int i=0;i<x.size();i++) vis.push_back(x[i]);
		vis.push_back(a);
		for(int i=y.size()-1;i>=0;i--) vis.push_back(y[i]);
	}
}

void solve() {
	n=read(),m=read();
	
	for(int i=1;i<=n;i++) f[i]=i;
	
	memset(h,-1,sizeof h);
	for(int i=1;i<=m;i++) {
		int a=read(),b=read();
		int fa=find(a),fb=find(b);
		
		if(fa!=fb) {
			f[fa]=fb;
			add(a,b),add(b,a);
		}
	}
	
	int q=read();
	for(int i=1;i<=q;i++) {
		edge[i].fi=read(),edge[i].se=read();
		d[edge[i].fi]++;
		d[edge[i].se]++;
	}
	
	int res=0;
	for(int i=1;i<=n;i++) if(d[i]%2==1) res++;
	
	if(res!=0) {
		printf("NO\n");
		printf("%d\n",res/2);
	}else {
		printf("YES\n");
		
		dfs(1,-1,1);
		
		for(int i=1;i<=q;i++) {
			vector<int> vis;
			int a=edge[i].fi,b=edge[i].se;
			get(a,b,vis);
			printf("%d\n",vis.size());
			for(auto &it:vis) printf("%d ",it);
			printf("\n");
		}
	}
}   

int main() {
    // init();
    // stin();
	// ios::sync_with_stdio(false); 

    // scanf("%d",&T);
    T=1; 
    while(T--) hackT++,solve();
    
    return 0;       
}