动态规划DP

news2024/10/6 2:31:24

动态规划 DP

  • 3. 动态规划 DP
    • 什么是动态规划
    • 动态规划和其他算法的区别
    • 解题方法
    • 解题步骤
    • [509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/) (easy)
      • 暴力递归
      • 递归 + 记忆体
      • 动态规划
      • 滚动数组优化
      • 动态规划 + 降维
    • [62. 不同路径](https://leetcode.cn/problems/unique-paths/)(midium)
      • 1. 动态规划
      • 2. 状态压缩
    • [63. 不同路径 II ](https://leetcode.cn/problems/unique-paths-ii/)(midium)
      • 1. 动态规划
      • 2. 状态压缩
    • [70. 爬楼梯](https://leetcode.cn/problems/climbing-stairs/)
      • 思路
      • 1.动态规划
      • 2.状态压缩
      • 3.降维
    • [279. 完全平方数](https://leetcode.cn/problems/perfect-squares/)
      • 思路
      • 方法1:动态规划
    • [120. 三角形最小路径和](https://leetcode.cn/problems/triangle/)
      • 1.动态规划
      • 2.状态压缩

3. 动态规划 DP

什么是动态规划

动态规划，英文：Dynamic Programming，简称DP，将问题分解为互相重叠的子问题，通过反复求解子问题来解决原问题就是动态规划，如果某一问题有很多重叠子问题，使用动态规划来解是比较有效的。

Q:什么是重叠子问题

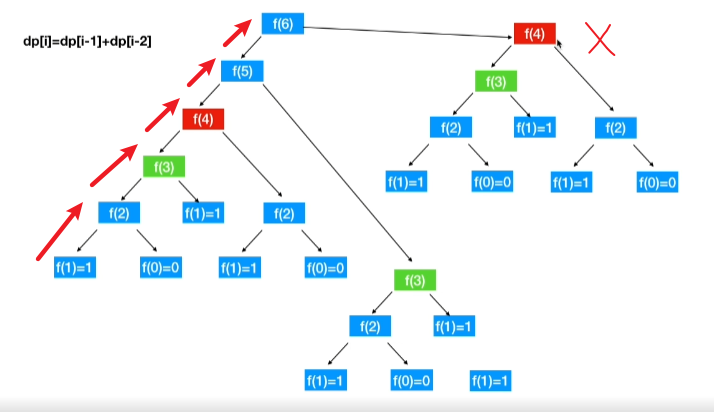
A:比如这里要求的f(4) f(3) … f(1)就是重叠子问题

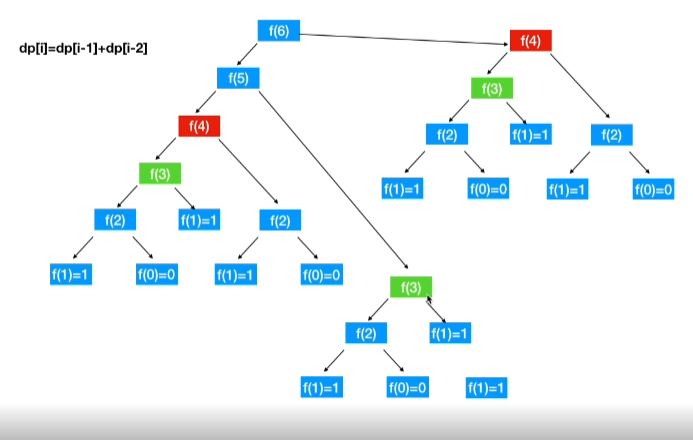
image-20221219015225017

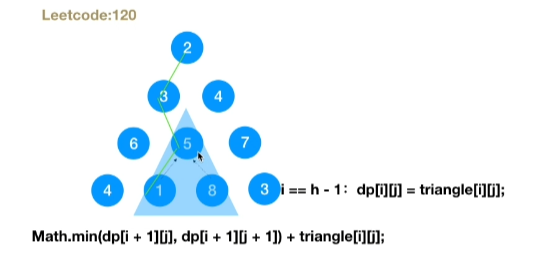
求解动态规划的核心问题是穷举，但是这类问题穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下。动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。另外，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出**正确的「状态转移方程」**才能正确地穷举。重叠子问题、最优子结构、状态转移方程就是动态规划三要素

Q:什么是最优子结构?

A:问题寻找从顶部到底部相加和最小的路径,现在已经在5这个位置,可以向1和8走,显然5+1比5+8小,那么5往1走就是最优的子结构

image-20221219015537608

动态规划和其他算法的区别

  1. 动态规划和分治的区别：动态规划和分治都有最优子结构 ，但是分治的子问题不重叠
    分治没有重复的子问题
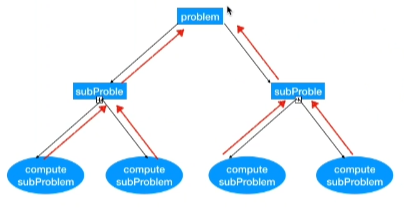
    image-20221219020103735
  2. 动态规划和贪心的区别：动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优解，所以它永远是局部最优，但是全局的解不一定是最优的。
    比如
    image-20221219020250267
  3. 动态规划和递归的区别：递归和回溯可能存在非常多的重复计算，动态规划可以用递归加记忆化的方式减少不必要的重复计算

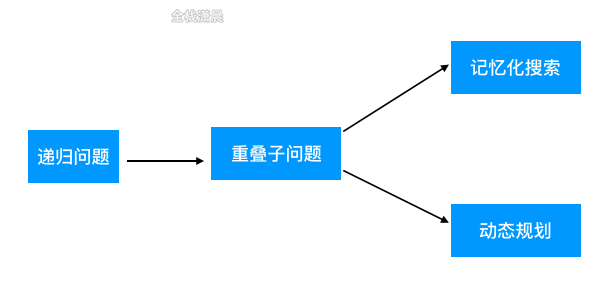
解题方法

  • 递归+记忆化(自顶向下)
  • 动态规划（自底向上）

ds_135

解题步骤

  1. 根据重叠子问题定义状态
  2. 寻找最优子结构推导状态转移方程
  3. 确定dp初始状态
  4. 确定输出值

509. 斐波那契数 (easy)

  1. dp(n) 表示第n个位置斐波那契数为多少
  2. 状态转移方程 dp(n) = dp(n-1) + dp(n-2)
  3. dp初始状态 dp(0) = 0 dp(1) = 1
  4. 确定输出值

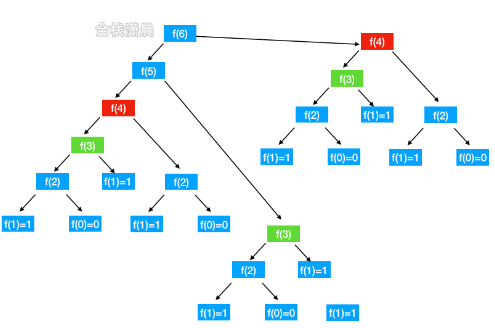
image-20221219020720124

暴力递归

class Solution {
    public int fib(int n) {
        if (n == 0) {
            return 0;
        } else if (n == 1) {
            return 1;
        }

        return fib(n - 1) + fib(n - 2);
    }
}

image-20221219021847649

递归 + 记忆体

也就是自顶向下

class Solution {
    //用于存储已经计算过的值
    static HashMap<Integer,Integer> hashMap = new HashMap<>();
    public int fib(int n) {
        //如果已经计算过,直接返回结果
        if(hashMap.containsKey(n)){
            return hashMap.get(n);
        }


        if (n == 0) return 0;
        if (n == 1) return 1;
		
        //计算完后放入HashMap
        hashMap.put(n,fib(n - 1) + fib(n - 2));
        return hashMap.get(n);
    }
}

image-20221219022309266

动态规划

沿着一条路往上走,不会去走其他路了

image-20221219023335258

class Solution {
    static int[] dp = new int[50];
    public int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        dp[0] = 0;
        dp[1] = 1;
        
        for (int i = 2; i <= n; i++) {
            //自底向上计算每个状态
            dp[i] = dp[i-1] + dp[i-2];
        }

        return dp[n];
    }
}

image-20221219023434418

滚动数组优化

因为每个斐波那契数只与前两个斐波那契数有关,所以其实可以把数组的长度设为3或2,优化空间复杂度

class Solution {
    static int[] dp = new int[3];
    public int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            //自底向上计算每个状态
            dp[2] = dp[0] + dp[1];

            //数组滚动
            dp[0] = dp[1];
            dp[1] = dp[2];

        }

        return dp[2];
    }
}

//再次优化,把数组变为2

class Solution {
    static int[] dp = new int[2];
    public int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        dp[0] = 0;
        dp[1] = 1;
        int sum = 0;

        for (int i = 2; i <= n; i++) {
            //自底向上计算每个状态
            sum = dp[0] + dp[1];

            //数组滚动
            dp[0] = dp[1];
            dp[1] = sum;
        }

        return sum;
    }
}

image-20221219024331099

动态规划 + 降维

降维能减少空间复杂度，但不利于程序的扩展

比如如果我们要获取过程中的每一个斐波那契数,这种方法就不好扩展了

class Solution {
    public int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        int prev0 = 0;
        int prev1 = 1;
        int sum = 0;
        for (int i = 2; i <= n; i++) {
            //自底向上计算每个状态
            sum = prev0 + prev1;
            prev0 = prev1;
            prev1 = sum;

        }

        return sum;
    }
}

image-20221219024833175

  • 思路：自底而上的动态规划
  • 复杂度分析：时间复杂度O(n)，空间复杂度O(1)

62. 不同路径(midium)

难度中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

img

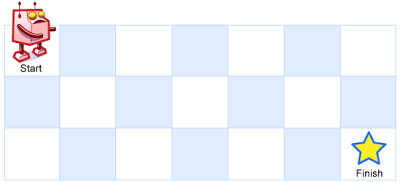
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

  • 1 <= m, n <= 100
  • 题目数据保证答案小于等于 2 * 109

1. 动态规划

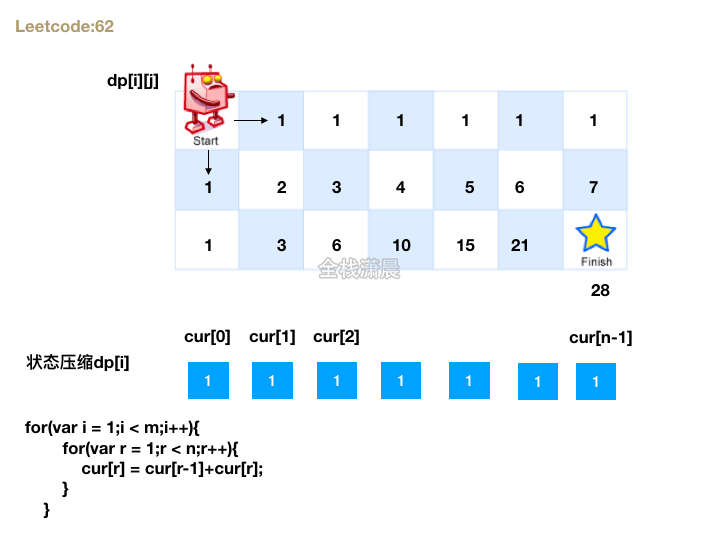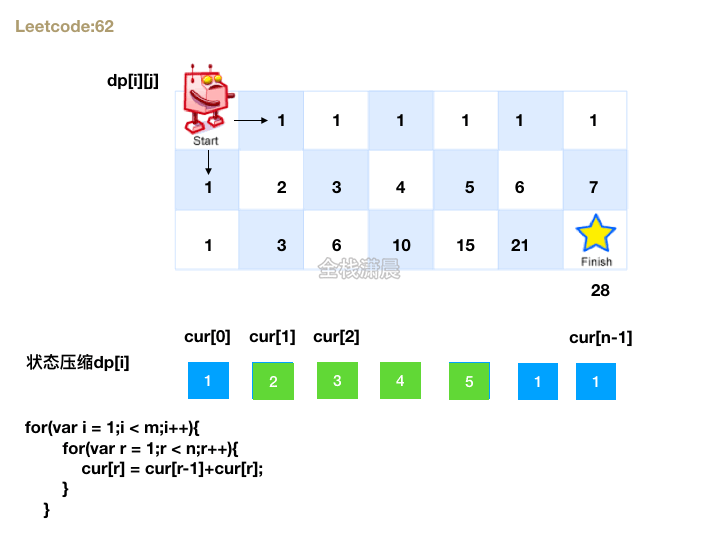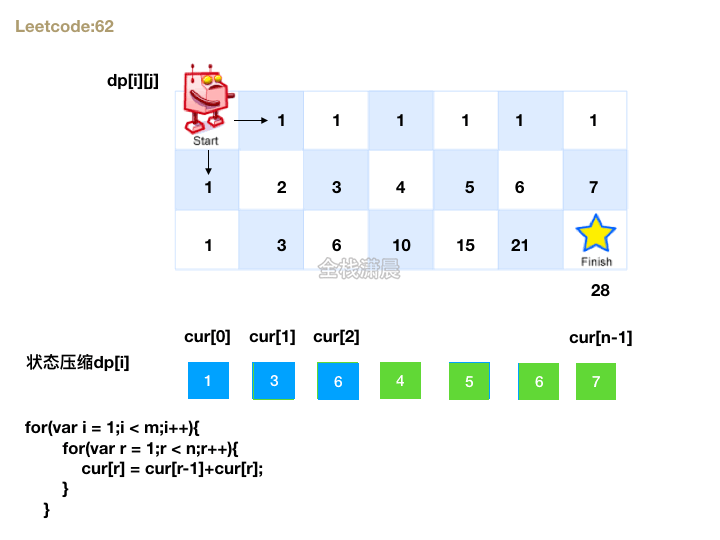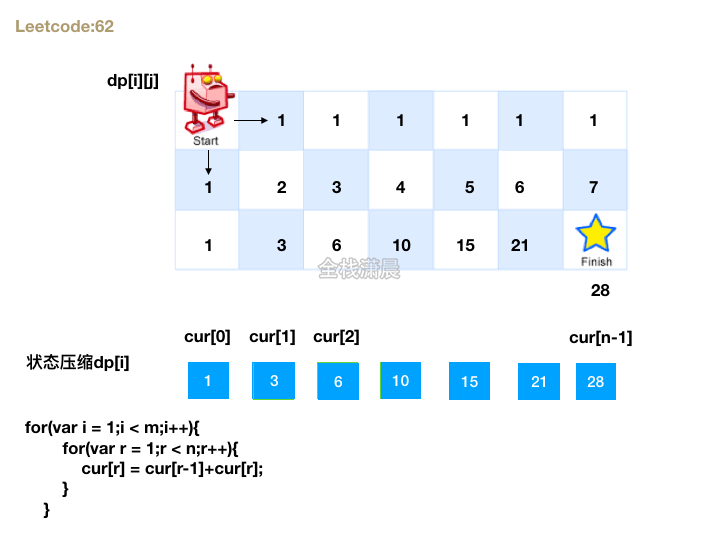
123133
  1. 根据重叠子问题定义状态
    • dp[i][j]表示到达i j的位置有多少种路径
  2. 寻找最优子结构推导状态转移方程
    • 由于在每个位置只能向下或者向右， 所以每个坐标的路径和等于上一行相同位置和上一列相同位置不同路径的总和，状态转移方程：dp[i][j] = dp[i-1][j] + dp[i][j-1];
  3. 确定dp初始状态
    • dp[0][0...n] = 1
    • dp[0...m][0] = 1
  4. 确定输出值
  • 复杂度:时间复杂度O(mn)。空间复杂度O(mn)，优化后空间复杂度O(n)
class Solution {
    public int uniquePaths(int m, int n) {
        //定义状态
        int[][] dp = new int[m][n];
        //初始化
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                //状态转移方程
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
}

image-20221219032424862

2. 状态压缩

123133
  1. 可以先建一个都是1的一维数组表示第一行
  2. 我们注意到2这个位置是左边加上上边的和
    • 左边就是数组中的前一位
    • 上边其实就是自己的值
  3. 自己等于自己加上左边
class Solution {
    public int uniquePaths(int m, int n) {
        //定义状态
        int[] dp = new int[n];
        //初始化
        Arrays.fill(dp, 1);

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                //状态转移方程
                dp[j] = dp[j] + dp[j-1];
            }
        }

        return dp[n-1];
    }
}

image-20221219032353292

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        //1. 根据重叠子问题定义状态
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int dp[][] = new int[m][n];
        //2. 确定dp初始状态
        //上边和左边都是1
        for (int i = 0; i < m; i++) {
            //不是障碍物才填1
            if(obstacleGrid[i][0] != 1){
                dp[i][0] = 1;
            }else {
                break;
            }
        }
        for (int i = 0; i < n; i++) {
            //不是障碍物才填1
            if(obstacleGrid[0][i] != 1){
                dp[0][i] = 1;
            }else {
                break;
            }
        }


        //3. 寻找最优子结构推导状态转移方程
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                //如果是障碍物
                if(obstacleGrid[i][j] == 1){
                    dp[i][j] = 0;
                    continue;
                }
                //不是障碍物 dp[i][j] = dp[i-1][j] + dp[i][j-1]
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

63. 不同路径 II (midium)

难度中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

img

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

img

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

  • m == obstacleGrid.length

  • n == obstacleGrid[i].length

  • 1 <= m, n <= 100

  • obstacleGrid[i][j] 为 0 或 1

  • 思路：和62题一样，区别就是遇到障碍直接返回0

  • 复杂度：时间复杂度O(mn)，空间复杂度O(mn)，状态压缩之后是o(n)

1. 动态规划

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        //1. 根据重叠子问题定义状态
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int dp[][] = new int[m][n];
        //2. 确定dp初始状态
        //上边和左边都是1,遇到障碍物开始后面都是0
        for (int i = 0; i < m; i++) {
            //不是障碍物填1
            if(obstacleGrid[i][0] != 1){
                dp[i][0] = 1;
            }else {
                //遇到障碍物返回
                break;
            }
        }
        for (int i = 0; i < n; i++) {
            //不是障碍物填1
            if(obstacleGrid[0][i] != 1){
                dp[0][i] = 1;
            }else {
                //遇到障碍物返回
                break;
            }
        }


        //3. 寻找最优子结构推导状态转移方程
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                //如果是障碍物
                if(obstacleGrid[i][j] == 1){
                    dp[i][j] = 0;
                    continue;
                }
                //不是障碍物 dp[i][j] = dp[i-1][j] + dp[i][j-1]
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

image-20221220022609385

2. 状态压缩

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        //1. 根据重叠子问题定义状态
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int dp[] = new int[n];
        //2. 确定dp初始状态
        dp[0] = obstacleGrid[0][0] == 1 ? 0 : 1; 
		//dp[0] = 1; //也可以直接先用1填充,因为后面会遍历到
        
        
        //3. 寻找最优子结构推导状态转移方程
        //注意这里从0开始
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                //遇到障碍物
                if(obstacleGrid[i][j] == 1){
                    dp[j] = 0;
                    continue;
                }
                //最左边的时候.左边没有元素
                if(j >= 1){
                    dp[j] = dp[j] + dp[j-1];
                }
                //等于上边(自己)和左边的和
            }
        }

        return dp[n-1];
    }
}

image-20221220023721317

70. 爬楼梯

难度简单

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

  • 1 <= n <= 45

思路

  • 思路：因为每次可以爬 1 或 2 个台阶，所以到第n阶台阶可以从第n-2或n-1上来，其实就是斐波那契的dp方程
  • 复杂度分析：时间复杂度O(n)，空间复杂度O(1)

1.动态规划

当前台阶可以由前一个台阶走过来,也可以由前两个台阶走过来

所以走法数 = 前一个台阶走法数 + 前两个台阶走法数

ds_71

class Solution {
    public int climbStairs(int n) {

        if(n == 1){
            return 1;
        }

        //1.定义状态
        int[] dp = new int[n];

        //2.初始化
        dp[0] = 1;
        dp[1] = 2;

        //3.状态转移方程
        for (int i = 2; i < n; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }

        return dp[n-1];
    }
}

image-20221220025746581

2.状态压缩

class Solution {
    public int climbStairs(int n) {

        if (n == 1) {
            return 1;
        } else if (n == 2) {
            return 2;
        }

        //1.定义状态
        int[] dp = new int[2];

        //2.初始化
        dp[0] = 1;
        dp[1] = 2;
        int result = 0;

        //3.状态转移方程
        for (int i = 2; i < n; i++) {
            result = dp[0] + dp[1];
            dp[0] = dp[1];
            dp[1] = result;
        }

        return result;
    }
}

image-20221220030243281

3.降维

class Solution {
    public int climbStairs(int n) {

        if (n == 1) {
            return 1;
        } else if (n == 2) {
            return 2;
        }

        //1.定义状态
        //2.初始化
        int prev1 = 1;
        int prev2 = 2;
        int result = 0;

        //3.状态转移方程
        for (int i = 2; i < n; i++) {
            result = prev1 + prev2;
            prev1 = prev2;
            prev2 = result;
        }

        return result;
    }
}

279. 完全平方数

难度中等

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

  • 1 <= n <= 104

思路

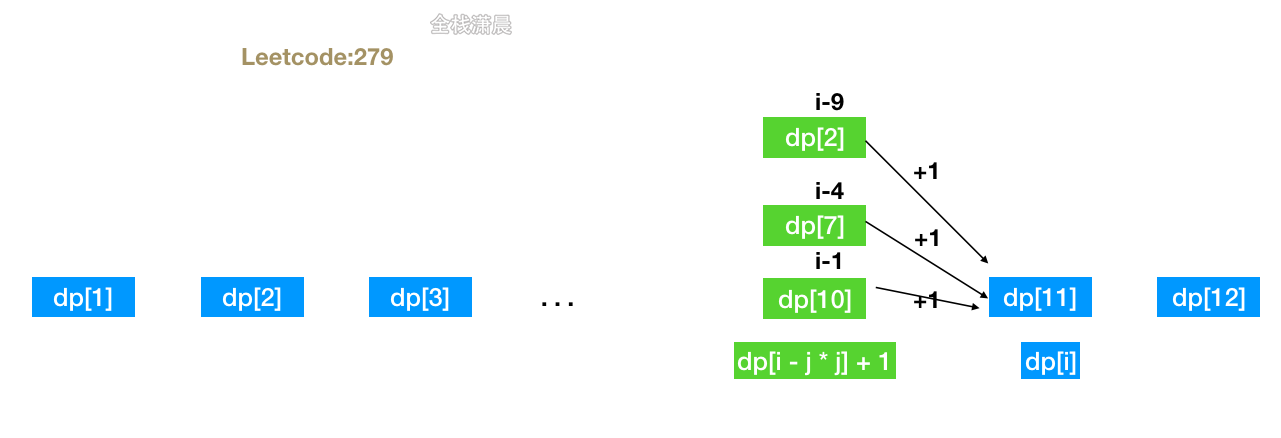
ds_204

dp[i] 的i减去所有比i小的完全平方数的平方 dp[i- j * j]

然后再+1,比较dp[i]和dp[i- j * j] + 1得到小的那个

方法1:动态规划

  • 思路：dp[i] 表示i的完全平方和的最少数量，dp[i - j * j] + 1表示减去一个完全平方数j的完全平方之后的数量加1就等于dp[i]，只要在dp[i], dp[i - j * j] + 1中寻找一个较少的就是最后dp[i]的值。

  • 复杂度：时间复杂度O(n* sqrt(n))，n是输入的整数，需要循环n次，每次计算dp方程的复杂度sqrt(n)，空间复杂度O(n)

class Solution {
    public int numSquares(int n) {
        //1.定义状态
        int[] dp = new int[n + 1];

        for (int i = 1; i <= n; i++) {
            //2.初始化 表示都由1这个完全平方数组成
            dp[i] = i;
            for (int j = 1; i - j * j >= 0; j++) {
                //3.状态转移方程
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }

        return dp[n];
    }
}

image-20221220032253897

120. 三角形最小路径和

难度中等

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

提示：

  • 1 <= triangle.length <= 200
  • triangle[0].length == 1
  • triangle[i].length == triangle[i - 1].length + 1
  • -104 <= triangle[i][j] <= 104

进阶：

  • 你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题吗？

ds_72

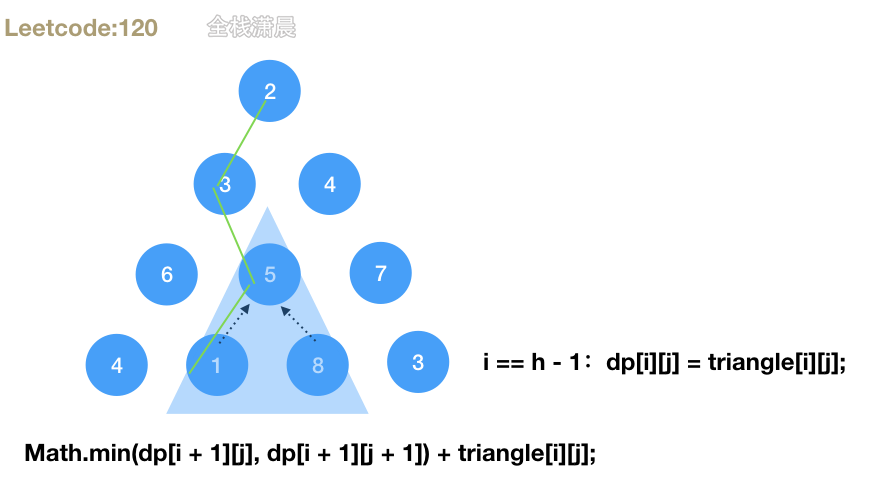
  • 思路：从三角形最后一层开始向上遍历，每个数字的最小路径和是它下面两个数字中的较小者加上它本身
  • 复杂度分析：时间复杂度O(n^2)，空间复杂O(n)

1.动态规划

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        //1. 定义状态
        int n = triangle.size();
        //表示从底部到nn位置的路径长度
        int dp[][] = new int[n][n];

        //2. 初始化
        for (int i = 0; i < n; i++) {
            //获取三角形最后一行
            dp[n-1][i] = triangle.get(n-1).get(i);
        }

        //3. 状态转移方程
        //每个数字的最小路径和是它下面两个数字中的较小者加上它本身
        //从倒数第2层开始
        for (int i = n-2; i >= 0; i--) {
            //第几层就有有多少个元素
            for (int j = 0; j <= i; j++) {
                dp[i][j] = triangle.get(i).get(j) + Math.min(dp[i+1][j] , dp[i+1][j+1]);
            }
        }

        return dp[0][0];
    }
}

image-20221220035808817

2.状态压缩

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        //1. 定义状态
        int n = triangle.size();
        int dp[] = new int[n];

        //2. 初始化
        for (int i = 0; i < n; i++) {
            //获取三角形最后一行
            dp[i] = triangle.get(n-1).get(i);
        }

        //3. 状态转移方程
        //每个数字的最小路径和是它下面两个数字中的较小者加上它本身
        //从倒数第2层开始
        for (int i = n-2; i >= 0; i--) {
            //第几层就有有多少个元素
            for (int j = 0; j <= i; j++) {
                dp[j] = triangle.get(i).get(j) + Math.min(dp[j] , dp[j+1]);
            }
        }

        return dp[0];
    }
}

image-20221220035039633

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/102340.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[vue应用实践]：vue3使用自定义指令定义拖拽方法

[vue应用实践]：vue3使用自定义指令定义拖拽方法

总结一些日常需要用到的一些api&#xff0c;也是在一些面试中会经常出现的题目&#xff0c;今天分享的是vue3中使用自定义指令封装拖拽方法&#xff0c; 同时文章也被收录到我的《JS基础》专栏中&#xff0c;欢迎大家点击收藏加关注。 vue指令 vue中有内置的一些指令供我们使用…
阅读更多...
信贷产品年终总结之贷中行为分析

信贷产品年终总结之贷中行为分析

番茄知识星球平台上周开始推出信贷业务年终总结的系列文章&#xff0c;首篇主题为客户特征画像&#xff0c;并已在平台发布&#xff08;12月13日&#xff09;&#xff0c;感兴趣童鞋可前翻查阅。作为系列专题的续集&#xff0c;本篇将围绕信贷存量数据为大家带来第二个主题“贷…
阅读更多...
多维数据库概念与理解

多维数据库概念与理解

如今多维数据库已经越来越普及&#xff0c;不少公司开始研发属于自己公司的基于多维开发的作业平台。利用多维的数据直观化、效率高等优势&#xff0c;直接打开数据分析的大门。 有人好奇什么是多维数据库&#xff1f;下面我和大家一一探讨 其实多维数据库是指将数据存放在一…
阅读更多...
C语言数组

C语言数组

1、数组 数组使用之前必须声明&#xff1a; 类型定义符 数组名[常量表达式] 在声明数组时必须说明数组长度。 较好的方法是用宏来定义数组的长度。 #include <stdio.h> #define N 10 int main() { int arr[N];for(int i0;i<10;i){arr[i]i1;printf("%d &q…
阅读更多...
科技云报道：疫情三年，数字会展成色几何？

科技云报道：疫情三年，数字会展成色几何？

科技云报道原创。 三年疫情&#xff0c;会展行业并未消极等待&#xff0c;线上线下融合趋势越来越明显&#xff0c;“数字展会”模式已成为常态化。 据《中国会展主办机构数字化调研报告&#xff08;2022&#xff09;》显示&#xff0c;超七成会展主办方采取数字化手段提升展…
阅读更多...
OpenCV 之 图像平滑

OpenCV 之 图像平滑

1 图像平滑 图像平滑&#xff0c;可用来对图像进行去噪 (noise reduction) 或 模糊化处理 (blurring)&#xff0c;实际上图像平滑仍然属于图像空间滤波的一种 (低通滤波) 既然是滤波&#xff0c;则图像中任一点 (x, y)&#xff0c;经过平滑滤波后的输出 g(x, y) 如下&#xff…
阅读更多...
从编程小白到年薪40万，为什么首选Python？

从编程小白到年薪40万，为什么首选Python？

前言 在众多的计算及语言中&#xff0c;呼声很高、位列编程语言榜前面的无疑是生命力顽强的java、最近热度猛增的Python、被称为万物之源的C语言、争议很大的PHP等等。但是对于初学者来说&#xff0c;计算机语言就像天书&#xff0c;不知道到底该学习哪个&#xff0c;从哪一门…
阅读更多...
Karl Guttag：Niantic户外AR参考设计或采用Lumus光波导

Karl Guttag：Niantic户外AR参考设计或采用Lumus光波导

前不久&#xff0c;Niantic在高通骁龙峰会上公布了一款用于户外场景的AR眼镜参考设计&#xff0c;其特点是采用无线一体化设计&#xff0c;配备了柔性头带&#xff0c;可用来玩LBS AR游戏。目前关于该AR眼镜方案的信息不多&#xff0c;它的光学方案是大家非常关注的一点&#x…
阅读更多...
游戏服务端 - AOI九宫格算法

游戏服务端 - AOI九宫格算法

游戏服务端 - AOI九宫格算法 下面简述内容&#xff0c;只针对平面上的简易场景。我们将平面上的场景分为一个个格子&#xff08;Grid&#xff09;&#xff0c;场景管理所有的Grid。如下&#xff08;假设场景的长宽均为20&#xff0c;每个格子宽高定义为1&#xff09;&#xff1…
阅读更多...
电脑怎么查看是固态硬盘还是机械硬盘

电脑怎么查看是固态硬盘还是机械硬盘

前言 前两天有粉丝问我&#xff0c;买电脑的时候有的参数看不懂&#xff0c;比如固态硬盘和机械硬盘区分&#xff0c;他听商家说给他配置的电脑是512G固态硬盘&#xff0c;但是又不知道从哪里看到底是不是固态硬盘&#xff0c;怕以次充好。 今天我就跟大家详细介绍一下硬盘到…
阅读更多...
五、path路径模块和url模块

五、path路径模块和url模块

上一篇内容讲到的fs文件系统模块是官方提供的内置模块&#xff0c;本篇path路径模块也是Node.js官方提供的内置模块&#xff0c;也是核心模块&#xff0c;用来处理路径&#xff0c;path模块用来满足用户对路径的处理需求。在上一篇内容就涉及到路径拼接的问题&#xff0c;来一个…
阅读更多...
1 数据结构 绪论（时间空间复杂度）

1 数据结构 绪论（时间空间复杂度）

文章链接是我的掘金博客&#xff0c;大家有兴趣可以去我的博客上看 博客地址&#xff1a;数据结构专栏 1 数据结构 绪论&#xff08;时间空间复杂度&#xff09;考纲要求 &#x1f495;1 术语&#xff08;逻辑结构&存储结构&#xff09;1.1 数据结构的形式定义&#xff08;…
阅读更多...
【图像分割】遗传算法优化K聚类图像分割【含Matlab源码 1605期】

【图像分割】遗传算法优化K聚类图像分割【含Matlab源码 1605期】

⛄一、遗传算法优化K聚类简介 文中提出基于优化遗传算法的模糊聚类图像分割算法, 是在上述对遗传算法进行了优化的基础上形成的。不仅根据个体适应度大小和变化快慢自适应调节变异率和交叉率, 提高计算准确性和效率, 另外, 在遗传算法迭代计算中加入基于曲线二阶导数的约束条件…
阅读更多...
JavaWeb框架（三）：JavaWeb项目实战 基于Servlet 实现系统登录注册功能

JavaWeb框架（三）：JavaWeb项目实战 基于Servlet 实现系统登录注册功能

MVC实战项目 仓储管理系统需求&#xff1a;实现基本的登录和注册功能MVC实战项目&#xff1a;登录和注册登录功能实现注册功能实现总结Redis章节复习已经过去&#xff0c;新的章节JavaWeb开始了&#xff0c;这个章节中将会回顾JavaWeb实战项目 公司管理系统部分功能 代码会同步…
阅读更多...
「地表最强」C++核心编程（四）类和对象--继承

「地表最强」C++核心编程（四）类和对象--继承

环境&#xff1a; 编译器&#xff1a;CLion2021.3&#xff1b;操作系统&#xff1a;macOS Ventura 13.0.1 文章目录一、继承的基本语法二、继承方式2.1 public继承2.2 protected继承2.3 private继承2.4 继承规则三、继承中的对象模型四、继承中的构造和析构顺序五、继承同名成员…
阅读更多...
PyQt5利用Qt designer(QT设计师)使用tab widget和stacked widget实现多页面切换

PyQt5利用Qt designer(QT设计师)使用tab widget和stacked widget实现多页面切换

PyQt5 Qt designer QT设计师 使用tab widget和stacked widget实现多页面切换一、使用Qt designer(QT设计师)进行多页面切换ui设计二、实现tab widget多页面切换三、实现stacked widget多页面切换四、生成代码五、运行效果一、使用Qt designer(QT设计师)进行多页面切换ui设计 本…
阅读更多...
Go 实现线性查找算法和二分查找算法

Go 实现线性查找算法和二分查找算法

耐心和持久胜过激烈和狂热。 哈喽大家好&#xff0c;我是陈明勇&#xff0c;今天分享的内容使用 Go 实现线性查找算法和二分查找算法。如果本文对你有帮助&#xff0c;不妨点个赞&#xff0c;如果你是 Go 语言初学者&#xff0c;不妨点个关注&#xff0c;一起成长一起进步&…
阅读更多...
雪花算法原理

雪花算法原理

SnowFlake算法生成id的结果是一个64bit大小的整数&#xff0c;它的结构如下图&#xff1a;1bit&#xff0c;不用&#xff0c;因为二进制中最高位是符号位&#xff0c;1表示负数&#xff0c;0表示正数。生成的id一般都是用整数&#xff0c;所以最高位固定为0。41bit时间戳&#…
阅读更多...
热门技术中的应用：云计算中的网络-第27讲-云中的网络QoS：邻居疯狂下电影，我该怎么办？

热门技术中的应用：云计算中的网络-第27讲-云中的网络QoS：邻居疯狂下电影，我该怎么办？

在小区里面，是不是经常有住户不自觉就霸占公共通道，如果你找他理论，他的话就像一个相声《楼道曲》说的一样：“公用公用，你用我用，大家都用，我为什么不能用？”。 除此之外，你租房子的时候，有没有碰到这样的情况：本来合租共享WiFi，一个人狂下小电影，从而你网都上不…
阅读更多...
编程15年40岁程序员的我终于在压力下被迫转行了

编程15年40岁程序员的我终于在压力下被迫转行了

本人今年40岁多了&#xff0c;中山大学计算机小硕&#xff0c;已经从事it工作15年多&#xff0c;最后一次工作是2017年&#xff0c;创业&#xff0c;互联网教育方向&#xff0c;2020年失败关闭公司。 创业失败后&#xff0c;在家沉淀了几个月&#xff0c;然后决定再次找工作。…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023