文章链接是我的掘金博客,大家有兴趣可以去我的博客上看
博客地址:数据结构专栏
1 数据结构 绪论(时间空间复杂度)
- 考纲要求 💕
- 1 术语(逻辑结构&存储结构)
- 1.1 数据结构的形式定义(语法格式)✨
- 1.2 数据类型 (抽象数据类型)
- ❗1.2.1 抽象数据类型 (ADT) ❤️✨💕
- ADT的表示和实现💘🆚💬
- 1.3 数据结构的三要素(逻辑、存储、运算)✨💕
- ❗ 1.3.1 逻辑结构
- 结构图:✨
- 逻辑结构的四大分类:✨
- ❗ 1.3.2 存储结构
- 顺序存储结构 ( ..数组)
- 链式存储结构 (...链表)
- 索引存储结构
- 散列存储结构
- 总结:
- 1.3.3 数据运算
- 2. 时间空间复杂度(算法)
- 2.1 算法基本概念和评价
- ❗❗ 2.2 时间空间复杂度✨
- 2.2.1❗❗时间复杂度✨✨
- 推导出大O的方法:
- 1. 常数阶 O(1)
- 2.线性阶
- 3.对数阶
- 4. 平方阶
- 递归时候情况
- 5.线性对数阶O(nlogN)
- 2.2.2 ❗❗最坏\最好\平均时间复杂度✨✨
- 2.2.3 ✨ 空间复杂度
- 变量—O(1)
- 数组—O(n)
- 二维数组 0(n^2)
- 递归
考纲要求 💕
(一)绪论:
1.熟悉各名词、术语的含义,掌握基本概念,特别是数据的逻辑结构和存储结构之间的关系;
2.了解抽象数据类型的定义、表示和实现方法;
3.熟悉类C语言的书写规范,特别要注意值调用和引用调用的区别,输入、输出的方式以及错误处理方式;
4.理解算法五个要素的确切含义;
5.掌握计算语句频度和估算算法时间复杂度的方法。
第一章的主要是理论知识,但是也要基本了解,时间空间复杂度可能会出计算题
1 术语(逻辑结构&存储结构)
如下面思维导图:

关于数据,数据元素、对象等 数据结构的元素构成部分见 文章链接
1.1 数据结构的形式定义(语法格式)✨

1.2 数据类型 (抽象数据类型)
数
据
类
型
\color{#4285f4}{数}\color{#ea4335}{据}\color{#fbbc05}{类}\color{#4285f4}{}\color{#34a853}{}\color{#ea4335}{型}
数据类型:是一个值的集合和定义在此集合上的一组操作的总称
- 原子类型 \color{blue}{原子类型} 原子类型:其值不可再分的数据类型
- 结构类型 \color{blue}{结构类型} 结构类型:其值可以再分解为若干分量的数据类型
- 抽象数据类型 \color{blue}{抽象数据类型} 抽象数据类型 :↓ 1.2.1
比如C++中的bool类型就是原子类型,其值为true或false,所对应的操作可以有与、或、非等
比如C语言中的结构体struct是一种结构类型
struct Coordinate
{
int x;//横坐标
int y://纵坐标
}
其值可以再分,比如这个分为x和y 子量, 所对应的操作可以有赋值等
❗1.2.1 抽象数据类型 (ADT) ❤️✨💕
抽象数据类型 \color{red}{抽象数据类型} 抽象数据类型: 是指具有一定关系的 数据对象集 \color{#03c5fc}{数据对象集} 数据对象集以及定义在该集合上的 一组操作 \color{#03c5fc}{一组操作} 一组操作。
作用:抽象数据类型可以使我们更容易描述现实世界。例:用线性表描述学生成绩表,用树或图描述遗传关系。
定义:一个数学模型以及定义在该模型上的一组操作。
关键:使用它的人可以只关心它的逻辑特征,不需要了解它的存储方式。定义它的人同样不必要关心它如何存储。
ADT的表示和实现💘🆚💬
ADT的表示格式不统一,我们采用下面的格式 :
ADT抽象数据类型名 {
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>

比如下面例子:
数据元素D,数据关系S ,最后P是下面的基本操作

有点类似抽象类,就是存储函数,这个也是数据结构+操作集
1.3 数据结构的三要素(逻辑、存储、运算)✨💕
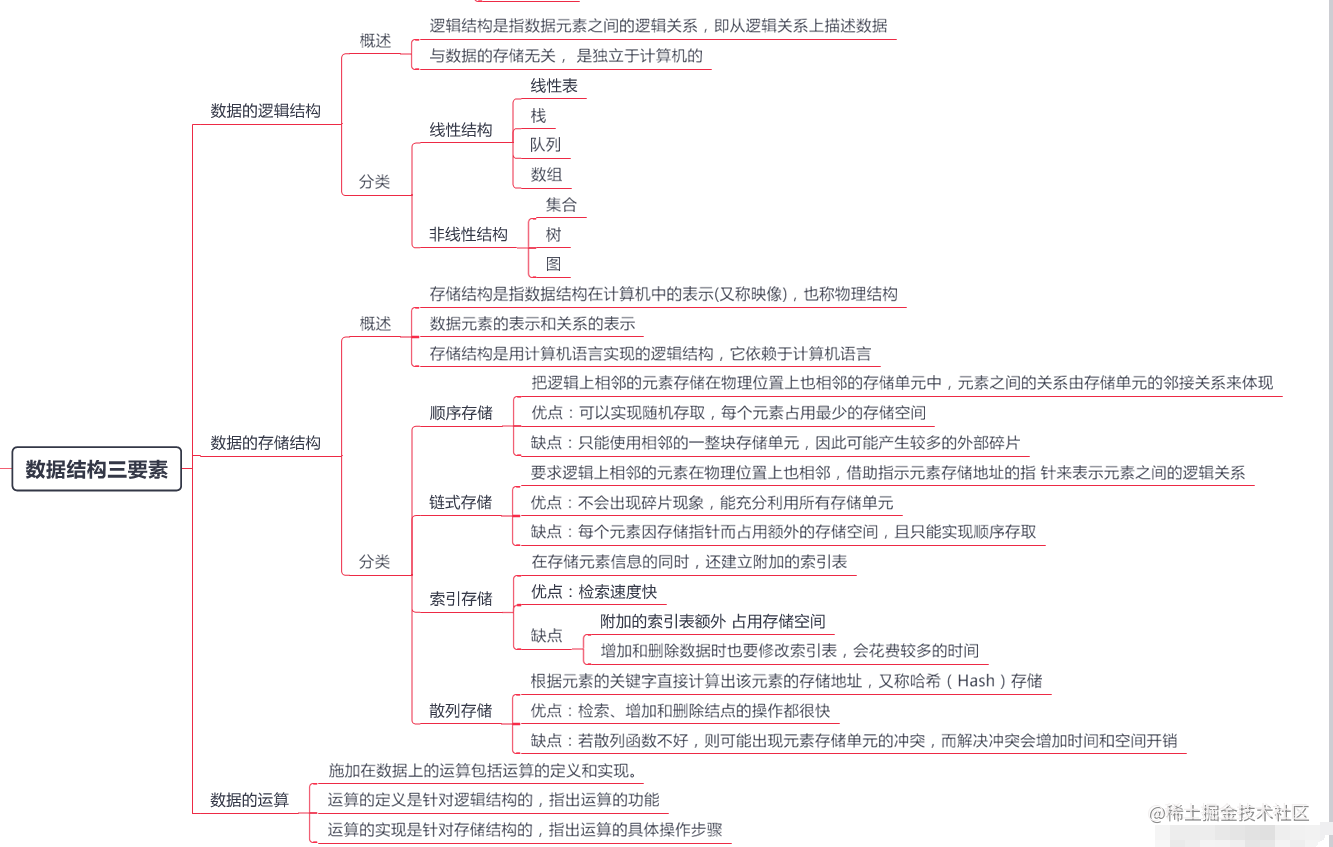
❗ 1.3.1 逻辑结构

逻辑结构:
\color{green}{逻辑结构:}
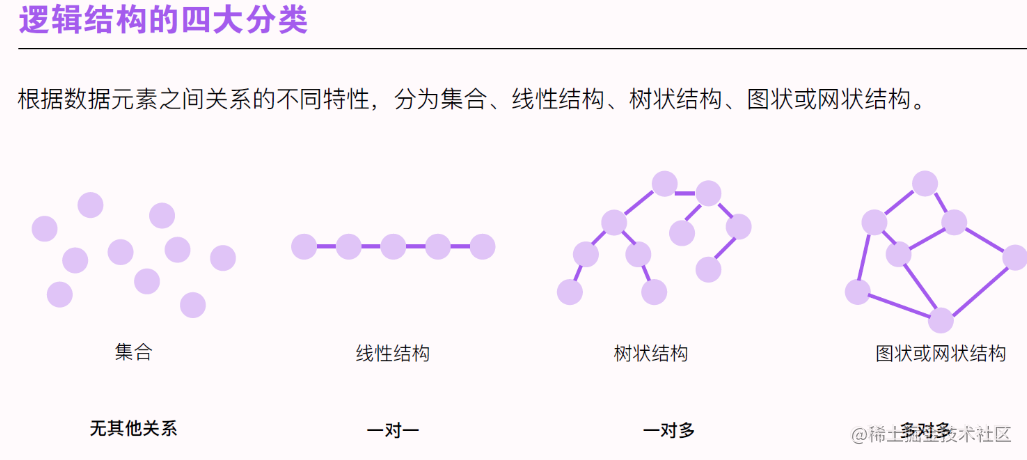
逻辑结构:是指数据元素之间的逻辑关系。
结构图:✨
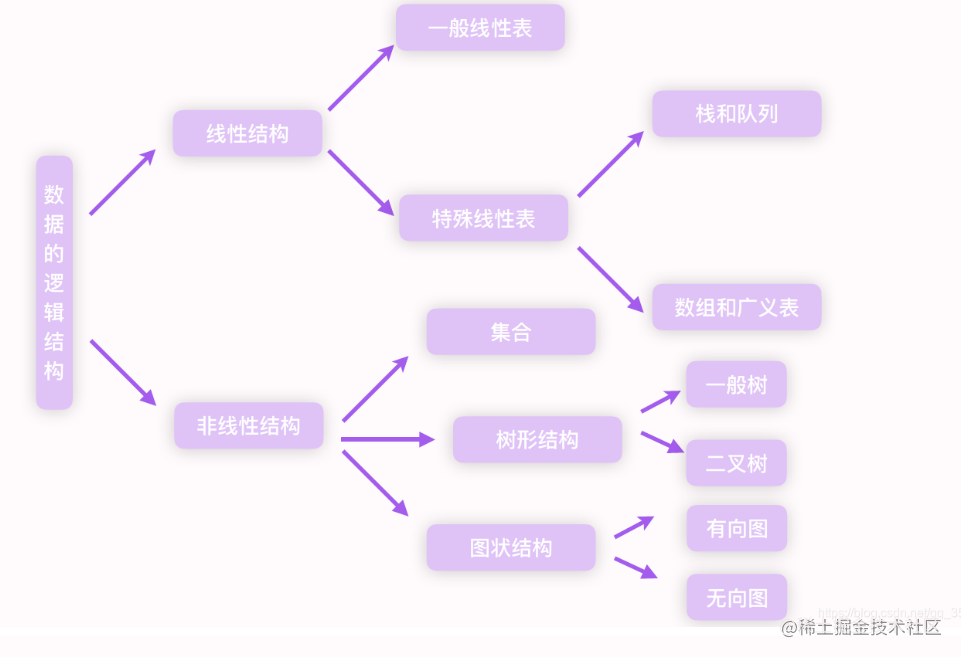
逻辑结构的四大分类:✨
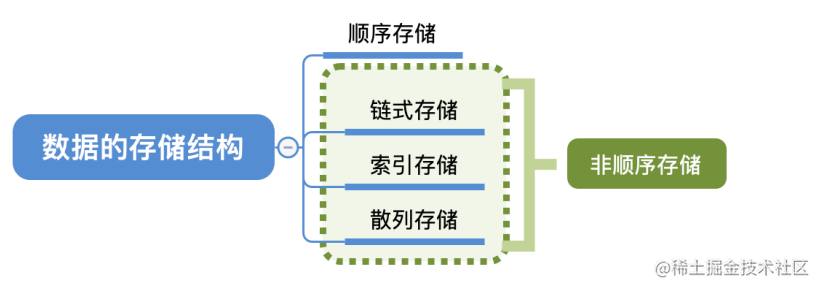
❗ 1.3.2 存储结构

逻辑结构 相当于“纸上谈兵”——是指“这个数据应该这样存,他们之间应该具有这样、那样的关系”,但是计算机可不管这么多,因为它就那么一个硬盘,还能玩出什么花样?
物理结构(存储结构) \color{blue}{物理结构(存储结构)} 物理结构(存储结构):是指数据的逻辑结构在计算机中的存储形式
数据的存储结构应该正确的反映数据元素之间的逻辑关系,这是实现物理结构的重点和难点。
主要分为: 顺序存储和链式存储 \color{#10c6f0}{顺序存储和链式存储} 顺序存储和链式存储
- 比如完全二叉树,它逻辑结构上很明显是树,但是在存储上可以用顺序存储(数组)也可以用链式存储(链表)
顺序存储结构 ( …数组)
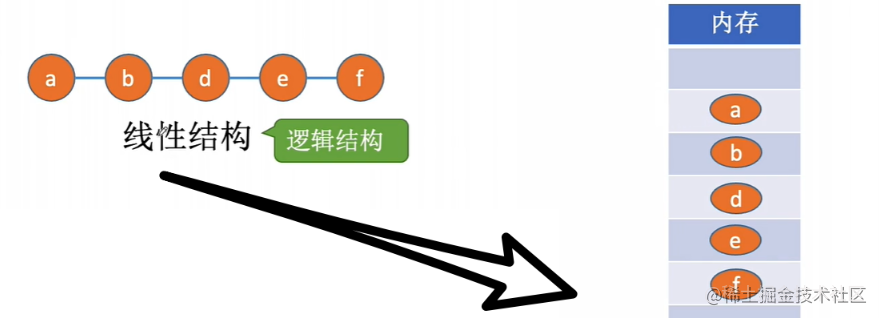
顺序存储结构 \color{#f82024}{顺序存储结构} 顺序存储结构:把 逻辑上相邻 \color{green}{逻辑上相邻} 逻辑上相邻的元素存储在 物理位置也相邻的存储单元 \color{blue}{物理位置也相邻的存储单元} 物理位置也相邻的存储单元中。元素之间的关系由存储单元的邻接关系体现
-
你可以这样理解,排队坐位置,规定好了A后面是B,那么B在坐的时候一定要坐到与A相邻的位置
-
最典型的就是数组
链式存储结构 (…链表)
链式存储结构
\color{#1d31fc}{链式存储结构}
链式存储结构:不要求
逻辑上相邻
\color{green}{逻辑上相邻}
逻辑上相邻的元素存储在
物理位置也相邻的存储单元
\color{orange}{物理位置也相邻的存储单元}
物理位置也相邻的存储单元中。元素之间的关系借助指示元素存储地址的指针来表示
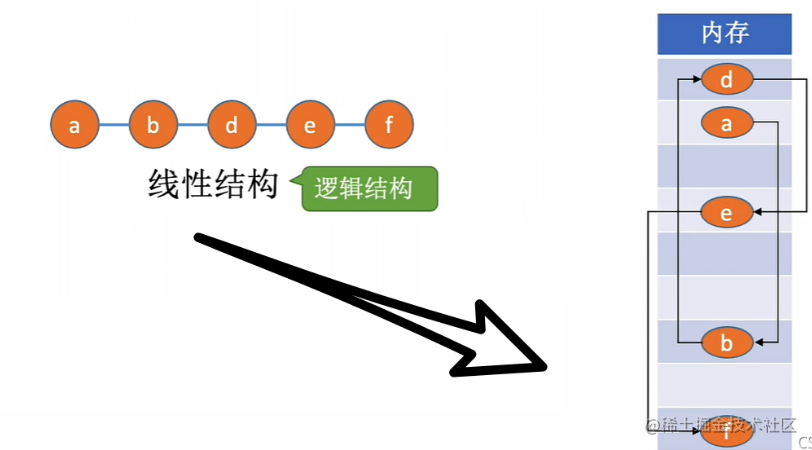
- 上例中这些元素逻辑上相邻,但所存放的存储单元并不是连续的(地址不一定连续)
索引存储结构
索引存储结构
\color{#1d31fc}{索引存储结构}
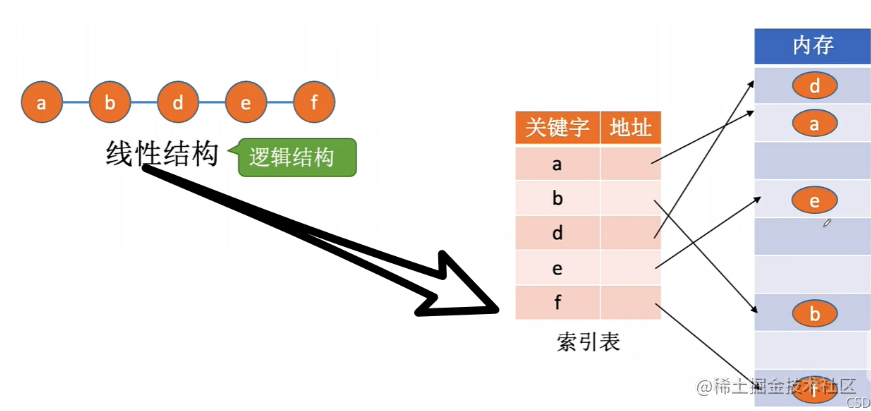
索引存储结构:在存储元素信息的同时,还建立附加的索引表。索引表中的每项称之为索引项,索引项一般形式是关键字+地址
散列存储结构
散列存储结构
\color{#1d31fc}{散列存储结构}
散列存储结构:根据元素的关键字
直接计算
\color{#1d31fc}{直接计算}
直接计算出该元素的地址。计算依靠的方式称之为哈希函数
详细介绍见后面的散列表
总结:
- 若采用
顺序存储,则各个数据元素在物理上必须是连续的;若采用非顺序存储,则各个数据元素在物理上可以是离散的。 - 数据的
存储结构会影响存储空间分配的方便程度 - 数据的
存储结构会影响对数据运算的速度
1.3.3 数据运算

数据运算 \color{orange}{数据运算} 数据运算:施加在数据上的元素包括运算的定义和实现
- 运算的
定义
\color{red}{定义}
定义是针对
逻辑结构的,指出运算的功能 - 运算的 实现 \color{green}{实现} 实现是针对 存储结构 \color{green}{存储结构} 存储结构的,指出运算的 具体步骤 \color{green}{具体步骤} 具体步骤
比如说:把信息插入线性表中
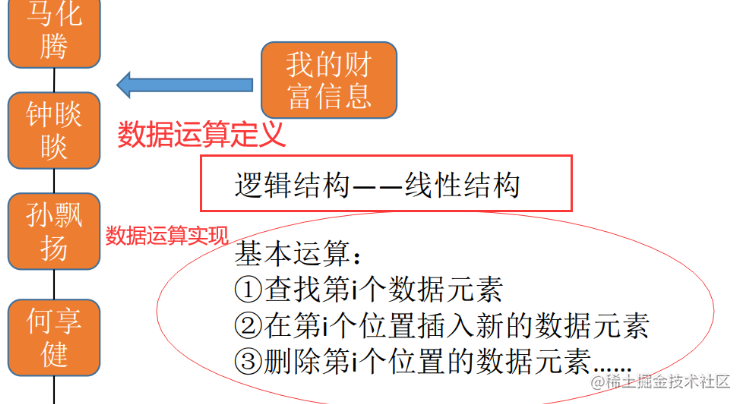
都是大佬啊

2. 时间空间复杂度(算法)

2.1 算法基本概念和评价
关于算法的基本概念和评价见:
算法的基本概念、算法的特性及设计要求
算法基本概念文件
❗❗ 2.2 时间空间复杂度✨
2.2.1❗❗时间复杂度✨✨
时间复杂度指算法中所有语句的频度(执行次数)之和。
主要根据问题规模n确定、公式是
T ( n ) = O ( f ( n ) ) T(n)=O(f(n)) T(n)=O(f(n))
比如下面这个过程!
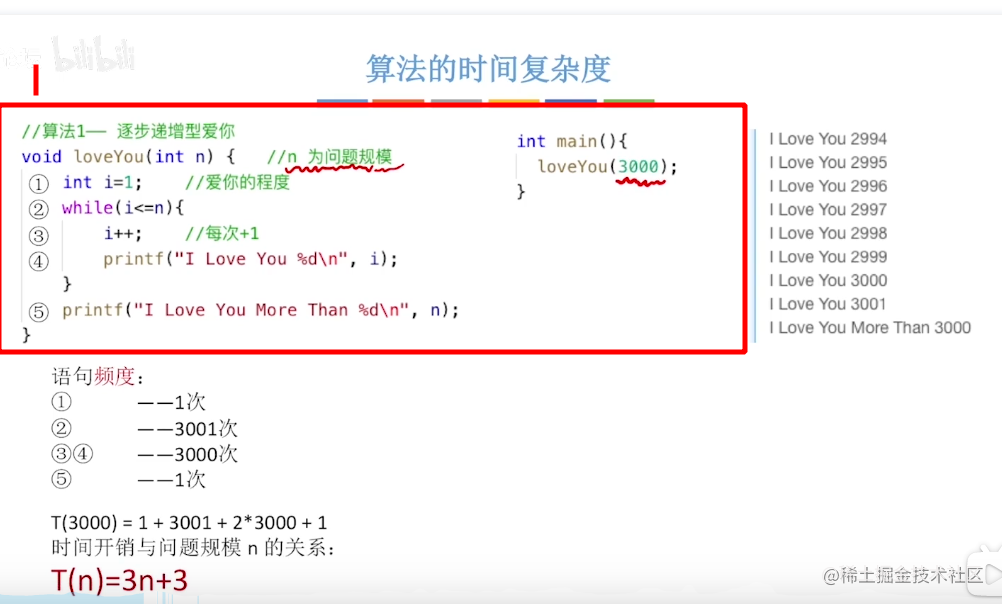
就是一个求出时间复杂度的过程,时间复杂度是T(n)=O(n);
方法就是取最大项
\color{green}{方法就是取最大项}
方法就是取最大项
推导出大O的方法:
B:推导大O阶的方法
推导基本方法如下
- 用常数1取代运行时间中的所有 加法常数 \color{blue}{加法常数} 加法常数·
- 在修改后的运行次数函数中,只保留 最高项数 \color{blue}{最高项数} 最高项数
- 如果最高项存在且不为1,则 去除与这个项相乘的常数 \color{blue}{去除与这个项相乘的常数} 去除与这个项相乘的常数
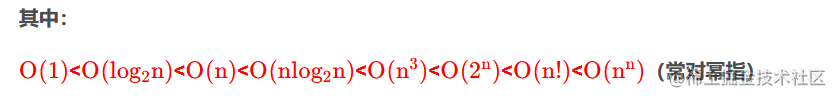
也可以用数学公式来解释:(利用除法求无穷极限)
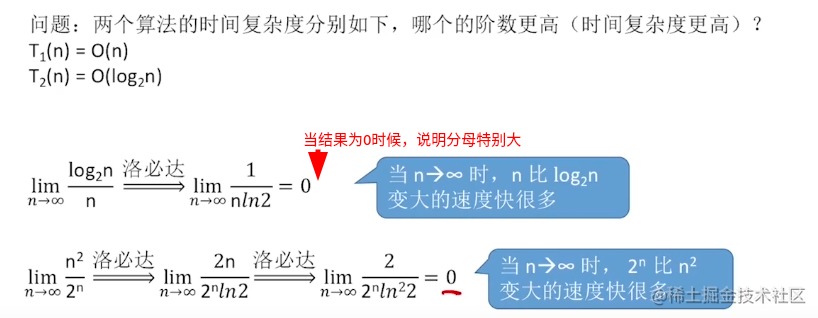
下面依次分析:
1. 常数阶 O(1)
高斯算法
//普通人
int i,sum=0,n=100; //执行1次
for(i=1;i<=n;i++)//执行n+1次
{
sum=sum+i;//执行n次
}
cout << sum;//执行1次
//大神高斯
int sum=0,n=100;//执行1次
sum=(1+n)*n/2;//执行1次
cout << sum//执行1次
高斯算法,很明显复杂度为O(1)
但是如果这样:
int sum=0,n=100;//执行1次
sum=(1+n)*n/2;//执行1次
sum=(1+n)*n/2;//执行2次
sum=(1+n)*n/2;//执行3次
sum=(1+n)*n/2;//执行4次
sum=(1+n)*n/2;//执行5次
sum=(1+n)*n/2;//执行6次
sum=(1+n)*n/2;//执行7次
sum=(1+n)*n/2;//执行8次
sum=(1+n)*n/2;//执行9次
sum=(1+n)*n/2;//执行10次
cout << sum//执行1次
初学者很容易被其中置入的这些代码误导
事实上,无论 n 为多少 ; 两段代码就是 3 和 12 的区别,仍然属于常数阶 \color{red}{事实上,无论n为多少;两段代码就是3和12的区别,仍然属于常数阶} 事实上,无论n为多少;两段代码就是3和12的区别,仍然属于常数阶 , 也就是 O ( 1 ) 同时对于分支结构,无论是真是假,执行的次数都是恒定的 \color{red}{也就是O(1)同时对于分支结构,无论是真是假,执行的次数都是恒定的} 也就是O(1)同时对于分支结构,无论是真是假,执行的次数都是恒定的 , 所以单纯的分支结构〈不包含在循环中 ) ,其时间复杂度也是 O ( 1 ) \color{red}{所以单纯的分支结构〈不包含在循环中),其时间复杂度也是O(1)} 所以单纯的分支结构〈不包含在循环中),其时间复杂度也是O(1)
2.线性阶
如下代码由于循环体中的代码执行n次,因此其时间复杂度为O(n)
int i
for(i=0;i<n;i++)
{
//时间复杂度为O(1)的程序步骤序列
}
就是在循环中,看循环多少
3.对数阶
如下代码,由于循环中count乘以2之后,距离循环结束条件的n就更近了一步
int count = 1;
while(count < n)
{
count = count*2;
//时间复杂度O(1)的程序步骤序列
......
}
也就是说现在在问你:
有多少个count*2后会大于n,那么自然得到答案是
l
o
g
2
n
log_2{n}
log2n,所以时间复杂度是O(
l
o
g
2
n
log_2{n}
log2n)
过程如下:
4. 平方阶
如下例子,存在两个for循环,很明显其时间复杂度为O(mn),且当m=n时,时间复杂度为O(n^2),所以, 循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。 \color{red}{循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。} 循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
int i,j;
for(i =0;i<m;i++)
{
for(j=0;j<n;j++)
{
//时间复杂度为O(1)的程序步骤序列
}
}
等于循环嵌套时候要注意下!
下面的这个例子呢? 当i=1的时候执行n次,当n=2的时候执行(n-1)次,…
明显这是一个等差数列,n+(n-1)+(n-2)+…+1
求和易得:n+n*(n-1)/2
整理一下就是n*(n+1)/2
然后我们将其展开可以得到n^2/2+n/2。
根据我们的步骤走,保留最高次项,去掉相乘的常数就可以得到时间复杂度为:O(n^2)
public class TS {
public static void main(String[] args) {
int sum = 0;
for(int i=1;i<=100;i++) {
for(int j=i;j<=100;j++)
sum = sum + i;
}
}
}
递归时候情况
另外还有一种情况较为常见,那就是对于 递归, \color{red}{递归,} 递归,递归算法其时间复杂度为: 递归次数 ∗ 每次递归的次数。 \color{red}{递归次数*每次递归的次数。} 递归次数∗每次递归的次数。
下面例子时间复杂度为O(n)
// 计算阶乘递归Factorial的时间复杂度?
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}
就是自己调用自己,这里按照公式来写:
每次 n − 1 \color{RED}{n-1} n−1,递归了n次时间复杂度是 o ( n ) \color{RED}{o(n)} o(n),每次进行了一个乘法操作,乘法操作的时间复杂度一个常数项 o ( 1 ) \color{RED}{o(1)} o(1),所以这份代码的时间复杂度是 O ( n ) × O ( 1 ) = O ( n ) 。 \color{RED}{O(n)× O(1) = O(n)。} O(n)×O(1)=O(n)。
如果感兴趣的话可以读读这篇文章比较深入:# 递归算法的时间复杂度(面试)
5.线性对数阶O(nlogN)
for (int m = 1; m <= n; m++) {
int i = 1;
while (i < n)
i = i * 2;
}
下面那段就是对数阶O(logn)的代码,上面加了个for循环了n次,它的时间复杂度就是 n * O(logn),也就是了O(nlogn),归并排序的复杂度就是O(nlogn)。
2.2.2 ❗❗最坏\最好\平均时间复杂度✨✨
大家会发现代码过程(例如查找)中有这样几种情形:
- 最好时间复杂度:第—次就找到了,时间复杂度为O(1)
- 最坏时间复杂度,第n次才能找到,时间复杂度为O(n)
for (int i=0; i < n; ++i) {
if (girlArray[i] == number) {
pos = i;
break;
}
其实最好与最坏都是极端情况,发生的概率并不大。为了能更好的的表示平均情况下的时间复杂度,在这里引入了一个新的词汇 ∗ 平均情况时间复杂度 ∗ \color{red}{*平均情况时间复杂度*} ∗平均情况时间复杂度∗
分析:
变量 number 在 girlArray 数组中出现的情况有 n + 1 种,在数组中 n 种,不在数组中 1 种。
每种情况我们要遍历的次数都不一样,我们把每种情况需要遍历的次数累加,然后再除以所有情况数 n + 1,就能得到需要遍历次数的平均值。
公式就是: ∗ 平均情况时间复杂度 = 每种情况遍历次数累加和 / 所有情况数量 ∗ \color{red}{*平均情况时间复杂度 = 每种情况遍历次数累加和 / 所有情况数量*} ∗平均情况时间复杂度=每种情况遍历次数累加和/所有情况数量∗
平均情况时间复杂度为:
((1+2+3+…+n-1) + n) / (n + 1) = n*(n+1)/2(n+1)
O(n)
而我们在 描述算法的复杂度给出的是最坏情况 \color{orange}{描述算法的复杂度给出的是最坏情况} 描述算法的复杂度给出的是最坏情况,因为这已经是最坏的了,那么剩余的情况肯定就这个好
所以时间空间复杂度其实考虑的是最差的情况
2.2.3 ✨ 空间复杂度
算法的空间复杂度定义为: s ( n ) = o ( g ( n ) ) \color{green}{s (n) =o (g (n) )} s(n)=o(g(n))
表示随着问题规模n的增大,算法运行所需存储量的增长率与g (n)的增长率相同。
其中,n为问题的规模,g(n)为语句关于n所占存储空间的函数
算法的存储量包括 \color{purple}{算法的存储量包括} 算法的存储量包括
- 输入数据所占空间。
- 程序本身所占空间。
- 辅助变量所占空间。
若算法执行时所需要的辅助空间相对于输入数据量而言是一个常数,则称此算法为原地工作,其空间复杂度为O(1)
若所需存储量依赖于特定的输入,则通常按最坏情况考虑。
变量—O(1)
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
共定义了 *a n end end i 五个变量,去除常数 还是O(1)
数组—O(n)
#O(n)
list1 = 'physics', 'chemistry , 1997,2000
申请了一个数组,O(N)
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long * fibArray =
(long long *)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
波那契数列开辟了N+1个空间,故空间复杂度为O(N)
二维数组 0(n^2)
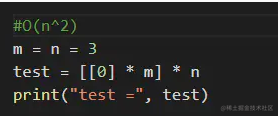
递归
// 计算阶乘递归Factorial的空间复杂度?
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N - 1)*N;
}
递归调用了n次,Factorial(N - 1)*N;
每次开辟一个空间给下一个Factorial用,
开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝🌝
祝大家学习快乐,总结…
参考:
- 一套图搞懂时间复杂度
- 算法的时间复杂度和空间复杂度
- 看懂时间复杂度
- # 时间复杂度和空间复杂度的计算
- 计算时间复杂度简单版
- 算法初认识
- # 最好、最坏、平均时间复杂度
- # (王道408考研数据结构)第一章绪论-第二节2:算法的时间复杂度和空间复杂度











![[附源码]计算机毕业设计Python的中点游戏分享网站(程序+源码+LW文档)](https://img-blog.csdnimg.cn/b921b88959d141e78633b79cbeaa2ea0.png)