目录

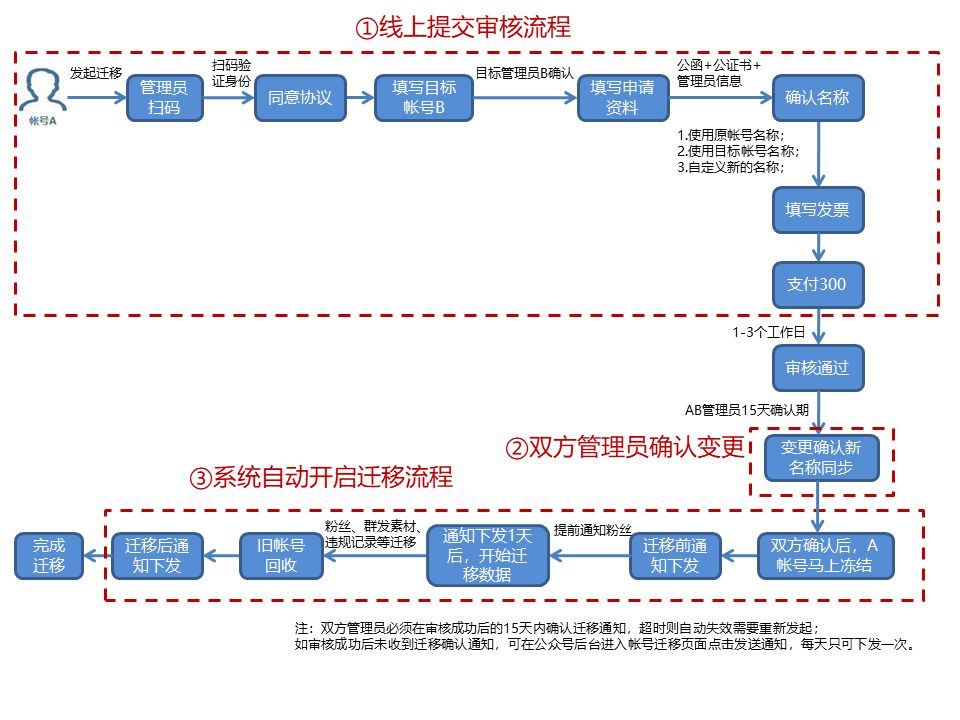
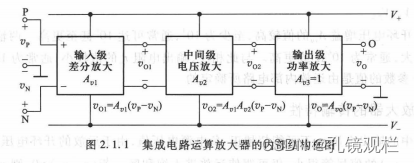
 1、结构组成：差分放大电路、电压放大电路、功率放大电路。

 2、同相放大器：

 3、反相放大器：一个正电压放大并变为负电压。

 4、差分放大电路：输入两个不同的电压，两者的差值乘以放大系数得到输  出电压。

 1、结构组成：差分放大电路、电压放大电路、功率放大电路。

差分放大电路：其对称性可提高整个电路的性能。

电压放大电路：在于提高电压的增益。

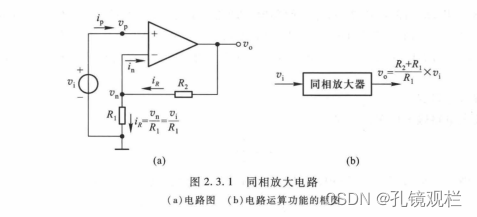
 2、同相放大器：

使用Multisim软件验证如下：

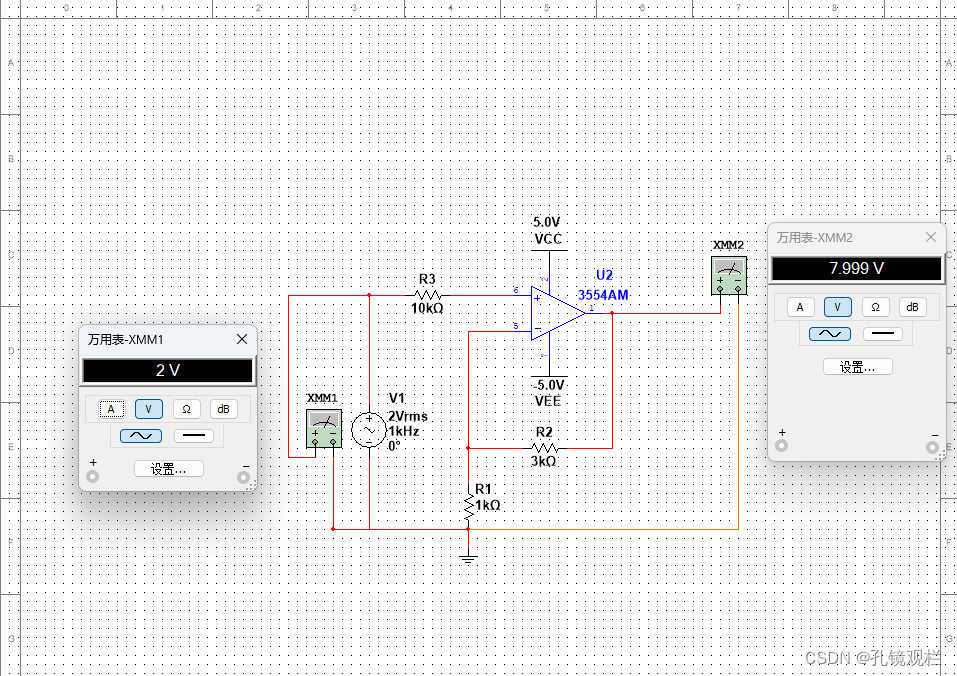
 计算公式：

Vo=(1+R2/R1)*Vi

V0=(1+3/1)*2v=8v 与仿真的结果基本一致。

 3、反相放大器：一个正电压放大并变为负电压。

计算公式：

Vout=-(R2/R3)*Vin

Vout=-(3/1)*2V=-6V

万用表看不出反相的结果,用示波器比较明显，输入电压2v时，输出电压为-6v。

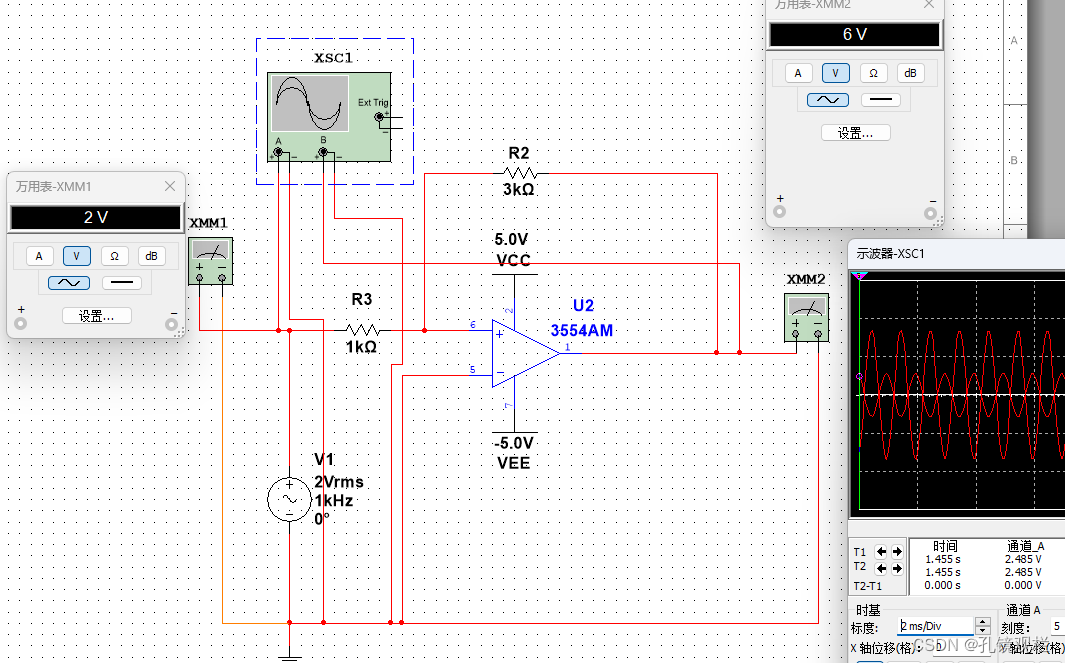
4、差分放大电路：输入两个不同的电压，两者的差值乘以放大系数得到输出电压。

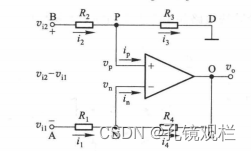
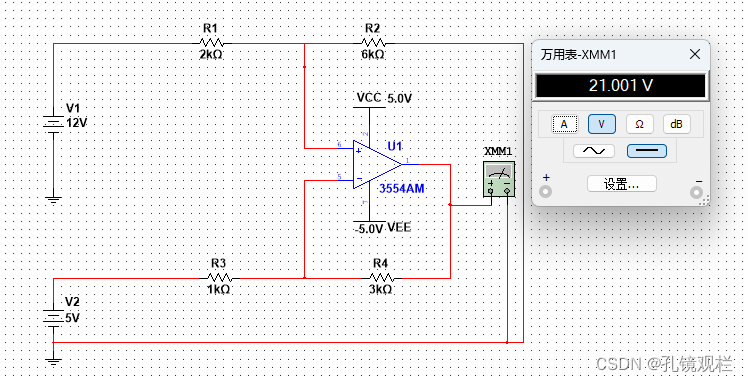
输出电压公式为Vo=R4/R1(Vi1-Vi2),Av=R4/R3=R2/R1，Av为差模电压增益。

即Vo=(3k/1k)*(12-5)V=3*7v=21v，理论计算结果与仿真效果几乎一致。