目录
第一题
题目来源
题目内容
解决方法
方法一:暴力枚举
方法二:哈希表
第二题
题目来源
题目内容
解决方法
方法一:动态规划
第三题
题目来源
题目内容
解决方法
方法一:模拟
第一题
题目来源
两数之和 - 力扣(LeetCode)
题目内容

解决方法
方法一:暴力枚举
class Solution {
public int[] twoSum(int[] nums, int target) {
// 遍历每个数字
for (int i = 0; i < nums.length; i++) {
// 从当前数字的下一个位置开始遍历
for (int j = i + 1; j < nums.length; j++) {
// 判断两个数字之和是否等于目标值
if (nums[i] + nums[j] == target) {
// 如果满足条件,则返回两个数字的下标
return new int[] {i, j};
}
}
}
// 若没有找到满足条件的组合,则抛出异常
throw new IllegalArgumentException("No two sum solution");
}
}这段代码使用了两个嵌套的循环来遍历数组。外层循环从第一个元素开始,内层循环从外层循环的下一个位置开始。在内层循环中,判断当前两个数字的和是否等于目标值。如果满足条件,就返回这两个数字的下标。如果整个数组都遍历完后没有找到满足条件的组合,就抛出异常表示没有解。
该算法的时间复杂度为 O(n^2),因为需要遍历每对不同的数字。空间复杂度为 O(1),因为没有使用额外的空间来存储数据。
LeetCode运行结果:
方法二:哈希表
注意到方法一的时间复杂度较高的原因是寻找 target - x 的时间复杂度过高。因此,我们需要一种更优秀的方法,能够快速寻找数组中是否存在目标元素。如果存在,我们需要找出它的索引。
import java.util.HashMap;
import java.util.Map;
class Solution {
public int[] twoSum(int[] nums, int target) {
// 创建一个哈希表,用于存储数组中每个数字对应的索引
Map<Integer, Integer> map = new HashMap<>();
// 遍历数组
for (int i = 0; i < nums.length; i++) {
// 计算当前数字与目标值的差值
int complement = target - nums[i];
// 检查差值是否已经在哈希表中存在
if (map.containsKey(complement)) {
// 如果存在,则返回差值的索引和当前数字的索引
return new int[] {map.get(complement), i};
}
// 将当前数字添加到哈希表中,索引作为值,数字作为键
map.put(nums[i], i);
}
// 若没有找到满足条件的组合,则抛出异常
throw new IllegalArgumentException("No two sum solution");
}
}这段代码使用了哈希表来优化查找过程。遍历数组时,我们计算当前数字与目标值的差值,并检查该差值是否已经在哈希表中存在。如果存在,则说明之前遍历过的某个数字与当前数字的和等于目标值,就返回这两个数字的索引。如果不存在,则将当前数字添加到哈希表中,以便后面的数字可以使用它作为差值进行查找。
该算法只需要一次遍历数组,时间复杂度为 O(n)。同时,通过使用哈希表来存储数字和索引的映射关系,可以在 O(1) 的时间复杂度内快速查找差值是否已存在。
LeetCode运行结果:
第二题
题目来源
打家劫舍 - 力扣(LeetCode)
题目内容

解决方法
方法一:动态规划
题目描述已经很清楚了。这是一个动态规划问题。
解题思路:
1、假设dp[i]表示到第i个房间时能够获得的最大金额。
2、状态转移方程:dp[i] = max(dp[i-2]+nums[i], dp[i-1]),表示选择偷当前房间和前两个房间的收益之和与不偷当前房间的收益中的较大值。
3、最终结果为dp[nums.length-1]。
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int n = nums.length;
if (n == 1) {
return nums[0];
}
int[] dp = new int[n]; // 创建一个长度为n的数组,存储中间结果
dp[0] = nums[0]; // 第一个房间的最大金额就是它本身的金额
dp[1] = Math.max(nums[0], nums[1]); // 第二个房间的最大金额是第一个房间和第二个房间之间金额较大的那个
for (int i = 2; i < n; i++) {
// 当前房间的最大金额是选择偷当前房间和前两个房间的收益之和与不偷当前房间的收益中的较大值
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[n - 1]; // 返回最后一个房间的最大金额
}
}
时间复杂度分析: 遍历数组一次,时间复杂度为O(n)。其中n为数组的长度。
空间复杂度分析: 需要一个长度为n的数组来存储中间结果,因此空间复杂度为O(n)。其中n为数组的长度。
LeetCode运行结果:
第三题
题目来源
2. 两数相加 - 力扣(LeetCode)
题目内容
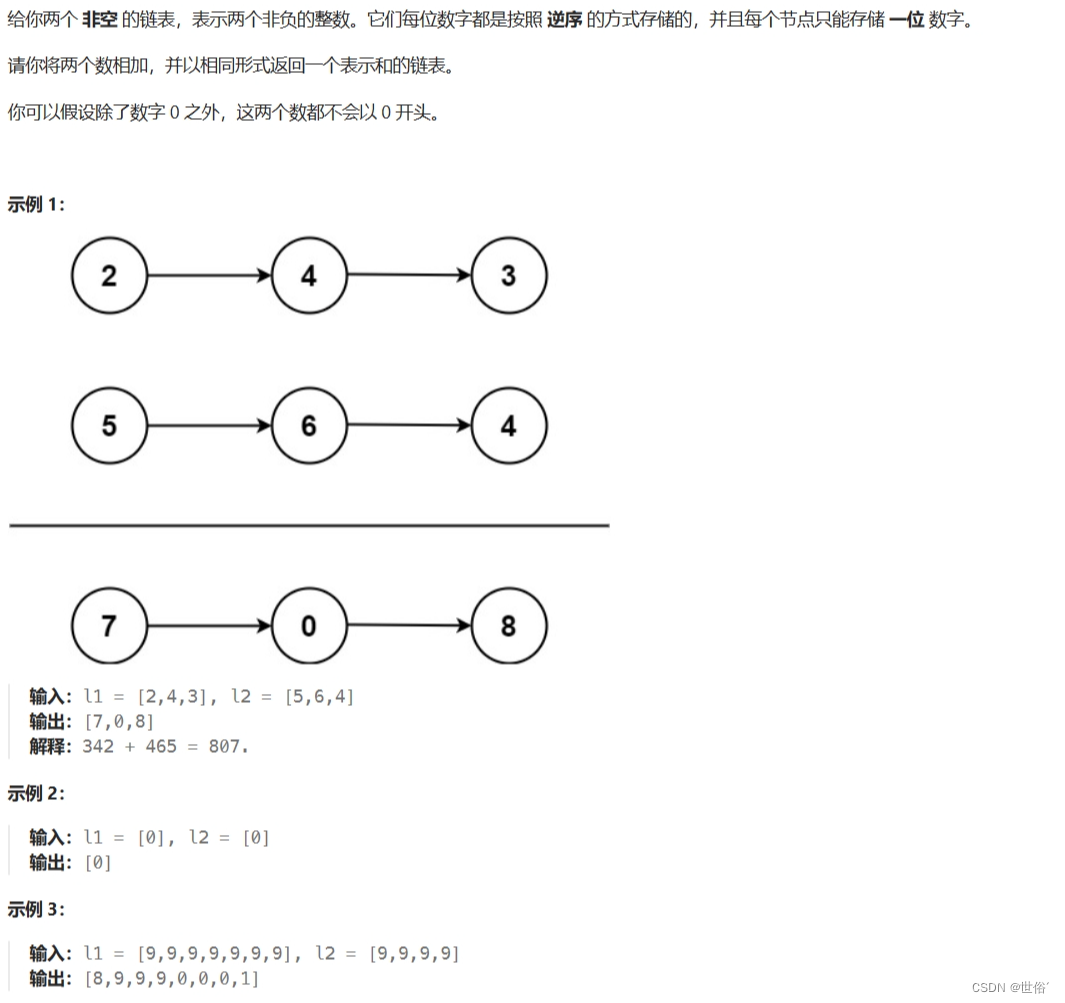

解决方法
方法一:模拟
分析思路与算法如下:
需要实现了两个链表的逐位相加,并返回一个新的链表表示其和。算法的主要思路是使用两个指针分别指向两个链表的当前节点,同时使用一个进位变量来记录上一位的进位情况。
具体算法步骤如下:
- 创建一个哑节点作为结果链表的头节点,并创建一个指针curr指向哑节点。
- 初始化进位变量carry为0。
- 使用一个循环遍历两个链表,直到两个链表都遍历完毕。
- 在每一次循环中,首先获取当前节点的值,并将两个节点的值以及进位相加,得到一个新的和。
- 将新的和对10取余数,即为当前位的值,并创建一个新的节点插入到结果链表中。
- 更新进位变量,将和除以10并取整,得到新的进位值。
- 将指针curr后移一位,指向刚插入的新节点。
- 如果其中一个链表已经遍历完了,但另一个链表还有剩余节点,那么继续处理剩余节点,并将进位值考虑在内。
- 最后检查进位变量是否为0,如果不为0,则追加一个新节点表示最高位的进位。
- 返回结果链表的头节点(去掉哑节点)。
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0); // 创建哑节点
ListNode curr = dummy; // 当前指针指向哑节点
int carry = 0; // 进位变量
while (l1 != null || l2 != null) {
int val1 = l1 != null ? l1.val : 0;
int val2 = l2 != null ? l2.val : 0;
int sum = val1 + val2 + carry; // 计算当前位的和
carry = sum / 10; // 更新进位值
curr.next = new ListNode(sum % 10); // 创建新节点并插入结果链表
curr = curr.next; // 指针后移一位
if (l1 != null) l1 = l1.next;
if (l2 != null) l2 = l2.next;
}
if (carry != 0) {
curr.next = new ListNode(carry); // 还有一个进位没有算进去,追加一个新节点
}
return dummy.next; // 返回结果链表的头节点(去掉哑节点)
}
}
复杂度分析如下:
- 时间复杂度:假设两个链表的长度分别为 m 和 n,我们需要遍历两个链表中的所有节点,时间复杂度为 O(max(m, n))。
- 空间复杂度:除了存储结果链表以外,我们只使用了常数级别的额外空间,因此空间复杂度为 O(1)。
综合来看,该代码在时间和空间上都具有较优的复杂度。
LeetCode运行结果: