首先，我们要引入一个一道题目1. 两数之和 - 力扣（LeetCode）

两数之和

其实这道题很简单，但是，可以使用内嵌循环来进行遍历，找到符合要求的数据，返回下标即可。

但今天提供另一个方法，可以大大的简化时间复杂度

——双指针

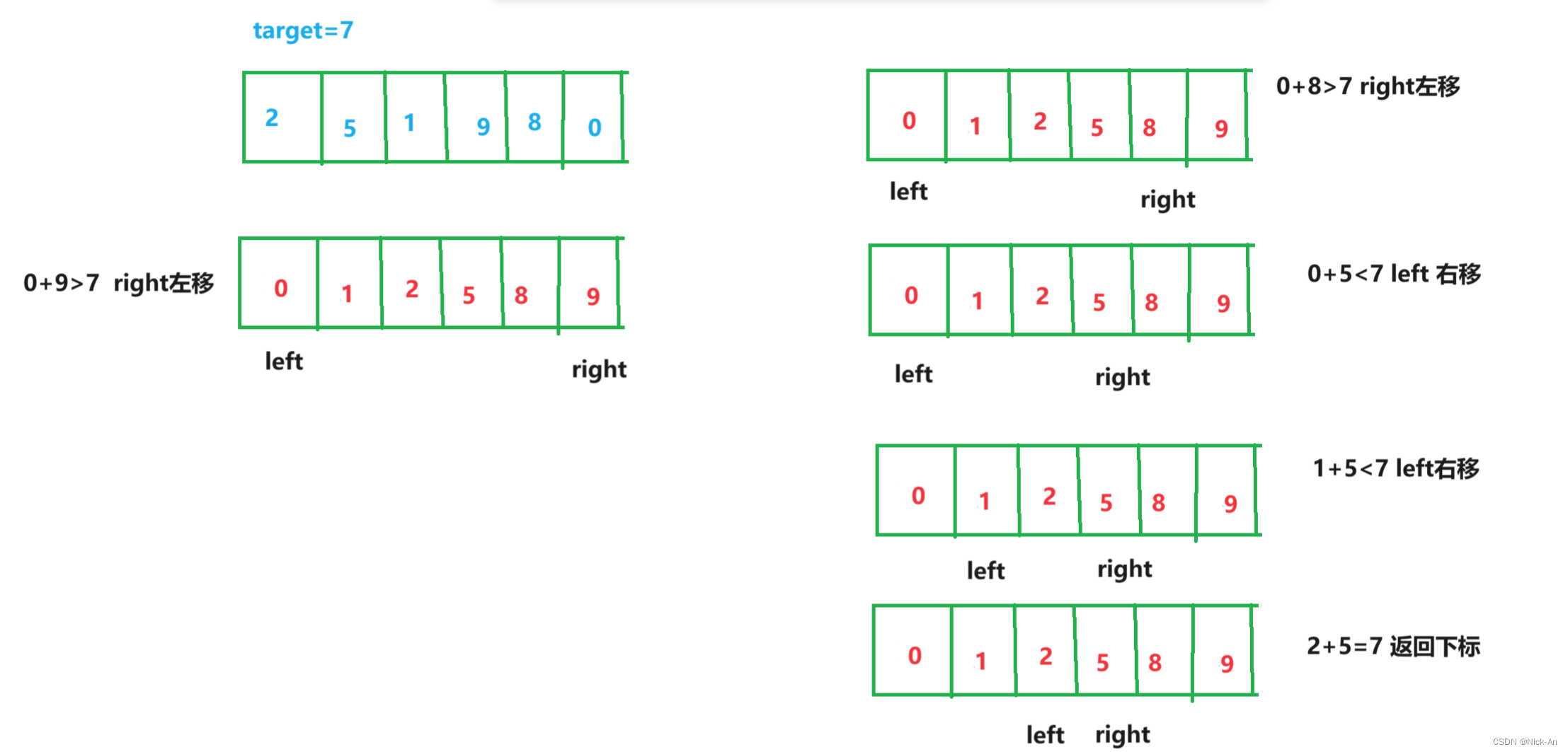
1.先将数据进行一个排序，从两头向中间遍历

2.左右数据的和，若大于target，那么左指针右移，若小于target，那么右指针左移，若为target，那么就返回left和right，恰好对应着两个数据的下标。

以此题为例

弊端

因为返回的是数组下标，所以在排序后，原来的数据对应的下标就会被改变，除非是已经升序排序的数组，或者是返回是数组的数据内容。

以此有一个拓展——

三数求和

15. 三数之和 - 力扣（LeetCode）

这道题，我们也可以通过这个思想来做

注意

此题最重要的就是数据的去重，不仅仅是一开始就定好的i，对于left和right，在进行sum求和后

left对于右移后的数据left+1，那么两个数据不能相同，若相同，则需要跳过

right对于左移后的数据right-1，那么两个数据不能相同，若相同，则需要跳过

代码如下

 vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end()); // 对数组进行排序，以便后续操作
        vector<vector<int>> answer; // 存储结果的二维向量
        
        for (int i = 0; i < n - 2; i++) { // 遍历数组，固定第一个元素
            // 避免重复的固定元素
            if (i > 0 && nums[i] == nums[i - 1])
            //因为是从相邻两个开始相加的，所以若两个相同，那么此次循环跳过
            //到下一个新的循环里
                continue;

            int left = i + 1; // 左指针指向固定元素的下一位
            int right = n - 1; // 右指针指向数组末尾
            
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right]; // 计算三个元素的和

                if (sum < 0) { // 如果和小于零，说明需要增大和，左指针右移一位
                    left++;
                }
                else if (sum > 0) { // 如果和大于零，说明需要减小和，右指针左移一位
                    right--;
                }
                else { // 和等于零，找到满足条件的三元组
                    answer.push_back({nums[i], nums[left], nums[right]}); // 将三元组添加到结果中
                    
                    // 避免重复的左指针元素——重复的元素就跳过  -1 -1 0 1 1  这样子就只有一组
                    while (left < right && nums[left] == nums[left + 1])
                        left++;
                    // 避免重复的右指针元素
                    while (left < right && nums[right] == nums[right - 1])
                        right--;
                    
                    //修正后再次移动
                    left++; // 左指针右移一位
                    right--; // 右指针左移一位
                }
            }
        }  
        return answer;
    }