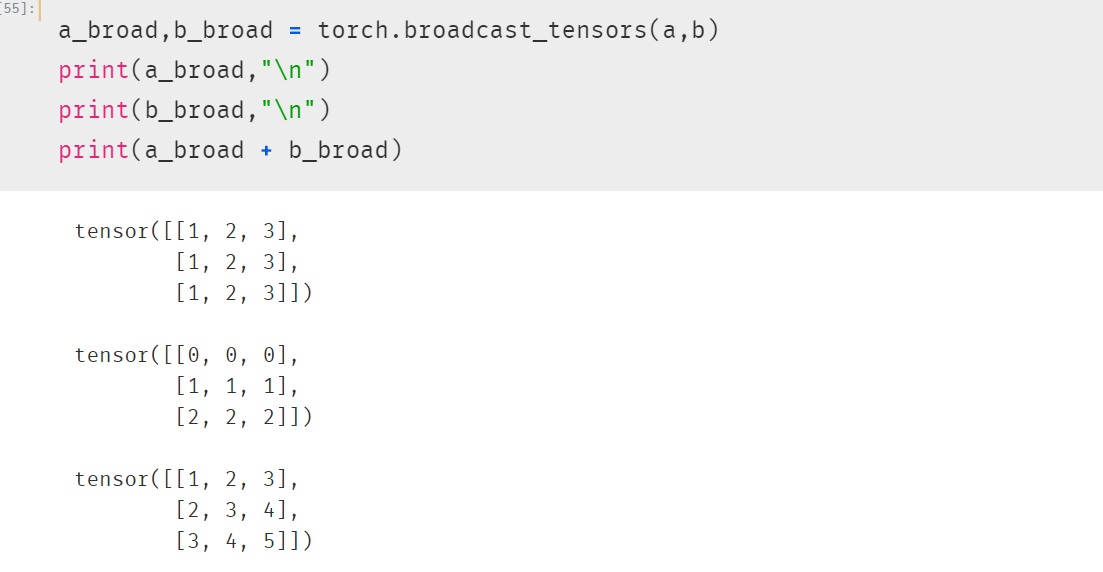
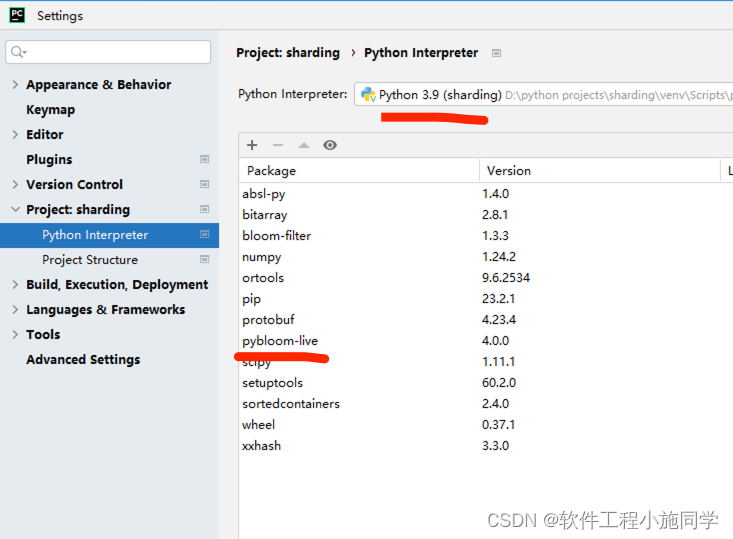
1. 安装pybloom_live

from pybloom_live import BloomFilter

# 创建一个Bloom过滤器对象
# 错误率（False Positive Rate）在布隆过滤器中指的是，不存在的元素被错误地认为存在于集合中的概率
bf = BloomFilter(capacity=10000, error_rate=0.001)

# 添加元素到Bloom过滤器中
bf.add("apple")
bf.add("banana")
bf.add("orange")

# 判断元素是否在集合中
print(bf.__contains__("apple"))  # True
print(bf.__contains__("grape"))  # False

print(bf.__getstate__())  # 查看布隆过滤器状态

# 打开文件，如果文件不存在则创建
with open('output.txt', 'wb+') as f:
    # 将Bloom过滤器写入文件
    bf.tofile(f)

# print(len(bf.bitarray))

# 打开文件，如果文件不存在则创建
with open('output.txt', 'rb+') as f2:
    # 从文件中恢复Bloom过滤器
    bf2 = BloomFilter.fromfile(f2)
    print(bf2.__getstate__())  # True
    print(bf2.__contains__("apple"))  # True
    print(bf2.__contains__("grape"))  # False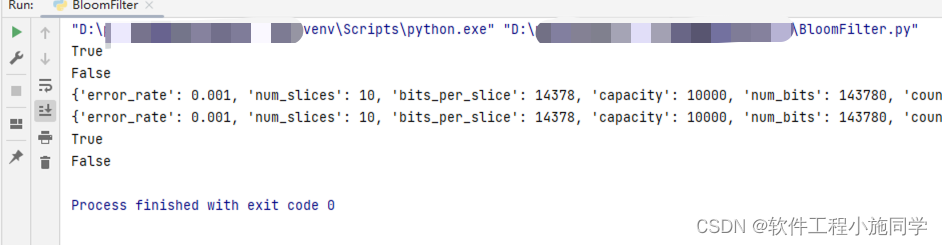

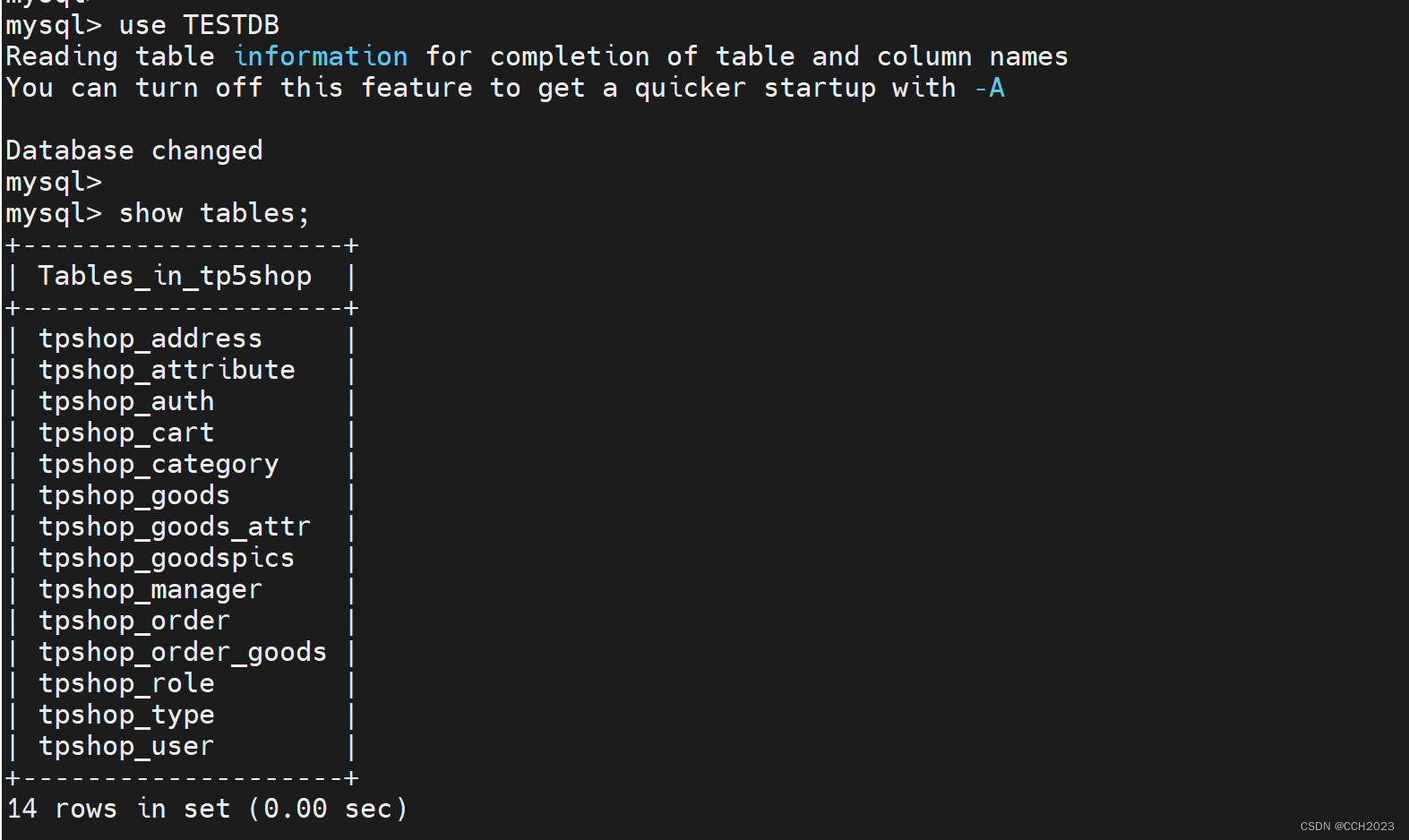
它有很多函数

假设错误率设置为0.001，bf.add了3个元素

如果是容量设置为10000个，存储开销是18kb

设置是容量设置为10万个，存储开销是176kb

设置是容量设置为10万个，假设bf.add了10000个元素

176kb

开销不变

如果是把这10000个元素直接存到txt中

38k

布隆过滤器是一种空间效率极高的概率型数据结构，它利用位数组和哈希函数来判断一个元素是否在一个集合中。它的时间复杂度和空间复杂度如下：

时间复杂度：对于判断一个元素是否在一个集合中，布隆过滤器的时间复杂度为O(k)，其中k为哈希函数的数量。因为我们需要将元素通过k个哈希函数映射到位数组中的k个位置，并检查这些位置是否为1。

空间复杂度：布隆过滤器的空间复杂度取决于位数组的大小。假设位数组的大小为m，那么空间复杂度为O(m)。

需要注意的是，布隆过滤器可能会产生假阳性（False Positive），即可能会将一个不在集合中的元素误判为在集合中。但不会产生假阴性（False Negative），即如果判断一个元素不在集合中，那么这个元素肯定不在集合中。

软件工程小施同学

20230914