张量数学运算主要有：标量运算，向量运算，矩阵运算，以及使用非常强大而灵活的爱因斯坦求和函数torch.einsum（重难点）进行任意维的张量运算。此外还会介绍张量运算的广播机制。

一，标量运算 (操作的张量至少是0维)

张量的数学运算符可以分为标量运算符、向量运算符、以及矩阵运算符。
加减乘除乘方，以及三角函数，指数，对数等常见函数，逻辑比较运算符等都是标量运算符。
标量运算符的特点是对张量实施逐元素运算。
有些标量运算符对常用的数学运算符进行了重载。并且支持类似numpy的广播特性。
以下记录一些重难点：

1. torch.max和torch.min

2. torch.round floor ceil trunc

3. torch.fmod remainder

4. 幅值裁剪 torch.clamp

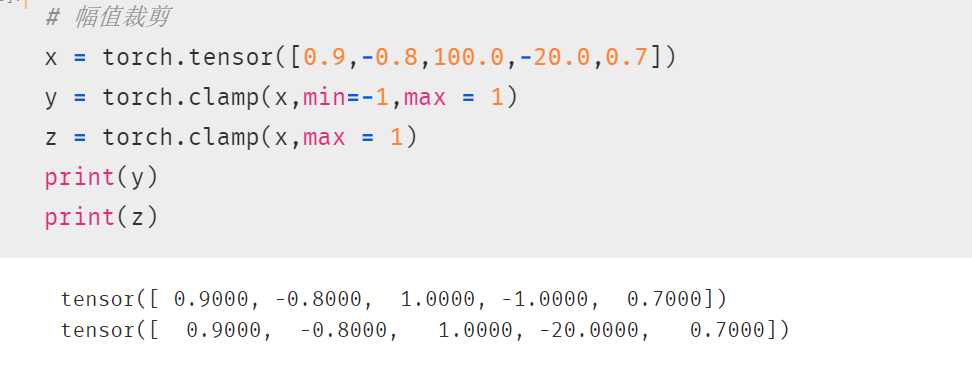
二、向量运算

1. cum扫描

torch.cumsum：返回维度dim中输入元素的累计和。例如，如果输入是大小为N的向量，则结果也将是大小为N的带有元素的向量。【运算后维度不变】
这里统一解释以下维度：
如果是一维数据（一维向量）：

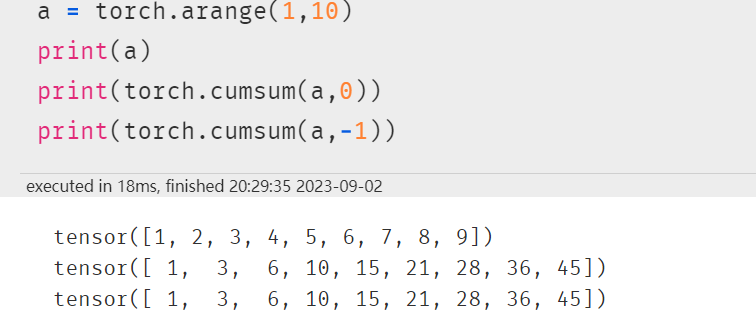
一维数据的规模结果就只有一个数，这里算出来就是6，dim=0，指的是列不变，dim=-1也是指的列不变。
如果是二维数据（矩阵）：

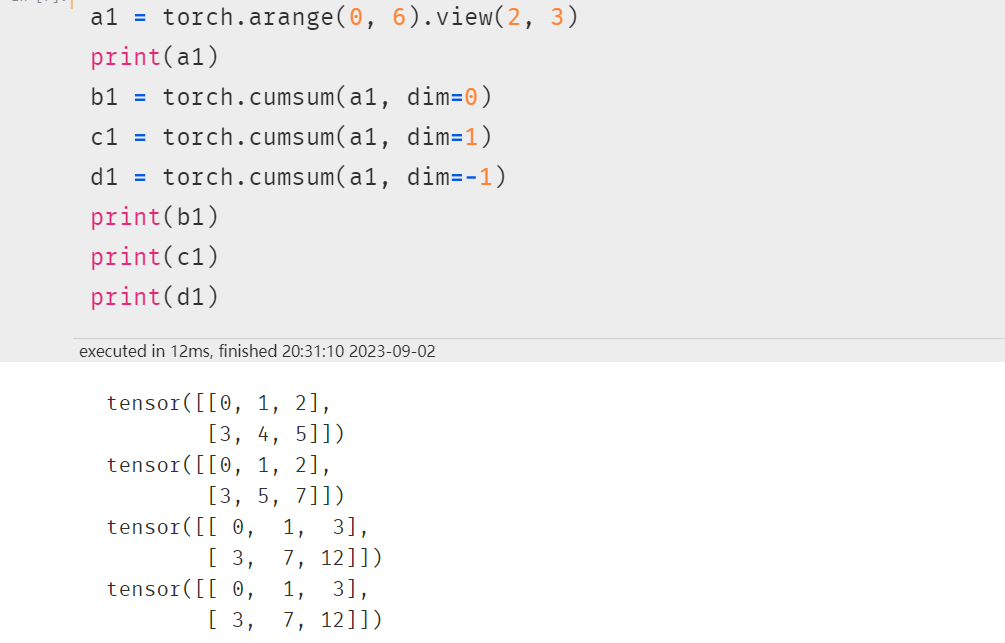
dim=0表示按行的方向滑动窗口来累计；dim=1/-1都表示按列的方向来滑动窗口来累计。
可以看到，操作之后规模/形状是不变的。
torch.cumprod：返回维度dim中输入元素的累计乘积。

torch.cummax、torch.cummin（注意输出有values和indices，若不指定则都输出）

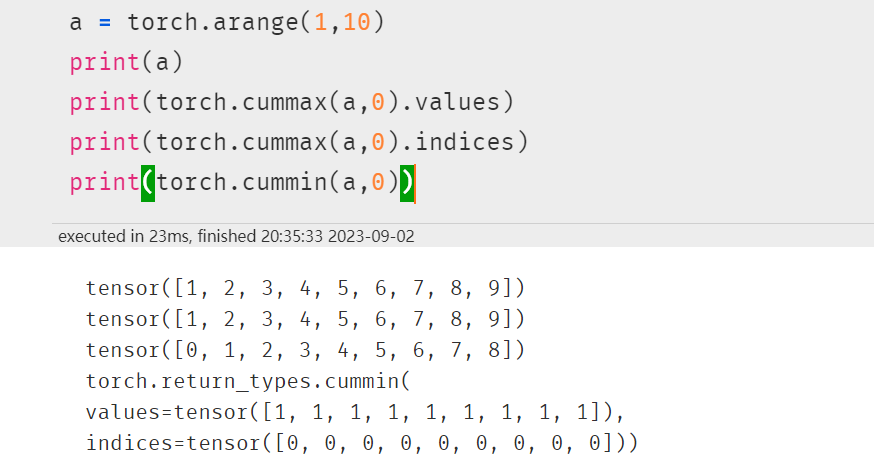
2. torch.sort torch.topk排序

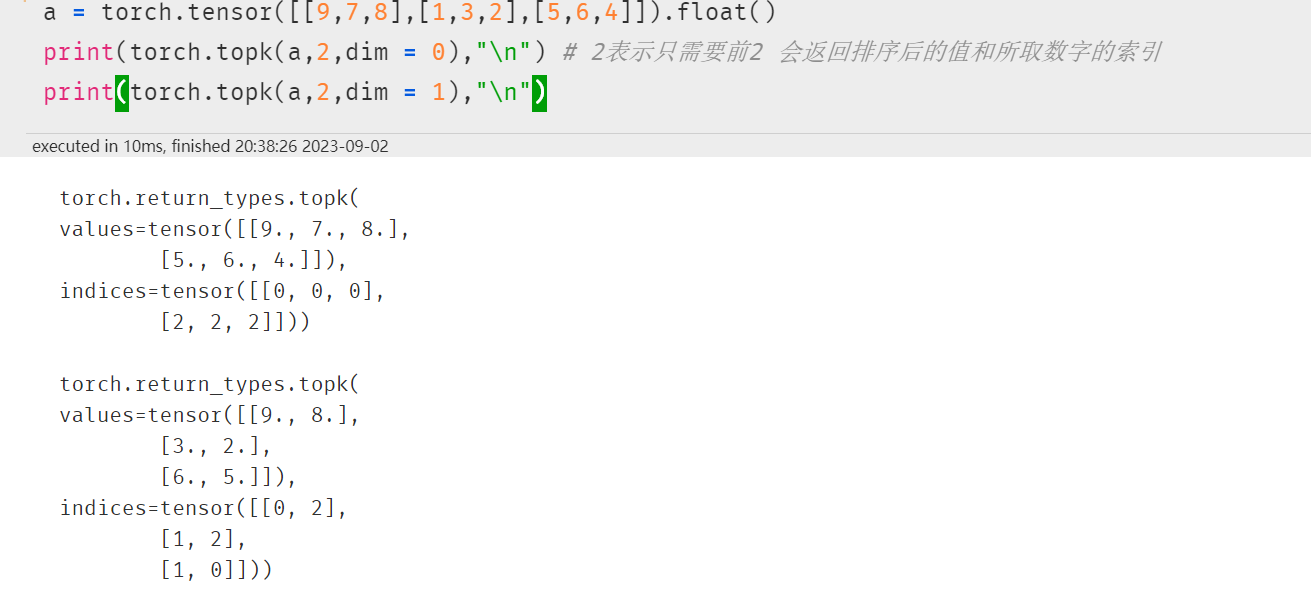
更改参数：（因为名字就是top k ）

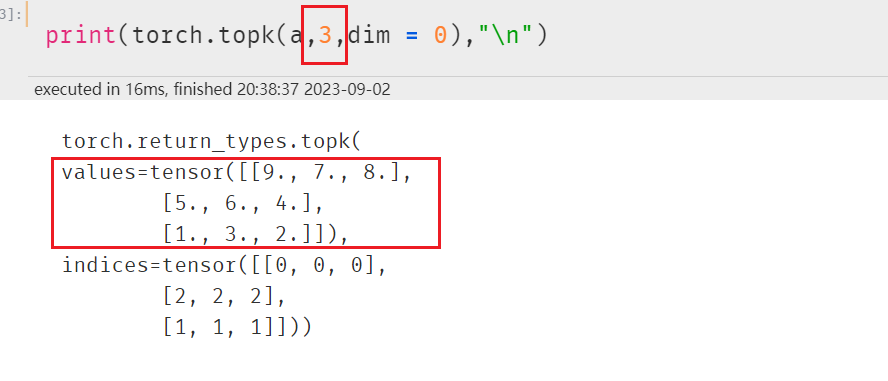
torch.sort 默认是从小到大

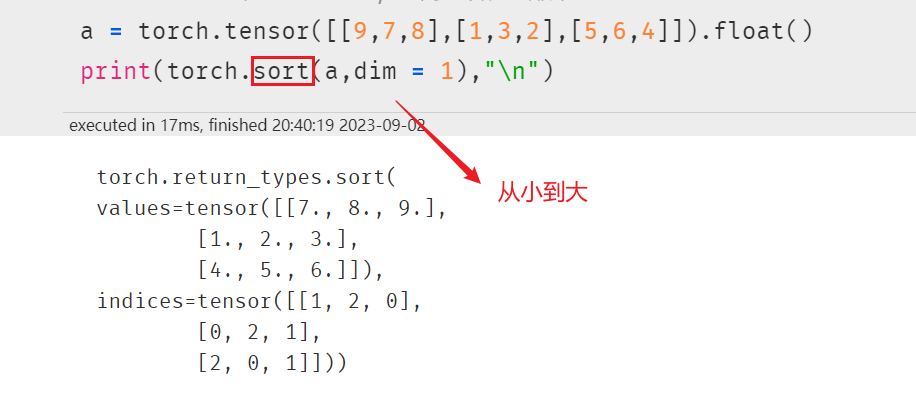
三、矩阵运算（操作的张量至少是二维张量）

矩阵必须是二维的。类似torch.tensor([1,2,3])这样的不是矩阵。
矩阵运算包括：矩阵乘法，矩阵逆，矩阵求迹，矩阵范数，矩阵行列式，矩阵求特征值，矩阵分解等运算。

1. 矩阵乘法

@ 符，等价于torch.matmul(a,b) 或 torch.mm(a,b)
*注意区分 * 和 @ 表示对应元素相乘


5x5x6 @ 5x6x4 = 5x5x4（后面两个维度相乘）

2. 矩阵转置

3. 矩阵求逆

4. 矩阵求迹

5. 矩阵求范数

6. 矩阵行列式

7. 矩阵求特征值和特征向量

8. 矩阵QR分解

矩阵QR分解, 将一个方阵分解为一个正交矩阵q和上三角矩阵r
QR分解实际上是对矩阵a实施Schmidt正交化得到q

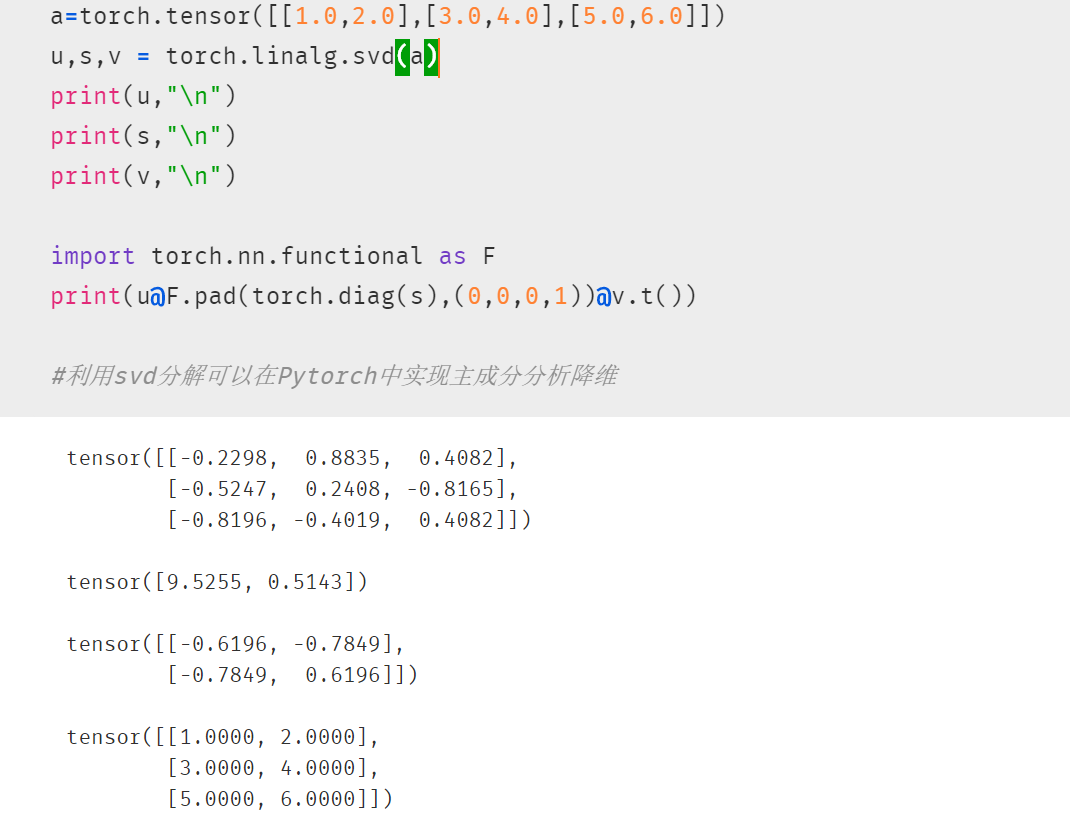
9. 矩阵SVD分解

svd分解可以将任意一个矩阵分解为一个正交矩阵u,一个对角阵s和一个正交矩阵v.t()的乘积
svd常用于矩阵压缩和降维

四、任意张量运算（einsum！！！）

如果问pytorch中最强大的一个数学函数是什么？
我会说是torch.einsum：爱因斯坦求和函数。
它几乎是一个"万能函数"：能实现超过一万种功能的函数。
不仅如此，和其它pytorch中的函数一样，torch.einsum是支持求导和反向传播的，并且计算效率非常高。
einsum 提供了一套既简洁又优雅的规则，可实现包括但不限于：内积，外积，矩阵乘法，转置和张量收缩（tensor contraction）等张量操作，熟练掌握 einsum 可以很方便的实现复杂的张量操作，而且不容易出错。
尤其是在一些包括batch维度的高阶张量的相关计算中，若使用普通的矩阵乘法、求和、转置等算子来实现很容易出现维度匹配等问题，若换成einsum则会特别简单。
套用一句深度学习paper标题当中非常时髦的话术，einsum is all you needed 😋！

1. einsum规则原理

这个函数的规则原理非常简洁，3句话说明白。
1，用元素计算公式来表达张量运算。
2，只出现在元素计算公式箭头左边的指标叫做哑指标。
3，省略元素计算公式中对哑指标的求和符号。

2. einsum基础范例

einsum这个函数的精髓实际上是第一条:
用元素计算公式来表达张量运算。
而绝大部分张量运算都可以用元素计算公式很方便地来表达，这也是它为什么会那么神通广大。

2.1 张量转置

转置后面两个维度

2.2 取对角元素

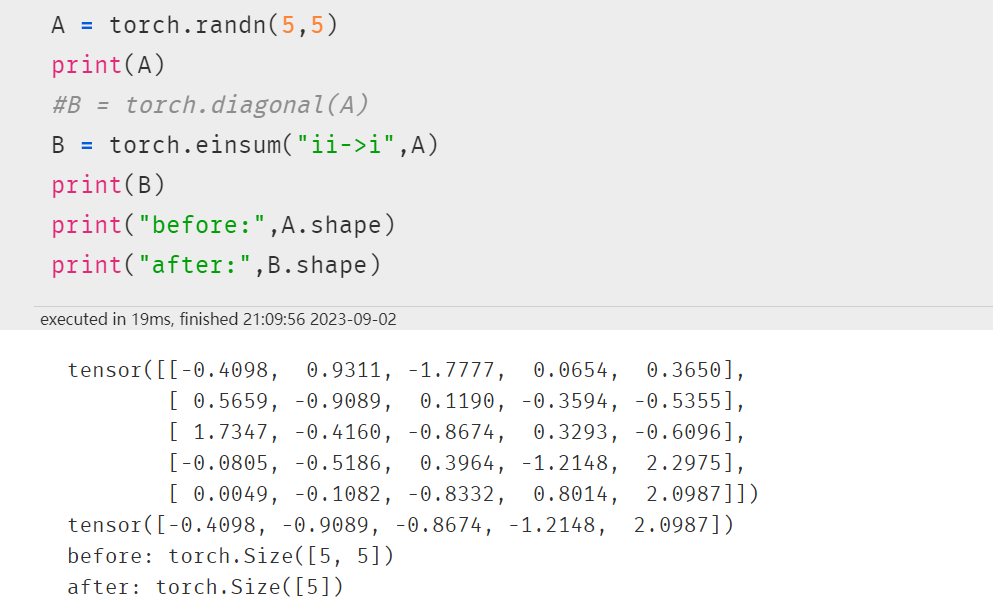
2.3 求和降维

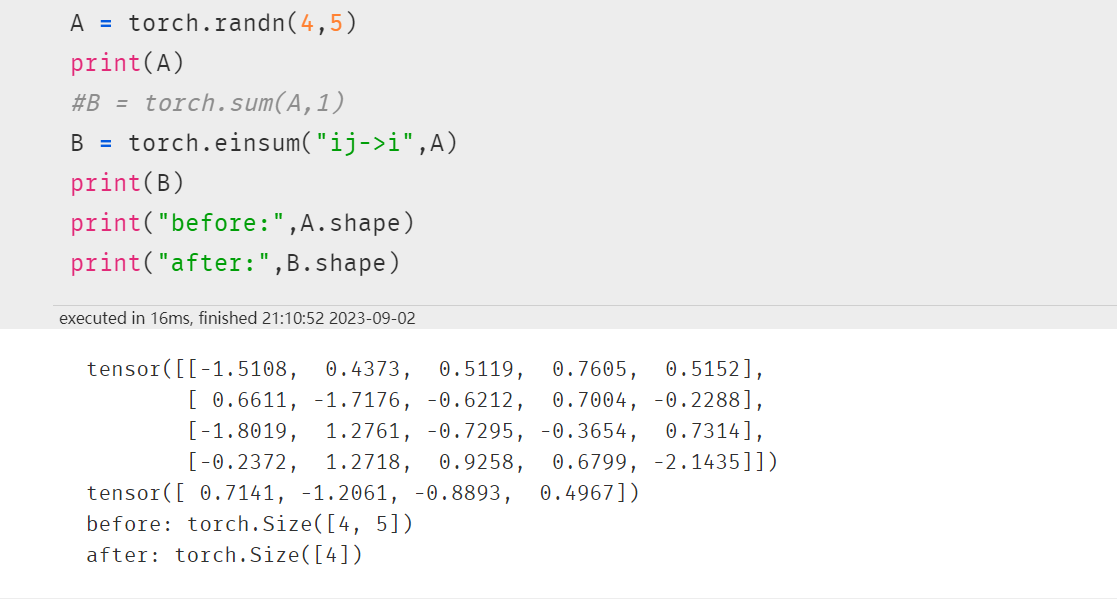
2.4 哈达玛积 各元素对应相乘

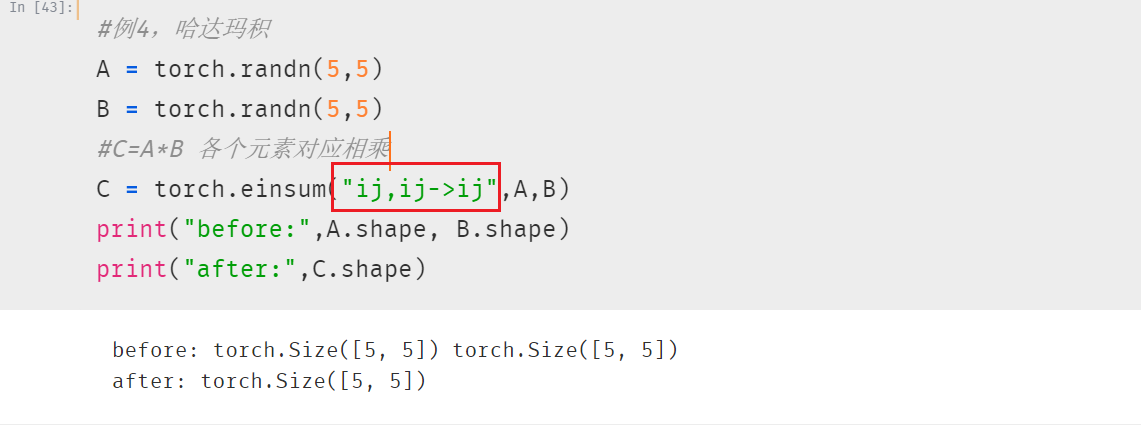
2.5 向量内积

注意 i,i-> 和 i,i->i 不一样！！！
向量内积得到的是一个数

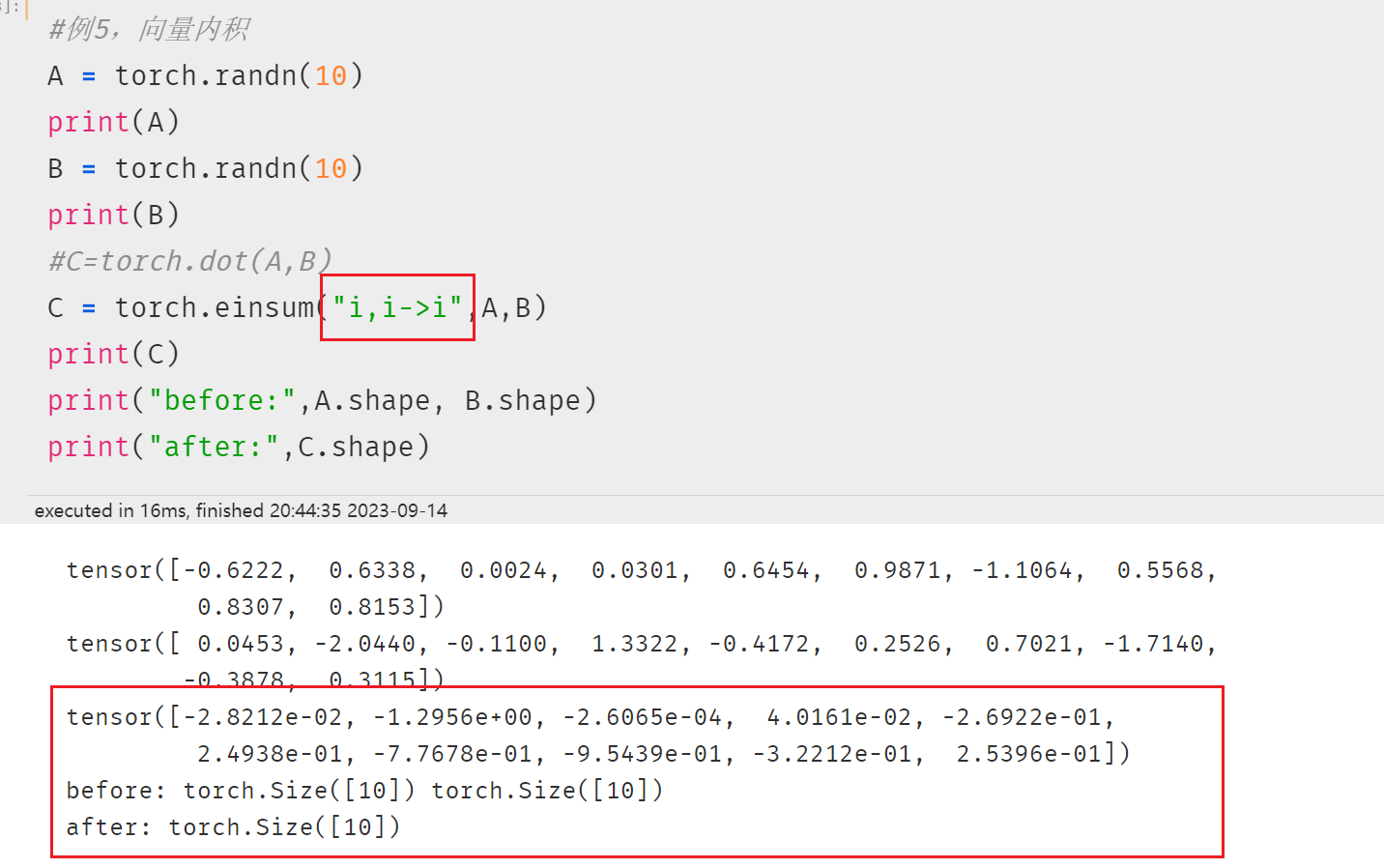
此处得到的还是与原来一致的大小。

2.6 向量外积

类似笛卡尔积

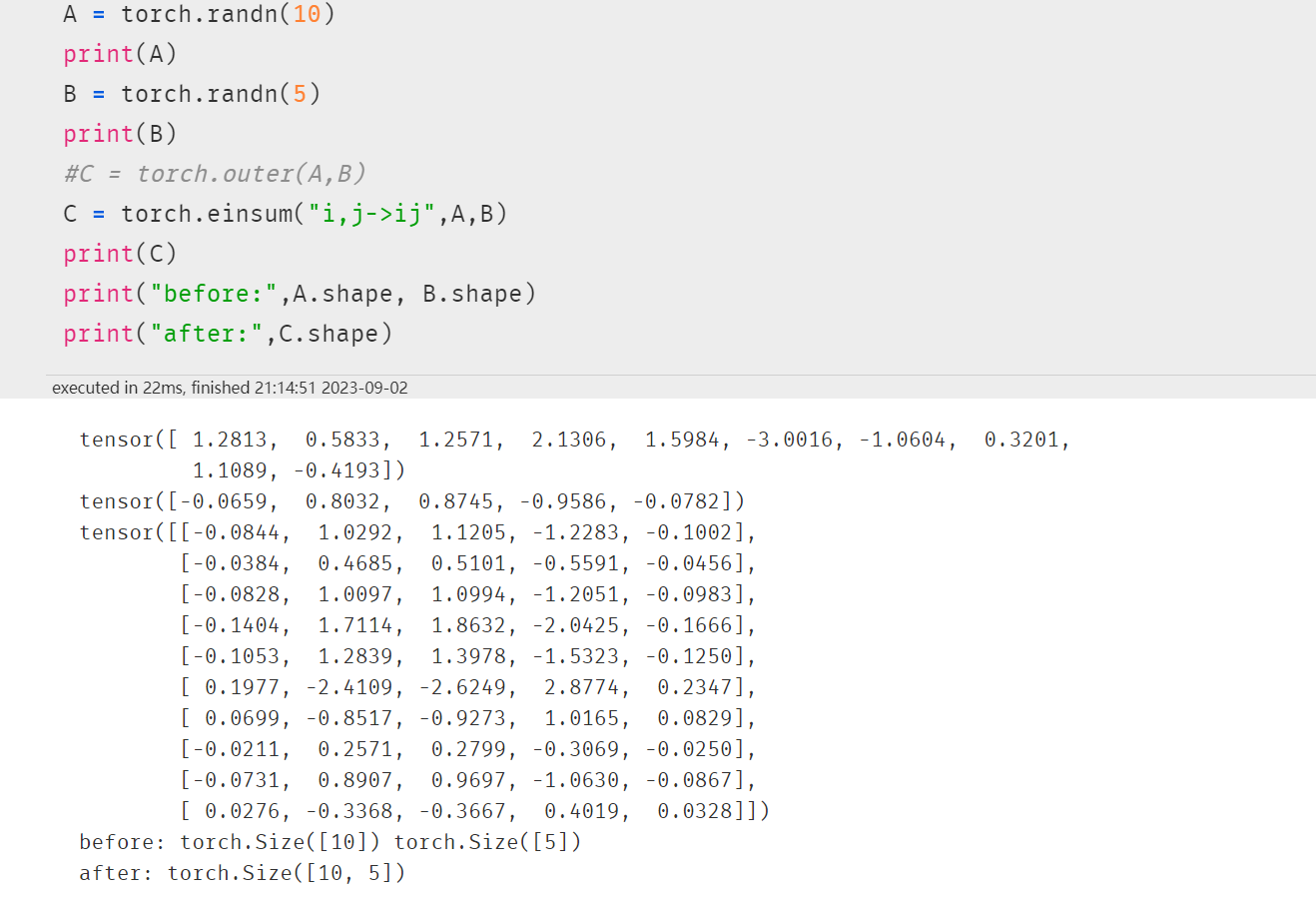
就是A中10个元素与B中5个元素相乘（所以enisum写法也是：i,j->ij），比如A的第1个元素与B的每个元素相乘，得到第一行数据，共5个值，最终矩阵是10x5

2.7 矩阵乘法

2.8 张量缩并

3. einsum高级范例

3.1 双线性变换

einsum可用于超过两个张量的计算。
例如：双线性变换。这是向量内积的一种扩展，一种常用的注意力机制实现方式)
不考虑batch维度时，双线性变换的公式如下：


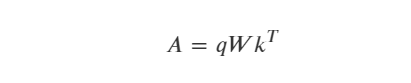
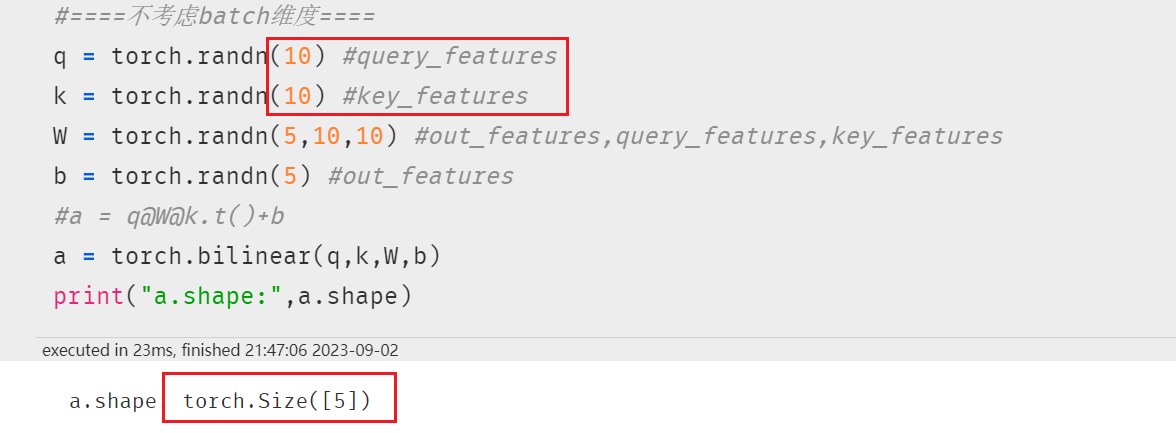
考虑batch维度时，无法用矩阵乘法表示，可以用元素计算公式表达如下：

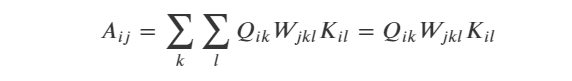
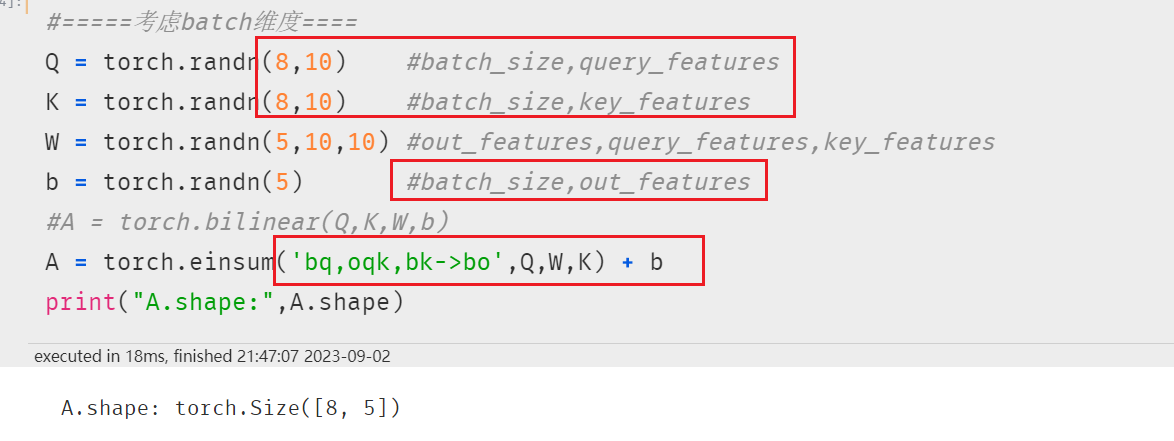
3.2 scaled-dot-product注意力机制

我们也可以用einsum来实现更常见的scaled-dot-product 形式的 Attention.
不考虑batch维度时，scaled-dot-product形式的Attention用矩阵乘法公式表示如下:


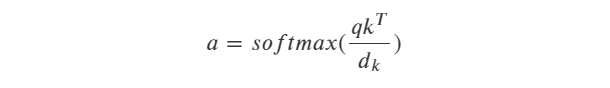
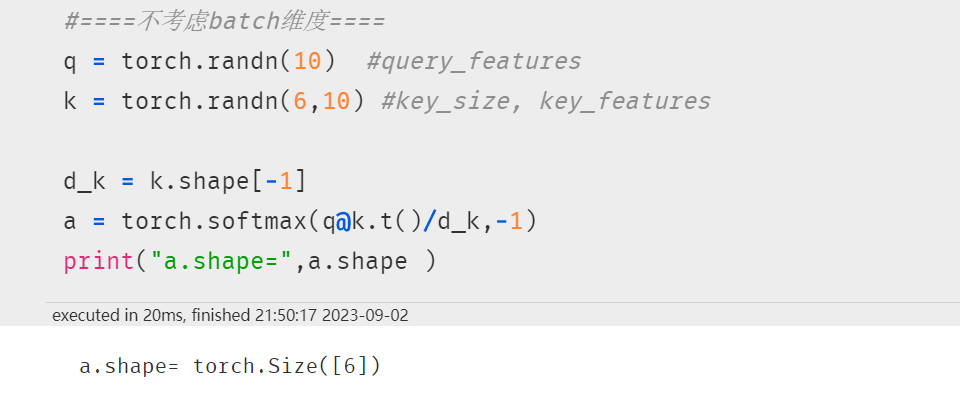
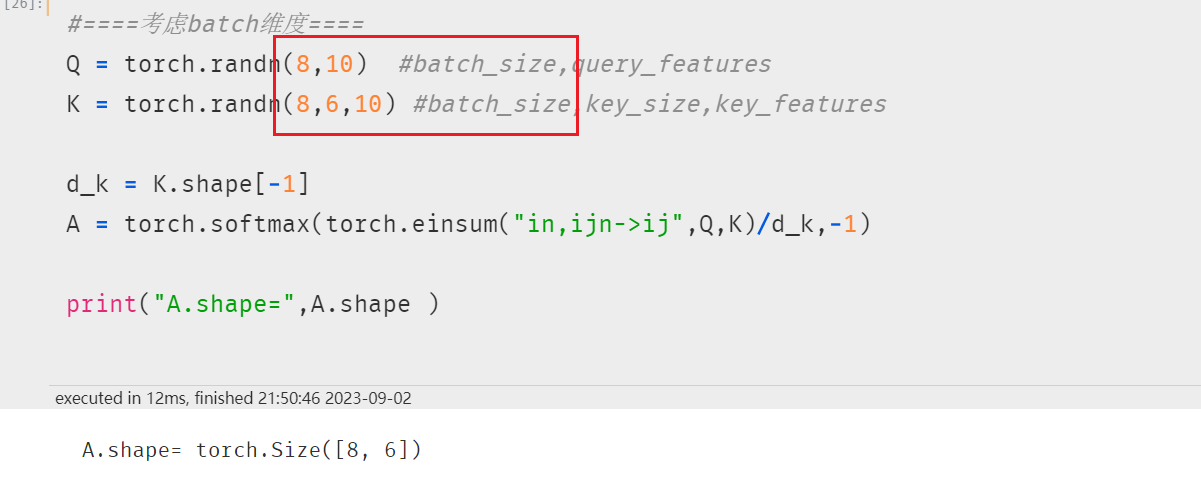
考虑batch维度时，无法用矩阵乘法表示，可以用元素计算公式表达如下：

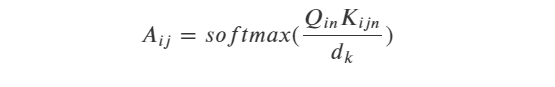
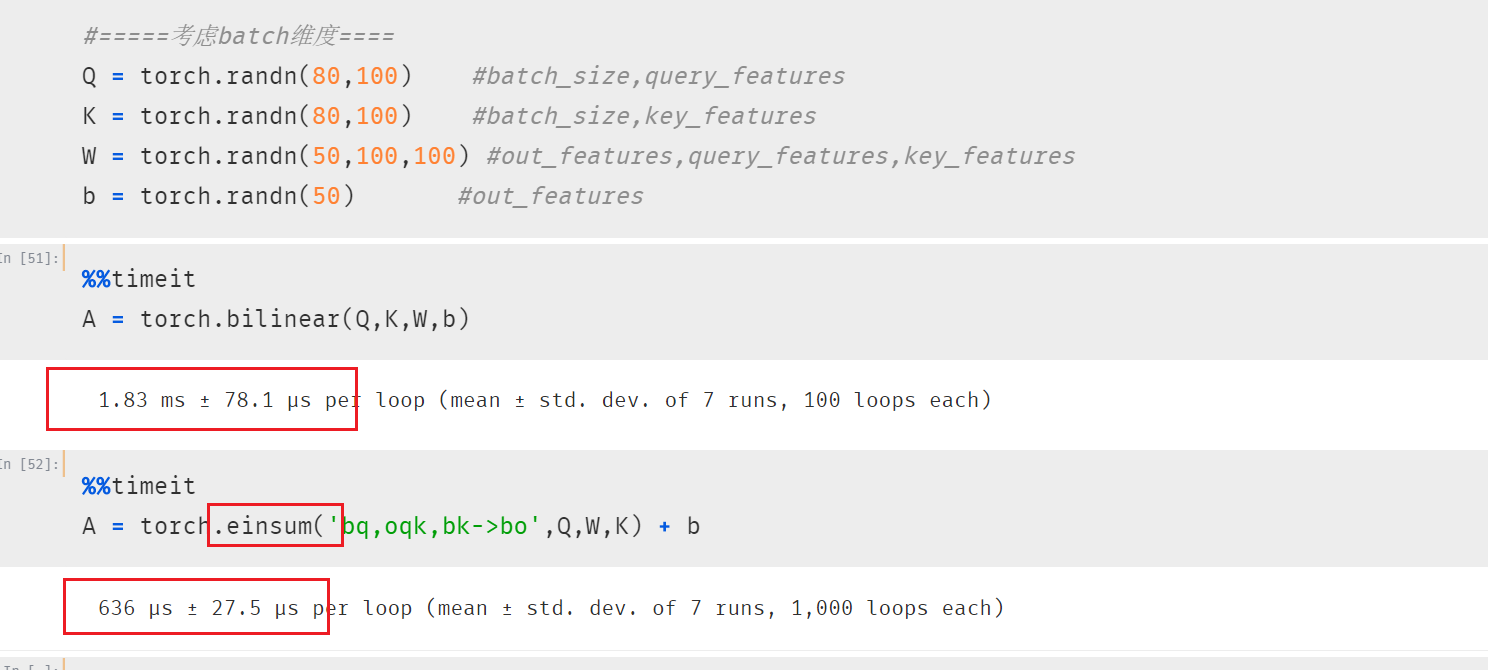
3.3 性能测试

五、广播机制

Pytorch的广播规则和numpy是一样的：
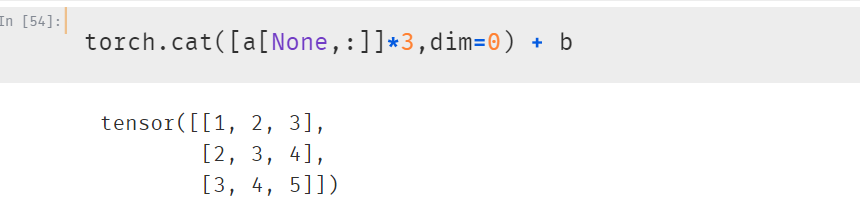
1、如果张量的维度不同，将维度较小的张量进行扩展，直到两个张量的维度都一样。

等价于：


2、如果两个张量在某个维度上的长度是相同的，或者其中一个张量在该维度上的长度为1，那么我们就说这两个张量在该维度上是相容的。
3、如果两个张量在所有维度上都是相容的，它们就能使用广播。
4、广播之后，每个维度的长度将取两个张量在该维度长度的较大值。
5、在任何一个维度上，如果一个张量的长度为1，另一个张量长度大于1，那么在该维度上，就好像是对第一个张量进行了复制。
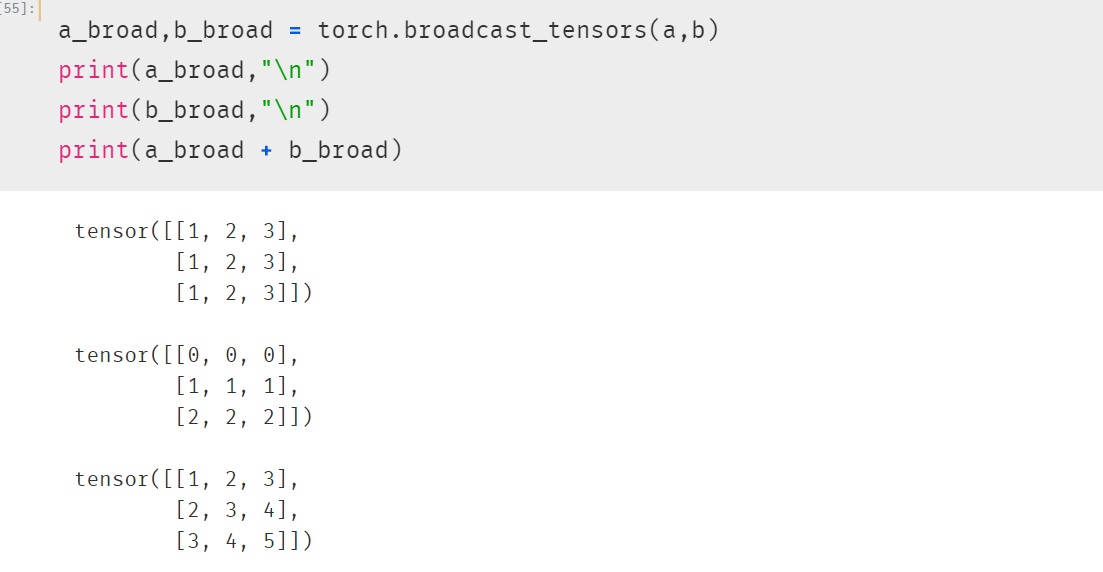
torch.broadcast_tensors可以将多个张量根据广播规则转换成相同的维度。
维度扩展允许的操作有两种： 1，增加一个维度 2，对长度为1的维度进行复制扩展

参考：https://github.com/lyhue1991/eat_pytorch_in_20_days