1 裁刀半径补偿问题的提出
偏心裁刀一般皮革和纸箱行业用的比较多,它适用于裁切比较厚的材料。对于如图1所示的偏心裁刀,它的刀尖和旋转轴(也就是刀心)存在一个距离,设为半径r。由于改刀刀刃有方向,所以用该刀去切割直线时,必须保证刀的角度方向与直线一致,否则会导致材料的损坏,裁刀切向跟随就是要保证切割直线时裁刀方向转到与直线方向一致。
用该刀去切割直线时,上位机发下来的plt指令是刀心的轨迹,但是由于存在半径距离r,所以刀心走的轨迹和刀尖切割的轨迹会有偏差,图2是不加补偿时切割的正方形和三角形。

偏心裁刀

未加补偿时正方形切割效果

未加补偿时三角形切割效果
2 裁刀半径补偿原理
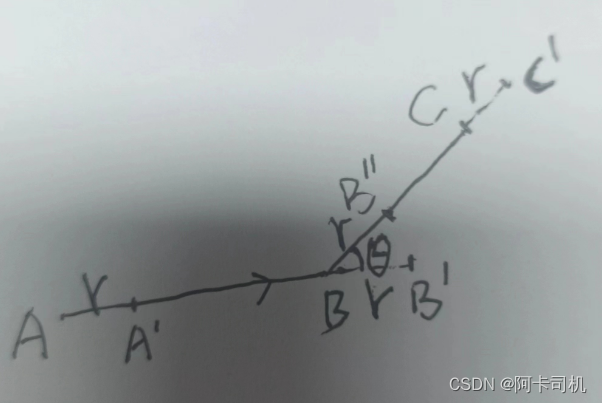
半径补偿原理示意图
如上图所示,切割俩条相邻线段AB和BC,它们的夹角为θ。则刀尖从A切到B,刀心走的轨迹是从A'走到B'。AA'和BB'长度都等于半径r。切第二段BC直线时,刀心必须先从B'走到B'',,然后再走直线B''C’。其中BB''和CC'的长度都为r。
当夹角θ比较大时,需要先抬刀,让刀心先走到B'',然后再下刀从B''走到C'。当夹角θ比较小时,这个时候不用抬刀,而是让刀沿着刀心转动角度θ与BC平行,同时控制XY电机让刀心走直线B'B''。注意,刀轴旋转θ运动和走直线B'B''运动必须同时进行,这样对纸张的损害比较小,同时切割运动也会比较流畅。
对于切割正方形三角形,直线转角比较大,需要在转角处抬刀。对于切割曲线,由于上位机发下来的拟合小线段之间夹角比较小,此时不抬刀并使用三轴联动方式进行线段过渡。
3 裁刀补偿实际切割实例
下面俩图是用本算法切割正方形和三角形时圆心运动轨迹示意图。大家可以比较一下这个示意图和第1节的未加补偿时的切割效果的区别。
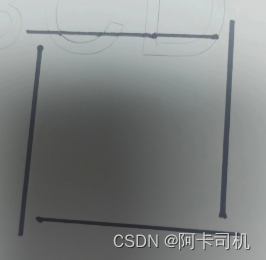
加补偿切正方形时刀心轨迹

加补偿切三角形时刀心轨迹
下面是使用裁刀半径补偿算法切割正方形、三角形和字母ABCD的效果。

加了补偿的正方形切割效果

加了补偿后三角形切割效果

加补偿后字母切割效果