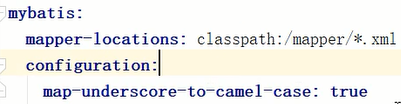
前言

常见的一些疑问:

1. 水平放置时，imu的z轴的值是正值，难道imu的z轴是朝下？
2. 水平往前倾，根据各轴的读数值，觉得imu的坐标系难道是左手系？

基于以上两个疑问，下面我将按我的理解解释一下。

解释

1. 假设模型
   我们假设imu的Z轴设计为如下简图:
   
   在带有imu的设备进行加减速运动时，图中的质量块由于受到惯性力作用而上下移动，该过程可通过一些物理参数的变化检测出来，从而算出此时所受的加速度大小。

2. 有意思的现象
   在静止时，由于质量块受到重力影响，会往下移动，但当我们沿着z轴方向加速移动imu时，此时滑块也会往下移动，因此重力的影响可以等价为imu检测到一个沿着重力反方向大小为g的加速度。

3. imu每个轴的值是如何计算的
   我们假设一个带有imu的物体在大地坐标系下按加速度 $\mathbf{a}=(a_x,a_y,a_z{)}^T$ 进行加速运动，并且imu与大地坐标系之间的旋转外参为 ${\mathbf{R}}_{bw}$。由于重力影响，结合第2步的等价关系，imu在大地坐标系下还受到一个加速度 $\mathbf{g}=(0,0,g{)}^T$ 的影响，g为正值。因此，最后imu的加速度计的测量值为:
   $${\mathbf{a}}_m={\mathbf{R}}_{bw}(\mathbf{a}+\mathbf{g})$$

4. 回答问题1
   结合第3步公式可知，当imu水平放置时，${\mathbf{R}}_{bw}=\mathbf{I}$、$\mathbf{a}=(0,0,0{)}^T$，此时测量值就等于 $(0,0,g{)}^T$ ，z轴为正值，并且等于重力加速度大小g。

5. 回答问题2
   由于我们可以轻易通过重力在x轴和y轴的分量来确定x轴和y轴，唯一存在争议的是z轴，第4步解释了z轴朝上时，静止情况下z轴的读数为正值，基于此可以确定出z轴方向，三个方向确定后即可明确imu坐标系为右手系。