*下文中“优于”一般指的是“不劣于”，请自行分辨。

四边形不等式

四边形不等式定义为：
位于整数集合上的二元函数$f(x,y)$，对于$a\le b\le c\le d$，若满足：$f(a,c)+f(b,d)\le f(a,d)+f(b,c)$，即相交和小于包含和，则称函数$f$满足四边形不等式。

函数$f$若满足$f(a,c)+f(b,d)\le f(a,d)+f(b,c)$，即相交和大于包含和，则亦称函数$f$满足四边形不等式。

在动态规划问题中，四边形不等式指的是相交优于包含（可能是大于，也可能是小于），因为相交优于包含能够推出决策单调性。接下来讨论相交小于包含。

四边形不等式具有两种等价的定义：

1. $a\le b\le c\le d:f(a,c)+f(b,d)\le f(a,d)+f(b,c)$
2. $f(i,j)+f(i+1,j+1)\le f(i,j+1)+f(i+1,j)$

下面是证明。

还原不等式

接下来展示一种用来推式子的方法。主要思想就是根据条件列出一个不等式，然后把结论写成另一个不等式。通过对比发现从条件到结论差了什么，然后把差的那部分还原出来。

我们证明一下从2推出1，记$f(x,y)=f_{x,y}$：

首先我们归纳，假设对于所有的长度小于$j-i+2$的区间都满足“从2可以推出1”的结论：

我们已知$f_{i,j}+f_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}①$

要证明$f_{i,c}+f_{b,j+1}\le f_{i,j+1}+f_{b,c}(i\le b\le c\le j+1)$

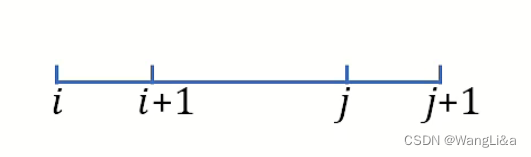
现在我们设法让式子中的$i+1$变为$i+2$：
$f_{i,j}+f_{i+2,j+1}\le f_{i,j+1}+f_{i+2,j}②$

然后我们对比一下条件①和要证明的式子②：
$①:f_{i,j}+f_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}$
$②:f_{i,j}+f_{i+2,j+1}\le f_{i,j+1}+f_{i+2,j}$

两式有一些项是相同的，有一些项是不同的，不同的项用颜色标出来了。我们假设有一个不等式$T$，使得$①+T=②$，现在我们试图还原出$T$来：
$①:f_{i,j}+f_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}$
$T:?\le ?$
$②:f_{i,j}+f_{i+2,j+1}\le f_{i,j+1}+f_{i+2,j}$

可以看到相同的项同时在①、②式中出现，因此在$T$中不需要管他们。
蓝色的项在②式中出现，而在①式中没有，因此应该在$T$中被加上去，所以我们把蓝色的项写到$T$不等号的对应侧：

$①:f_{i,j}+f_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}$
$T:?+f_{i+2,j+1}\le ?+f_{i+2,j}$
$②:f_{i,j}+f_{i+2,j+1}\le f_{i,j+1}+f_{i+2,j}$

可以看到红色的项原来在①中出现了，但是在②中消失了，这说明它们在$T$中被减去了一次，也就是说带有负一的系数：

$①:f_{i,j}+f_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}$
$T:-f_{i+1,j+1}+f_{i+2,j+1}\le -f_{i+1,j}+f_{i+2,j}$
$②:f_{i,j}+f_{i+2,j+1}\le f_{i,j+1}+f_{i+2,j}$

整理一下$T$：
$T:f_{i+2,j+1}+f_{i+1,j}\le f_{i+2,j}+f_{i+1,j+1}$

这恰好就是区间长度为$j-i+1$的四边形不等式，因此$①+T=②$，则②式得证。

至此，我们已经可以仿照刚才的证明，将四边形不等式内部的两个端点向内移动1的长度任意次，因此我们已经证明了$f_{i,c}+f_{b,j+1}\le f_{i,j+1}+f_{b,c}(i\le b\le c\le j+1)$

QED.

石子合并

这篇文章只涉及简单四边形不等式优化dp，因此最优决策点都是枚举的。

石子合并求最小值

设$a_i$表示第$i$堆石子的大小。

首先破环为链，然后区间dp：

设状态函数$f_{i,j}$为区间$[i,j]$对应的石子合并成一堆的最小贡献，$s$表示石子的前缀和。

则： f i , j = min ⁡ k = i j { f i , k + f k + 1 , j } + s j − s i − 1 f_{i,j}=\overset{j}{\underset{k=i}{\min}}\left\{f_{i,k}+f_{k+1,j}\right\}+s_j-s_{i-1} fi,j​=k=imin​j​{fi,k​+fk+1,j​}+sj​−si−1​

这里其实$k$应该枚举到$j-1$就停止的，那我们拓展一下状态，令$f_{x+1,x}=-\infty$

暴力区间dp是$O(n^3)$的：

  for(int len=2;len<=n;len++){            区间长度
    for(int i=1,j;(j=i+len-1)<=2*n;i++){  区间端点
      for(int k=i;k<j;k++){               区间分割点
        f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
      }
    }
  }

可以优化到$O(n^2)$：

  for(int len=2; len<=n; len++){               区间长度
    for(int i=1,j; (j=i+len-1)<=2*n; i++){     区间端点
      for(int k=p[i][j-1]; k<=p[i+1][j]; k++){ 区间分割点
        if(f[i][j]>f[i][k]+f[k+1][j]+s[j]-s[i-1]) 决策单调性优化dp
          f[i][j]=f[i][k]+f[k+1][j]+s[j]-s[i-1], p[i][j]=k;
      }
    }
  }

大概的意思是说设$p_{i,j}$表示$f_{i,j}$的最优决策点，则$p_{i,j-1}\le p_{i,j}\le p_{i+1,j}$，我们通过把枚举决策点的区间缩小，减小了复杂度。

接下来用四步我们来看看这个过程：

1. 证明贡献函数$w_{i,j}$满足四边形不等式
2. 证明状态函数$f_{i,j}$满足四边形不等式
3. 证明决策单调性。
4. 证明时间复杂度$O(n^2)$

1.证明贡献函数满足四边形不等式

四边形不等式

对于： f i , j = min ⁡ k = i j { f i , k + f k + 1 , j } + s j − s i − 1 f_{i,j}=\overset{j}{\underset{k=i}{\min}}\left\{f_{i,k}+f_{k+1,j}\right\}+s_j-s_{i-1} fi,j​=k=imin​j​{fi,k​+fk+1,j​}+sj​−si−1​

我们定义贡献函数$w_{i,j}=s_j-s_{i-1}(w_{i,i}除外)$，也就是说：
f i , j = min ⁡ k = i j { f i , k + f k + 1 , j } + w i , j f_{i,j}=\overset{j}{\underset{k=i}{\min}}\left\{f_{i,k}+f_{k+1,j}\right\}+w_{i,j} fi,j​=k=imin​j​{fi,k​+fk+1,j​}+wi,j​

其中$f_{i,i}=0,w_{i,i}=0$

接下来证明$w$满足四边形不等式：
$w_{i,j}+w_{i+1,j+1}\le w_{i,j+1}+w_{i+1,j}$
即：$s_j-s_{i-1}+s_{j+1}-s_i\le s_{j+1}-s_{i-1}+s_j-s_i$

左右两边直接相等了，所以肯定满足四边形不等式…

区间包含单调性

事实上，显然贡献函数还满足区间包含单调性：
$w_{x,y}\le w_{i,j}([x,y]\subseteq [i,j])$

贡献数量

设$f_{i,j}=\stackrel{j-i}{\sum _{k=1}}{w}_{x_k,y_k}$，则满足$[x_k,y_k]\subseteq [i,j]$

证明：
初始状态中，区间$[i,j]$中有$j-i+1$堆石子，每进行一次操作就会减少一堆石子，同时给$f_{i,j}$增加一个$w_{x,y}$，其中$[x,y]\subseteq [i,j]$，总共最后合并到只有一堆石子，总共合并了$j-i$次，因此状态函数贡献了$j-i$个，证毕。

上界

$f_{i,j}\le (j-i)\cdot w_{i,j}$

证明：
因为：$w_{x_k,y_k}\le w_{i,j}$
所以：$f_{i,j}=\stackrel{j-i}{\sum _{k=1}}{w}_{x_k,y_k}\le (j-i)\cdot w_{i,j}$

2.证明状态函数满足四边形不等式

证明$f_{i,j}+f_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}$：

首先归纳一下，假设对于所有区间长度小于$j-i+2$的区间都满足状态函数上的四边形不等式。

然后我们设$f_{i,j+1}$的最优决策点为$x$。
$f_{i,j+1}=f_{i,x}+f_{x+1,j+1}+w_{i,j+1}$

我们知道$f_{i,j}$的最优决策点不一定为$x$，因此有不等式：
$f_{i,j}\le f_{i,x}+f_{x+1,j}+w_{i,j}$

同理，我们设$f_{i+1,j}$为$y$，则：$f_{i+1,j}=f_{i+1,y}+f_{y+1,j}+w_{i+1,j}$
考虑$f_{i+1,j+1}$的最优决策点不一定为$y$，就得到：$f_{i+1,j+1}\le f_{i+1,y}+f_{y+1,j+1}+w_{i+1,j+1}$

为了凑出$f_{i,j}+f_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}$，我们需要把刚才的四个式子加起来（注意等式相加的方向）：
$f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}+w_{i,j+1}+w_{i+1,j}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}+w_{i,j}+w_{i+1,j+1}$

因此现在距离要证明的结论已经相当接近了，要想办法约掉剩余的几项。

先看到贡献函数$w$：
$f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}+w_{i,j+1}+w_{i+1,j}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}+w_{i,j}+w_{i+1,j+1}$

可以对左边用四边形不等式$w_{i,j}+w_{i+1,j+1}\le w_{i,j+1}+w_{i+1,j}$（也可以对右边用）：
$$\begin{gathered} f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}+w_{i,j}+w_{i+1,j+1}\le f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}+w_{i,j+1}+w_{i+1,j}\le \\ {f}_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}+w_{i,j}+w_{i+1,j+1} \end{gathered}$$

然后我们研究左右那两项：
$f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}+w_{i,j}+w_{i+1,j+1}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}+w_{i,j}+w_{i+1,j+1}$

就把贡献函数约掉了：
$f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}$

现在我们来研究多余的那四项状态函数：
$f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}$

• 若$x\le y$，则红色两项不交，蓝色的两项则是包含关系，就会有$f_{x+1,j}+f_{y+1,j+1}\le f_{x+1,j+1}+f_{y+1,j}$，因此就会有：
  $f_{i,j}+f_{i+1,j+1}+f_{x+1,j}+f_{y+1,j+1}\le f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}$
  去掉中间那个式子：$f_{i,j}+f_{i+1,j+1}+f_{x,j}+f_{y+1,j+1}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}$

• 若$x>y$，则蓝色两项不交，红色两项则是相交关系，就会有$f_{x+1,j}+f_{y+1,j+1}\le f_{x+1,j+1}+f_{y+1,j}$，因此就会有：
  $f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j}+f_{y+1,j+1}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j+1}+f_{y+1,j}$
  去掉中间那个式子：
  $f_{i,j}+f_{i+1,j+1}+f_{x+1,j+1}+f_{y+1,j}\le f_{i,j+1}+f_{i+1,j}+f_{x+1,j+1}+f_{y+1,j}$

可以看出无论那种情况，红蓝两项都抵消了，因此得证。
（一些什么边界情况就不考虑的了，反正显然）

后记：

• 至于是把$x,y$是应该带入$f_{i,j},f_{i+1,j+1}$还是应该带入$f_{i+1,j+1},f_{i,j}$，没有区别，很明显这两种情况是对称的。
• 至于如果有人问如果$x,y$不表示$f_{i,j+1},f_{i+1,j}$的最优决策点，表示$f_{i,j},f_{i+1,j+1}$的最优决策点行不行，答案是不行，因为不等号方向反了。
• 感觉这种推导还是应该从条件和结论的联系上找线索。还是双向奔赴会比较容易…其实这种证明过程一般情况下结论比条件好确定…

3.证明决策单调性

设$p_{i,j}$表示$f_{i,j}$的其中一个最优决策点。

决策单调性指的是，$\forall p_{i,j-1},p_{i+1,j}:\exists p_{i,j}满足p_{i,j-1}\le p_{i,j}\le p_{i+1,j}$

左边

先证明左半部分：
$p_{i,j-1}\le p_{i,j}$，设$k=p_{i,j-1},p=p_{i,j}$，则我们反证，设$p<k$：

一开始可以认为我们的条件有四个式子：
$\{\begin{array}{c}①:f_{i,j}=f_{i,p}+f_{p+1,j}+w_{i,j}\\ ②:f_{i,j-1}=f_{i,k}+f_{k+1,j-1}+w_{i,j-1}\\ ③:f_{i,j}\le f_{i,k}+f_{k+1,j}+w_{i,j}\\ ④:f_{i,j-1}\le f_{i,p}+f_{p+1,j-1}+w_{i,j-1}\end{array}$

然后我们为了导出矛盾，可能会有两个式子：
$\{\begin{array}{c}A:f_{i,j-1}>f_{i,p}+f_{p+1,j-1}+w_{i,j-1}\\ B:f_{i,j}\ge f_{i,k}+f_{k+1,j}+w_{i,j}\end{array}$
其中$A$矛盾叫做：“$k$不是$f_{i,j-1}$的最优决策点”。（注意，这里如果证明$p$与$k$对于$f_{i,j-1}$一样优并不能导出矛盾，因为最优决策点并不一定唯一）
其中$B$矛盾叫做：“$k$也是$f_{i,j}$的最优决策点”。（因为综合条件③和$B$能够知道，$f_{i,j}=f_{i,k}+f_{k+1,j}+w_{i,j}$，说明$k$也是$f_{i,j}$的最优决策点）

条件中没有大于号，很显然结论$B$更容易推导。

证法1

一种平凡的证法：

已知：$\{\begin{array}{c}①:f_{i,j}=f_{i,p}+f_{p+1,j}+w_{i,j}\\ ②:f_{i,j-1}=f_{i,k}+f_{k+1,j-1}+w_{i,j-1}\\ ③:f_{i,j}\le f_{i,k}+f_{k+1,j}+w_{i,j}\\ ④:f_{i,j-1}\le f_{i,p}+f_{p+1,j-1}+w_{i,j-1}\end{array}$

要证：$f_{i,j}\ge f_{i,k}+f_{k+1,j}+w_{i,j}$

首先是一番的推理：
首先因为最后一步已经用到了式③来证明$f_{i,j}=f_{i,k}+f_{k+1,j}+w_{i,j}$，可以假设之间没有用到式③…然后因为带有不等号，所以必定含有式④：
$f_{i,j-1}\le f_{i,p}+f_{p+1,j-1}+w_{i,j-1}$

然后因为还少了$f_{i,j},w_{i,j}$，我们可以把①的右边加④的左边，把左边加到右边，这样$f_{i,j}$与$w_{i,j}$的方向就对了，就得到：
$f_{i,j-1}+f_{i,p}+f_{p+1,j}+w_{i,j}\le f_{i,j}+f_{i,p}+f_{p+1,j-1}+w_{i,j-1}$
还约掉一项$f_{i,p}$：$f_{i,j-1}+f_{p+1,j}+w_{i,j}\le f_{i,j}+f_{p+1,j-1}+w_{i,j-1}$

没什么想法，先把②带入进去：
$f_{i,k}+f_{k+1,j-1}+w_{i,j-1}+f_{p+1,j}+w_{i,j}\le f_{i,j}+f_{p+1,j-1}+w_{i,j-1}$
又约掉一项$w_{i,j-1}$：$f_{i,k}+f_{k+1,j-1}+f_{p+1,j}+w_{i,j}\le f_{i,j}+f_{p+1,j-1}$

现在要想办法把右侧的$f_{p+1,j-1}$约掉，发现可以对左边用四边形不等式：
$f_{i,k}+f_{k+1,j-1}+f_{p+1,j}+w_{i,j}\le f_{i,j}+f_{p+1,j-1}$
$f_{i,k}+f_{k+1,j}+f_{p+1,j-1}+w_{i,j}\le f_{i,k}+f_{k+1,j-1}+f_{p+1,j}+w_{i,j}\le f_{i,j}+f_{p+1,j-1}$
$f_{i,k}+f_{k+1,j}+f_{p+1,j-1}+w_{i,j}\le f_{i,j}+f_{p+1,j-1}$

现在可以约掉$f_{p+1,j-1}$了：
$f_{i,k}+f_{k+1,j}+w_{i,j}\le f_{i,j}$

QED.

证法2

一种更有技巧性的证法：
已知：$\{\begin{array}{c}①:f_{i,j}=f_{i,p}+f_{p+1,j}+w_{i,j}\\ ②:f_{i,j-1}=f_{i,k}+f_{k+1,j-1}+w_{i,j-1}\\ ③:f_{i,j}\le f_{i,k}+f_{k+1,j}+w_{i,j}\\ ④:f_{i,j-1}\le f_{i,p}+f_{p+1,j-1}+w_{i,j-1}\end{array}$

要证：$f_{i,j}\ge f_{i,k}+f_{k+1,j}+w_{i,j}$

因为不等号方向不对，所以不能有③，因为式中有$w_{i,j}$，所以必须把①带进去，消掉$w_{i,j}$：
$f_{i,p}+f_{p+1,j}\ge f_{i,k}+f_{k+1,j}$
$f_{i,k}+f_{k+1,j}\le f_{i,p}+f_{p+1,j}$
（这是要证明的式子）
这个式子的意思就是在$f_{i,j}$意义下$k$比$p$优。

而我们知道在$f_{i,j-1}$意义下$k$比$p$优：$f_{i,k}+f_{k+1,j-1}\le f_{i,p}+f_{p+1,j-1}$

我们可以比较一下这两个式子：
$条件：f_{i,k}+f_{k+1,j-1}\le f_{i,p}+f_{p+1,j-1}$
$结论：f_{i,k}+f_{k+1,j}\le f_{i,p}+f_{p+1,j}$

若有：$条件+T=结论$，则$T:f_{p+1,j-1}+f_{k+1,j}\le f_{k+1,j-1}+f_{p+1,j}$，恰为四边形不等式，证毕。

因此我们知道$f_{i,j}\ge f_{i,k}+f_{k+1,j}+w_{i,j}$，而我们又知道$f_{i,j}\le f_{i,k}+f_{k+1,j}+w_{i,j}$，因此$f_{i,j}=f_{i,k}+f_{k+1,j}+w_{i,j}$。
这说明如果存在一个$p>k$，则$k$必然也是$f_{i,j}$的最优决策点，因此只需要枚举到$k$。

右边

接下来证明右边：

要证$p_{i,j}\le p_{i+1,j}$，设$p=p_{i,j},k=p_{i+1,j}$，就假设$p>k$。

我们仿照左边的思路，想要从“$f_{i+1,j}$意义下$k$更优”推出“$f_{i,j}$意义下$k$更优”。

想要证明$f_{i,j}\ge f_{i,k}+f_{k+1,j}+w_{i,j}$，即：
$结论:f_{i,k}+f_{k+1,j}\le f_{i,p}+f_{p+1,j}$

我们知道对于$f_{i+1,j}$来说，$k$优于$p$：
$条件:f_{i+1,k}+f_{k+1,j}\le f_{i+1,p}+f_{p+1,j}$

设：$条件+T=结论$，用还原不等式的方法求出$T$，$T$恰是四边形不等式。

4.证明时间复杂度

枚举决策点的总次数约为：
$\stackrel{n}{\sum _{len=1}}\stackrel{2n-len+1}{\sum _{i=1}}{p}_{i+1,i+len-1}-p_{i,i+len-2}+1$
$\le \stackrel{n}{\sum _{len=1}}\stackrel{2n}{\sum _{i=1}}{p}_{i+1,i+len-1}-p_{i,i+len-2}+1$
$=\stackrel{n}{\sum _{len=1}}\left(\stackrel{2n}{\sum _{i=1}}{p}_{i+1,i+len-1}-\stackrel{2n}{\sum _{i=1}}{p}_{i,i+len-2}\right)+n$
$=\stackrel{n}{\sum _{len=1}}\left(\stackrel{2n+1}{\sum _{i=2}}{p}_{i,i+len-2}-\stackrel{2n}{\sum _{i=1}}{p}_{i,i+len-2}\right)+n$
$=\stackrel{n}{\sum _{len=1}}{p}_{2n+1,2n+len-1}-p_{1,len-1}+n$
$=\stackrel{n}{\sum _{len=1}}O(n)$
$=O(n^2)$

转移复杂度为$O(1)$，因此证完。

石子合并求最大值

原来的代码：

 for(int len=2;len<=n;len++){             区间长度
    for(int i=1,j;(j=i+len-1)<=2*n;i++){  区间端点
      for(int k=i;k<j;k++){               区间分割点
        g[i][j]=max(g[i][j],g[i][k]+g[k+1][j]+s[j]-s[i-1]);
      }
    }
  }

新的代码：

  for(int len=2; len<=n; len++){               区间长度
    for(int i=1,j; (j=i+len-1)<=2*n; i++){     区间端点
      g[i][j]=max(g[i][j-1],g[i+1][j])+s[j]-s[i-1];
    }
  }

因为最大值的最优决策一定能在两端取得，也即：
g i , j = max ⁡ { g i , j − 1 , g i + 1 , j } + w i , j g_{i,j}=\max\{g_{i,j-1},g_{i+1,j}\}+w_{i,j} gi,j​=max{gi,j−1​,gi+1,j​}+wi,j​

证明

*请注意接下来证明中“左端”和“左侧”的区别，对于区间$[i,j]=[i,k]+[k+1,j]$，左端指的是$[i,i]$，而左侧指的是$[i,k]$

要证明最大值的最优决策一定会在两端取得，可以考虑$g_{i,j}$的最优决策，因此归纳所有区间长度小于$j-i+1$的区间全都符合假设：

反证，假设端点不是最优决策点（反论题），设最优决策点为$k(i<k<j-1)$，则：
$g_{i,j}=g_{i,k}+g_{k+1,j}+w_{i,j}$

现在考虑区间$g_{i,k}$，我们知道$g_{i,k}$的最优决策一定在其两端取得。假设在左端取得，则$g_{i,j}=g_{i+1,k}+w_{i,k}+g_{k+1,j}+w_{i,j}$

我们可以构造一种方案，先把$[i+1,k]$和$[k+1,j]$合并，再把$[i+1,j]$和$[i,i]$合并，贡献就是：
$g_{i,j}^{\prime }=g_{i+1,k}+g_{k+1,j}+w_{i+1,j}+w_{i,j}$

对比$g_{i,j}$和这个式子：
$g_{i,j}=g_{i+1,k}+w_{i,k}+g_{k+1,j}+w_{i,j}$
$g_{i,j}^{\prime }=g_{i+1,k}+w_{i+1,j}+g_{k+1,j}+w_{i,j}$

若$w_{i,k}\le w_{i+1,j}$：
则显然，$g_{i,j}\ge g_{i,j}^{\prime }$，则说明$i$也是最优决策点（由于假设$g_{i,j}$），与反论题矛盾.

否则：$w_{i,k}>w_{i+1,j}$
即：$a_i>w_{k+1,j}$

（说明右侧所有石子的大小加起来还没有$a_i$大）
此时我们构造一种方案：

先把$[i,k]$合并好，$[k+1,j]$区间保留原始的样子，然后把右侧的石子依次逐个加入左边的堆中，这种方案的总贡献为：
$g_{i,j}^{\prime \prime }=g_{i,k}+\left(\stackrel{j-1}{\sum _{t=k+1}}{w}_{i,t}\right)+w_{i,j}\ge g_{i,k}+(j-k-1)\cdot a_i+w_{i,j}>g_{i,k}+(j-k-1)\cdot w_{k+1,j}+w_{i,j}$

而我们知道$g$函数也像$f$一样具有上界：
$g_{k+1,j}\le (j-k-1)\cdot w_{k+1,j}$

因此：
$g_{i,j}^{\prime \prime }>g_{i,k}+(j-k-1)\cdot w_{k+1,j}+w_{i,j}\ge g_{i,k}+g_{k+1,j}+w_{i,j}=g_{i,j}$

此时，$g_{i,j}^{\prime \prime }>g_{i,j}$，证明新方案严格优于原方案，说明$k$不是最优决策点，矛盾。

大概意思就是说，对于区间$[i,k]$的最优决策点在其左端的情况，假如说$w_{i,k}\le w_{i+1,j}$，则$[i,j]$的左端点必然为最优决策点，矛盾。否则，$[i,j]$的右端点比$k$更优，$k$不为最优决策点，矛盾。

同理可证明，当区间$[k+1,j]$的最优决策点在其右端取得时，也会产生矛盾。

因此，根据现在的证明，在反论题成立的情况下，区间$[i,k]$的最优决策点为其右端点，而区间$[k+1,j]$的最优决策点为其左端点。

接下来证明这种情况不存在。

我们讨论区间$[i,k]$和区间$[k+1,j]$：
我们已经知道了$[i,k]$的最优决策点是$k$：
$g_{i,k}=g_{i,k-1}+w_{i,k}$
同理我们知道$[k+1,j]$的最优决策点是$k+1$：
$g_{k+1,j}=g_{k+2,j}+w_{k+1,j}$

总的贡献是：
$g_{i,j}=g_{i,k}+g_{k+1,j}+w_{i,j}=g_{i,k-1}+w_{i,k}+g_{k+2,j}+w_{k+1,j}+w_{i,j}$

这时候我们再构造另一种方案，先把$[k,k]$合并到$[i,k-1]$中，然后再把$[k+1,k+1]$加入到$[i,k]$中，最后再把$[i,k+1]$和$[k+2,j]$合并，这样做的贡献是：
$g_{i,j}^{\prime }=2\cdot g_{i,k-1}+w_{i,k}+w_{i,k+1}+g_{k+2,j}+w_{k+2,j}+w_{i,j}=2\cdot g_{i,k-1}+2\cdot w_{i,k}+g_{k+2,j}+w_{k+1,j}+w_{i,j}\ge g_{i,j}$

因为有假设最优决策点是$k$，就会有$g_{i,j}\ge g_{i,j}^{\prime }$，因此$g_{i,j}=g_{i,j}^{\prime }$。
这样就说明$k-1$这个位置也是最优决策点。
同理说明$k-2$也是最优决策点…说明$k-3$也是最优决策点…因此说明$i$是区间$[i,j]$最优决策点。与假设矛盾。

*注意这里证明左端点是最优决策点是为了导出矛盾，是在说明在反论题成立的情况下，这种情况不存在，而不是真的说明左端点永远是最优决策点。
（其实这时候甚至能证明出区间中的每一个点都是最优决策点。但是我们的假设是“假定两端不是最优决策点”，因此只要证出来两端是最优决策点就矛盾了）

因此反论题为假命题。

QED.

一种说法是$g_{i,j}$的最优决策点一定取自$a_i,a_j$中较小的那一端，这种说法是错误的。

题解视频

简单四边形不等式优化dp（下）