随着浙大mpa项目2024年提前批面试申请的截止，最新的申请人数也基本确定下来，从目前的信息来看，今年的提面申请数量与去年基本持平，很可能意味着今年的最终报考以及后续复试相关的一系列问题都可以去年为参考，这样一来，对于项目的报考形势也进一步清晰。

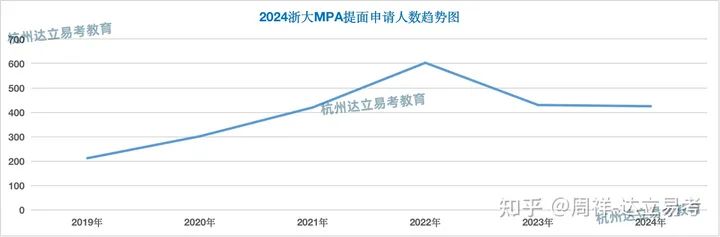浙大mpa项目提面申请人数

       杭州达立易考教育认为提前批面试的申请一般可以作为一个项目当年申请趋势的风向标。从浙大mpa项目的报考趋势可以看出今年的整体需求还是相对旺盛，去年提面申请在430人上下，而最终十月份网上报考量达到了1923人，创造历史之最，也是浙大mpa项目近些年录取最卷的一年，这还是在提前批面试拟录取人数严格限制的前提下，最高100个A的政策也决定了今年的总体资格率不超过25%，已经申请了的考生达立易考建议在接下来一个月时间内要抓紧时间备考，争取比例并不高的A资格机会。

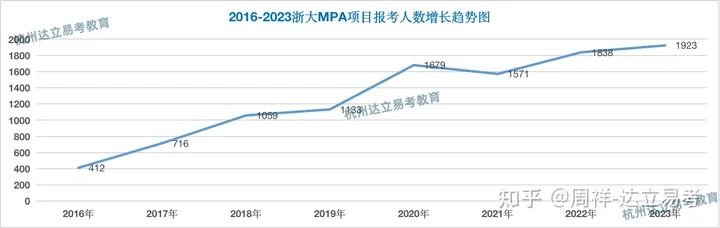浙大mpa项目报考人数

       从政策和实际角度来说，B资格每年会有部分考生递补到A资格录取，但却充满不确定性因素，比如A资格考生的过线率会直接影响到递补的名额，其次B资格本身所参加报考的人数以及过线率也会影响到递补的最终名次结果，因此对于浙大mpa提面的考生来讲，杭州达立易考教育认为最为稳妥的就是努力冲刺A资格，其次就是拿到B资格的高分次序，这样才能够有更大的几率获得国家线录取的资质，否则就要跟随常规批复试考生一同进入到第二阶段的面试竞争中。

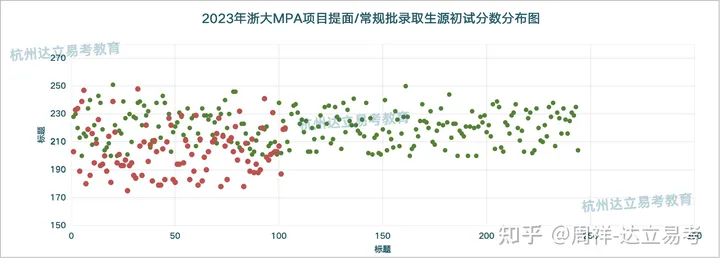浙大mpa提面常规批考生分数

       今年的面试将于10月中旬正式开启，不出意外的话将会采取现场面试的形式进行，距离目前的时间只有一个月，考生需要做的准备其实是比较多且广泛的，比如英语的备考就包含了口语能力和专业英语能力，而政治理论与公共管理专业知识也是考核的重点模块，如果没有积累的情况下达立易考教育认为是很难应对正式的面试的，因为最终结果的给定不是以背景打分，而是真真切切的依靠现场的沟通与应变能力，这一点是需要考生们关注且重视的。

       当然，在提面准备的同时，联考笔试的备考也到了关键时期，有限的备考时间内，除了踏踏实实的努力付出之外，复习的技巧与针对性也是取胜的关键所在！杭州达立易考预祝广大在职考生今年都可以顺利圆梦！（专注浙大 杭州达立易考）