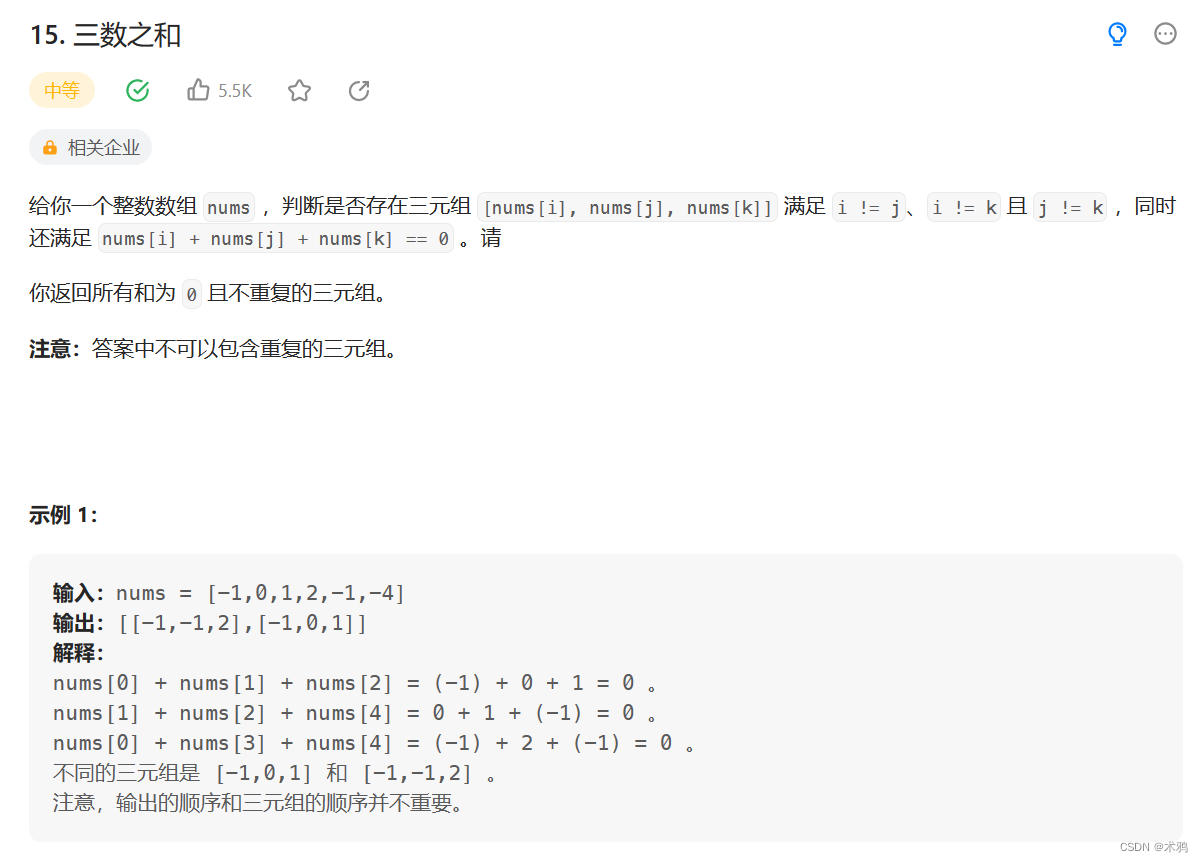
题目描述如上

要点分析：

遍历出所有的情况不难，难的是如果和处理重复的结果

纯暴力＋检索的话复杂度为n3，最后面的三个测试点会超时

所以这里使用双指针法进行处理，复杂度会变为n2

算法分析：

为了避免重复的结果，我们先把数组进行由低到高的排序，然后准备三个指针i，l，r

（1.减少遍历次数）先确定其中一个数字i，再去分析l，r的双指针移动情况，当和小于零的时候，可以让l右侧移动，反之就是r向左侧移动，这样的复杂度为n2

（2.减少重复解的方法）比如 l目前指向的是-1，但是l的下一位还是-1，下下位才是0，这样l再移动的时候不需要一个一个移动了，我们直接移动到下一个不同的数字上即可，

（3）具体的算法思路如下

1.先把数组从从小到大进行排列，然后设置固定位置i，左指针l=i+1，右指针r=size-1；

如果l<r,就代表当前i的条件下，情况还没有穷尽

如果目前的和小于零，左指针移动到下一个数字上

如果目前的和大于零，做指针移动到上一个数字上

如果目前和为0，就进行一下记录，然后这两个指针随便选一个移动

（注意移动的时候注意不能超过界限）

一旦到达了界限情况，r==l，代表这个i所在的情况已经穷尽了，我们要移动i（i的移动方法也是一样，在不越界的前提下，移动到下一个数字）然后根据i重置l和r

具体代码如下，成绩中等

vector<vector<int>> threeSum(vector<int>& nums) {
  vector<vector<int>> vvi;
    sort(nums.begin(), nums.end());
   int i=0;
   int l=i+1;
   int r=nums.size()-1;
   //另一种输入不符合的情况
    if(nums[i]>0||nums[r]<0||r<2){return vvi;}
   int num;
   while(l<r){
       num=nums[i]+nums[l]+nums[r];
       if(num>0){
           do{r--;}while(l<r && nums[r]==nums[r+1]);
       }else if(num<0){
           do{l++;}while(l<r && nums[l-1]==nums[l]);
       }else{
           vvi.push_back({nums[i],nums[l],nums[r]});
           do{l++;}while(l<r && nums[l-1]==nums[l]);
           
       }
       //补充的情况:1
       if(l==r&&l!=i+1){
           do{i++;}while(i+1<r && nums[i-1]==nums[i]);
           l=i+1;
           r=nums.size()-1;
       }
   }
    return vvi;
}