⛄一、数字图像处理简介
图像处理基础教程链接
1 【基础教程】基于matlab图像处理(表示方法+数据结构+基本格式+类型转换+读取+点运算+代数运算)【含Matlab源码 834期】
2 【基础教程】基于matlab图像处理(读写+显示+运算+转换+变换+增强+滤波+分析+统计)【含Matlab源码 144期】
3 【基础教程】基于matlab图像增强+复原+分割【含Matlab源码 056期】
⛄二、部分源代码
clear all;
close all;
i=imread(‘yanjing.bmp’);
imshow(i);
iii=i;
%把输入图象二值化,用canny算法返回阈值
sigma=3.0;
thresh=[0.03,0.09];
bw_1=i>70;
edgerm=edge(bw_1,‘canny’,thresh,sigma);
figure,imshow(edgerm);
t1=280;
s=0;
while t1>10
t2=1;
while t2<310
%查找第一个边缘点
if edgerm(t1,t2)1
u1=t1;
u2=t2;
s=1;
end
if s1
break;
end
t2=t2+1;
end
t1=t1-1;
end
po=1;
sum2=0;
%第一个边缘点
o1=u1;
o2=u2;
hang=zeros(0,0);
lie=zeros(0,0);
while (po1)
while (po1)
sum1=0;
for t3=1:5
for t4=1:5
% 第一个边缘点的左上方5个像素内有边缘点
if edgerm(u1-t3+1,u2+t4-1)1
% 第一个边缘点周围的边缘点个数
sum1=sum1+1;
sum2=sum2+1;
% 第sum1个边缘点位置x
hang(sum1,1)=u1-t3+1;
% 第sum1个边缘点位置y
hang(sum1,2)=u2+t4-1;
lie(sum2,1)=u1-t3+1;
lie(sum2,2)=u2+t4-1;
end
end
end
% 边缘点只有一个
if sum11
po=0;
% 没有边缘点
elseif sum10
po=0;
else
% 以最后的边缘点为起点,进行下一轮搜索
u1=hang(sum1,1);
u2=hang(sum1,2);
po=1;
end
end
% 边缘点个数小于30个
if sum2<30
u1=o1;
u2=o2+1;
po=1;
sum2=0;
% 横坐标不变,改变纵坐标值得到边缘点
while (edgerm(u1,u2)~=1)
while (edgerm(u1,u2)~=1)&(u2<310)
% 不是边缘点,纵坐标加1
u2=u2+1;
end
% 没有得到边缘点
if u2310
u1=u1-1;
u2=1;
end
end
% x不变,改变y重新得到边缘点
o1=u1;
o2=u2;
else
break;
end
end
% 边缘点个数
a1=size(lie);
w1=lie(a1(1),1);
w2=lie(a1(1),2);
po1=1;
while (po1==1)
sum1=0;
for t1=1:3
for t2=1:5
% 边缘点向左方3个像素,上方5个像素
if edgerm(w1-t1+1,w2-t2+1)1
sum1=sum1+1;
sum2=sum2+1;
lie(sum2,1)=w1-t1+1;
lie(sum2,2)=w2-t2+1;
hang(sum1,1)=w1-t1+1;
hang(sum1,2)=w2-t2+1;
end
end
end
% 边缘点只有一个
if sum11
po1=0;
else
po1=1;
w1=hang(sum1,1);
w2=hang(sum1,2);
end
end
po2=1;
while (po2==1)
sum1=0;
for t1=1:7
for t2=1:15
if edgerm(w1+t1-1,w2-t2+1)1
sum1=sum1+1;
sum2=sum2+1;
lie(sum2,1)=w1+t1-1;
lie(sum2,2)=w2-t2+1;
hang(sum1,1)=w1+t1-1;
hang(sum1,2)=w2-t2+1;
end
end
end
if sum11
po2=0;
else
po2=1;
w1=hang(sum1,1);
w2=hang(sum1,2);
end
end
%不止一个边缘点
while (w1=lie(1,1))&(w2=lie(1,2))
sum1=0;
for t1=1:5
for t2=1:5
%向右向上5个像素搜索边缘点
if edgerm(w1+t1-1,w2+t2-1)==1
sum1=sum1+1;
sum2=sum2+1;
lie(sum2,1)=w1+t1-1;
lie(sum2,2)=w2+t2-1;
hang(sum1,1)=w1+t1-1;
hang(sum1,2)=w2+t2-1;
end
end
end
w1=hang(sum1,1);
w2=hang(sum1,2);
end
for t1=1:280
for t2=1:320
% 初始化Hough矩阵
e(t1,t2)=0;
end
end
% 边缘点个数
for t1=1:size(lie)
% 将是边缘点的位置设为1
e(lie(t1,1),lie(t1,2))=1;
end
%确定瞳孔的边缘的上下限
minl=320;
maxl=1;
minh=280;
maxh=1;
for t1=1:280
for t2=1:320
if (e(t1,t2)==1)&(t2<minl)
minl=t2;
end
if (e(t1,t2)==1)&(t2>maxl)
maxl=t2;
end
if (e(t1,t2)==1)&(t1<minh)
minh=t1;
end
if (e(t1,t2)==1)&(t1>maxh)
maxh=t1;
end
end
end
% 采用二值化的方法求得瞳孔的面积sum3
sum3=0;
t1=minh;
while t1<=maxh
t2=minl;
while t2<=maxl
if (bw_1(t1,t2)==0)
sum3=sum3+1;
end
t2=t2+1;
end
t1=t1+1;
end
% 得到瞳孔r1半径向上取整,sum3表示瞳孔的面积
r1=ceil(sqrt(sum3/pi));
% 向下取整 估算出瞳孔圆心x坐标
c(1,1)=floor((maxh-minh)/2+minh);
c(1,2)=ceil((maxl-minl)/2+minl);
r2=ceil(r1/3);
r3=2r2;
for t1=1:ceil(r1/6)2
for t2=1:ceil(r1/6)2
pu(t1,t2)=0;
end
end
%pu中存放有相同圆心点的个数,以下找一个最大的pu认为是瞳孔的圆心
t1=minh;
while t1<=maxh
t2=minl;
while t2<=maxl
if (e(t1,t2)==1)
for a=1:2ceil(r1/6)
for b=1:2ceil(r1/6)
if (((t1-(c(1,1)+ceil(r1/6)-a))2+(t2-(c(1,2)-ceil(r1/6)+b))2-r12)>-10)&(((t1-(c(1,1)+ceil(r1/6)-a))2+(t2-(c(1,2)-ceil(r1/6)+b))2-r12)<10)
% 以a,b为圆心的圆累加个数
pu(a,b)=pu(a,b)+1;
end
end
end
end
t2=t2+1;
end
t1=t1+1;
end
ma=pu(1,1);
% 选取同心圆最多的圆心
for a=1:2ceil(r1/6)
for b=1:2*ceil(r1/6)
if (ma<pu(a,b))
ma=pu(a,b);
row=a;
col=b;
end
end
end
% 圆心坐标
c(1,1)=c(1,1)+ceil(r1/6)-row;
c(1,2)=c(1,2)-ceil(r1/6)+col;
j=double(i);
for t1=1:280
for t2=1:320
%虹膜内边缘设为白色
if ((t1-c(1,1))2+(t2-c(1,2))2-r12<80)&((t1-c(1,1))2+(t2-c(1,2))2-r12>-80)
i(t1,t2)=255;
end
end
end
row1=c(1,1);
col1=c(1,2);
%以上找到圆心(row1,col1),半径r1;
ha=row1;
li=col1;
sh1=1;
zong=0;
while sh1<=3
sh2=1;
while sh2<=3
zong=zong+1;
% 圆心向左、不变、向右移动2
row1=ha-4+sh12;
col1=li-4+sh22;
j1=double(i);
u=zeros(0,0);
for t1=1:row1
t2=col1;
while t2<=310
%第一像限的图像对角变换
u(row1-t1+1,t2-col1+1)=j1(t1,t2);
t2=t2+1;
end
end
u1=double(u);
%第一像限图像的行列数
yy=size(u);
%瞳孔半径r1
rr=r1+40;
l1=r1+40;
l2=1;
ll1=0;
n1=l1;
sq1=0;
%yy(1,2)表示第一像限的矩阵列数,yy(1,1)行数
while (l2<l1)&(l1<yy(1,2))&(l2<yy(1,1))
pk=(l1-1/2)2+(l2+1)2-rr^2;
%半径在rr+40范围内
if pk<0
%沿着l1方向灰度值累加
sq1=sq1+u1(l2+1,l1);
%记录sql的个数
ll1=ll1+1;
l1=l1;
l2=l2+1;
else sq1=sq1+u1(l2+1,l1-1);
ll1=ll1+1;
l1=l1-1;
l2=l2+1;
end
end
⛄三、运行结果
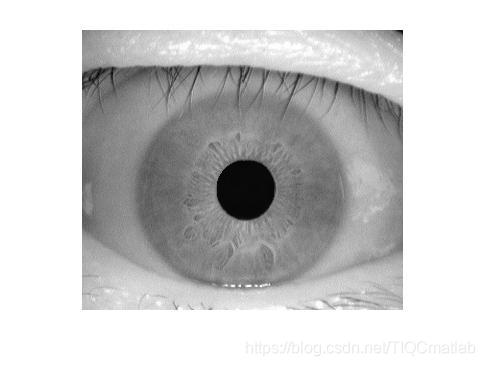
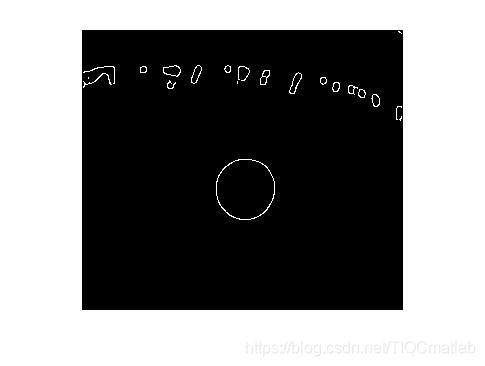


⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]朱琼瑶.结合人眼特征和几何方法的虹膜定位方法[J].计算机工程与应用. 2013,49(08)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除